Ex 6.5,22

Transcript

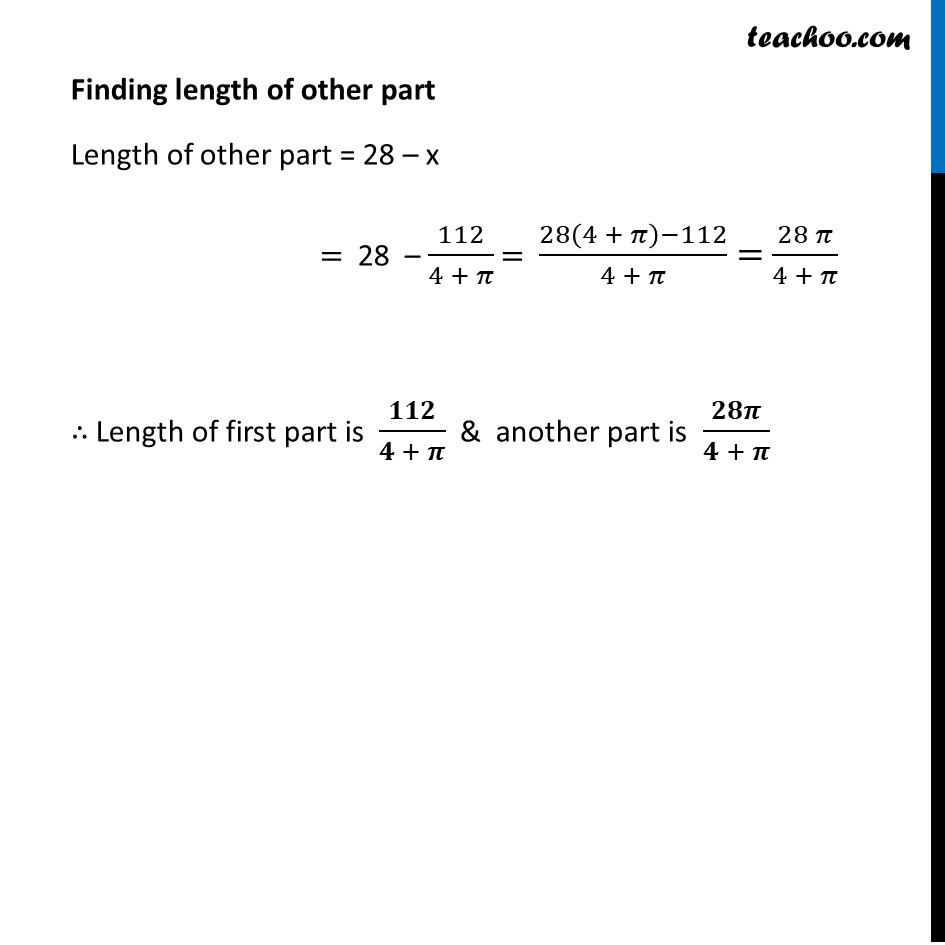
Ex 6.5,22 A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum? A wire of length 28m cut into two parts Let 𝑥 be the length of first part Length of 2nd part = 28−𝑥﷯𝑚 Given that one part is converted into a square Let length of 𝑥 m be converted into a square Thus, Perimeter of square =𝑥 4 𝑠𝑖𝑑𝑒 𝑜𝑓 𝑠𝑞𝑢𝑎𝑟𝑒 ﷯=𝑥 side of square of = 𝑥﷮4﷯ Also, other part is converted into Circle ⇒ 28−𝑥﷯ m length converted into a Circle of radius 𝑟 Circumference of circle = 28−𝑥﷯ m 2𝜋𝑟= 28−𝑥﷯ 𝑟= 28 − 𝑥﷮2𝜋﷯﷯ m We need to find length of pieces so that the combined Area of Circle & Square is minimum Let T be the total area of circle & square T = Area of Circle + Area of Square T = 𝜋 𝑟﷮2﷯+ 𝑠𝑖𝑑𝑒﷯﷮2﷯ T = 𝜋 28 − 𝑥﷮2𝜋﷯﷯﷮2﷯+ 𝑥﷮2﷯﷮16﷯ We have to minimize T Diff T w.r.t 𝑥 𝑑𝑇﷮𝑑𝑥﷯= 𝑑﷮𝑑𝑥﷯ 28 − 𝑥﷯﷮2﷯﷮4𝜋﷯+ 𝑥﷮2﷯﷮16﷯ ﷯ = 2 28 − 𝑥﷯﷮4𝜋﷯ . 𝑑 28 − 𝑥﷯﷮𝑑𝑥﷯+ 2𝑥﷮16﷯ = 28 − 𝑥﷮2𝜋﷯ −1﷯+ 𝑥﷮8﷯ = 𝑥 − 28﷮2𝜋﷯+ 𝑥﷮8﷯ Putting 𝑑𝑇﷮𝑑𝑥﷯=0 𝑥 − 28﷮2𝜋﷯+ 𝑥﷮8﷯=0 4 𝑥 − 28﷯ + 𝜋𝑥﷮8𝜋﷯ =0 4x – 112 +𝜋 𝑥=0×8 𝜋 𝑥 4+𝜋﷯=112 𝑥= 112﷮4 + 𝜋﷯ Now finding 𝑑﷮2﷯𝑇﷮𝑑 𝑥﷮2﷯﷯ 𝑑𝑇﷮𝑑𝑥﷯= −28 + 𝑥﷮2𝜋﷯+ 𝑥﷮8﷯ 𝑑﷮2﷯𝑇﷮𝑑 𝑥﷮2﷯﷯= 1﷮2𝜋﷯ 0+1﷯+ 1﷮8﷯ 𝑑﷮2﷯𝑇﷮𝑑 𝑥﷮2﷯﷯= 1﷮2𝜋﷯+ 1﷮8﷯ > 0 Hence 𝑑﷮2﷯𝑇﷮𝑑 𝑥﷮2﷯﷯>0 at 𝑥= 112﷮4 + 𝜋﷯ ⇒ Total area is Minimum at 𝑥 = 112﷮4 + 𝜋﷯ Finding length of other part Length of other part = 28 – x = 28 – 112﷮4 + 𝜋﷯ = 28 4 + 𝜋﷯−112﷮4 + 𝜋﷯= 28 𝜋﷮4 + 𝜋﷯ ∴ Length of first part is 𝟏𝟏𝟐﷮𝟒 + 𝝅﷯ & another part is 𝟐𝟖𝝅﷮𝟒 + 𝝅﷯