Ex 7.3, 5 - Chapter 7 Class 12 Integrals

Transcript

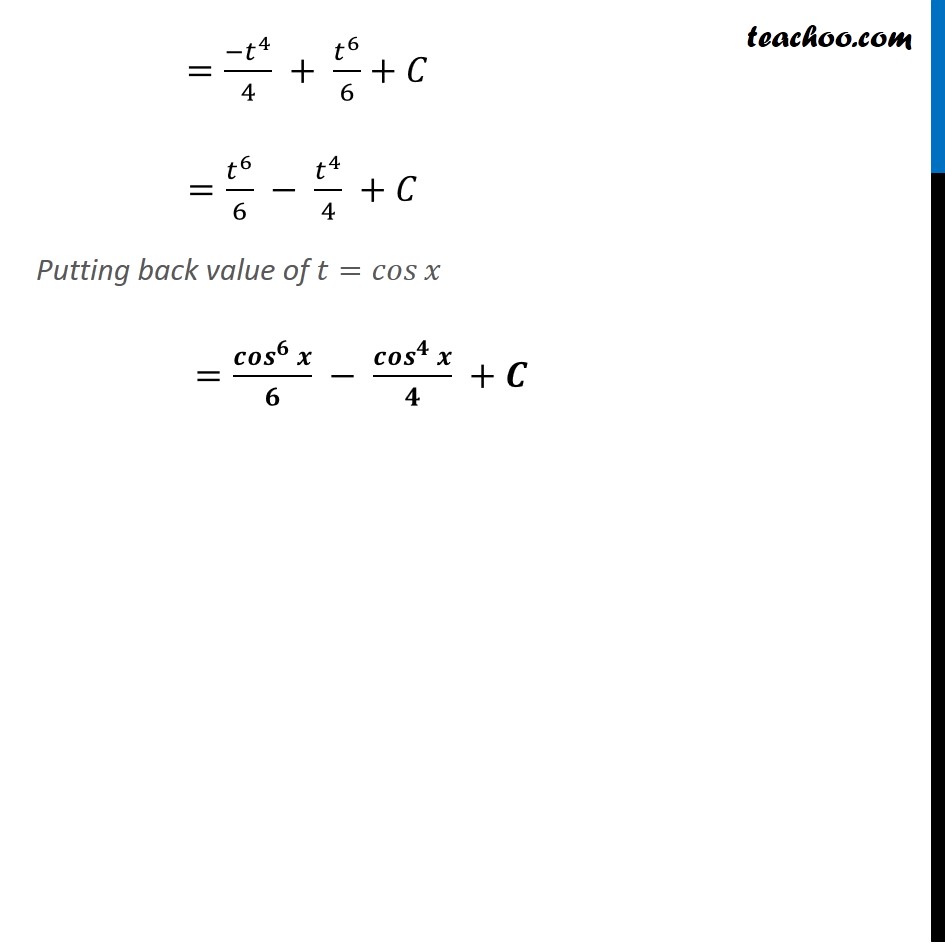
Ex 7.3, 5 Integrate sin^3⁡𝑥 cos^3 𝑥 ∫1▒〖sin^3⁡𝑥 cos^3 𝑥〗 𝑑𝑥 =∫1▒〖𝑠𝑖𝑛⁡𝑥. sin^2⁡𝑥 cos^3 𝑥〗 𝑑𝑥 =∫1▒〖𝑠𝑖𝑛⁡𝑥 (1−cos^2⁡𝑥 ) cos^3 𝑥〗 𝑑𝑥 =∫1▒〖(1−cos^2⁡𝑥 ) cos^3 𝑥〗. 𝑠𝑖𝑛⁡𝑥 𝑑𝑥 Let cos⁡𝑥=𝑡 Differentiating w.r.t.x −sin⁡𝑥=𝑑𝑡/𝑑𝑥 𝑑𝑥=𝑑𝑡/(−sin⁡𝑥 ) (〖𝑠𝑖𝑛〗^2⁡𝜃=1−〖𝑐𝑜𝑠〗^2⁡𝜃) …(1) Thus, our equation becomes ∫1▒〖sin^2⁡𝑥 cos^3 𝑥〗 𝑑𝑥 =∫1▒〖(1−cos^2⁡𝑥 ) cos^3 𝑥〗. 𝑠𝑖𝑛⁡𝑥 𝑑𝑥" " =∫1▒〖(1−𝑡^2 ) 𝑡^3 〗. 𝑠𝑖𝑛⁡𝑥×1/(−sin⁡𝑥 ) 𝑑𝑡" " =∫1▒〖−(1−𝑡^2 ) 𝑡^3 〗 𝑑𝑡" " =−∫1▒〖(𝑡^3−𝑡^5 ) 〗 𝑑𝑡" " =−[∫1▒𝑡^3 𝑑𝑡−∫1▒𝑡^5 𝑑𝑡] =−[𝑡^(3 + 1)/(3 + 1) − 𝑡^(5 + 1)/(5 + 1)]+𝐶 =−[𝑡^4/4 − 𝑡^6/6]+𝐶 =〖−𝑡〗^4/4 + 𝑡^6/6+𝐶 =𝑡^6/6 − 𝑡^4/4 +𝐶 Putting back value of 𝑡=𝑐𝑜𝑠⁡𝑥 =(〖𝒄𝒐𝒔〗^𝟔 𝒙)/𝟔 − (〖𝒄𝒐𝒔〗^𝟒 𝒙)/𝟒 +𝑪