Example 31 - Chapter 6 Class 12 Application of Derivatives
Last updated at Dec. 16, 2024 by Teachoo
Examples
Example 1
You are here
You are here
Transcript
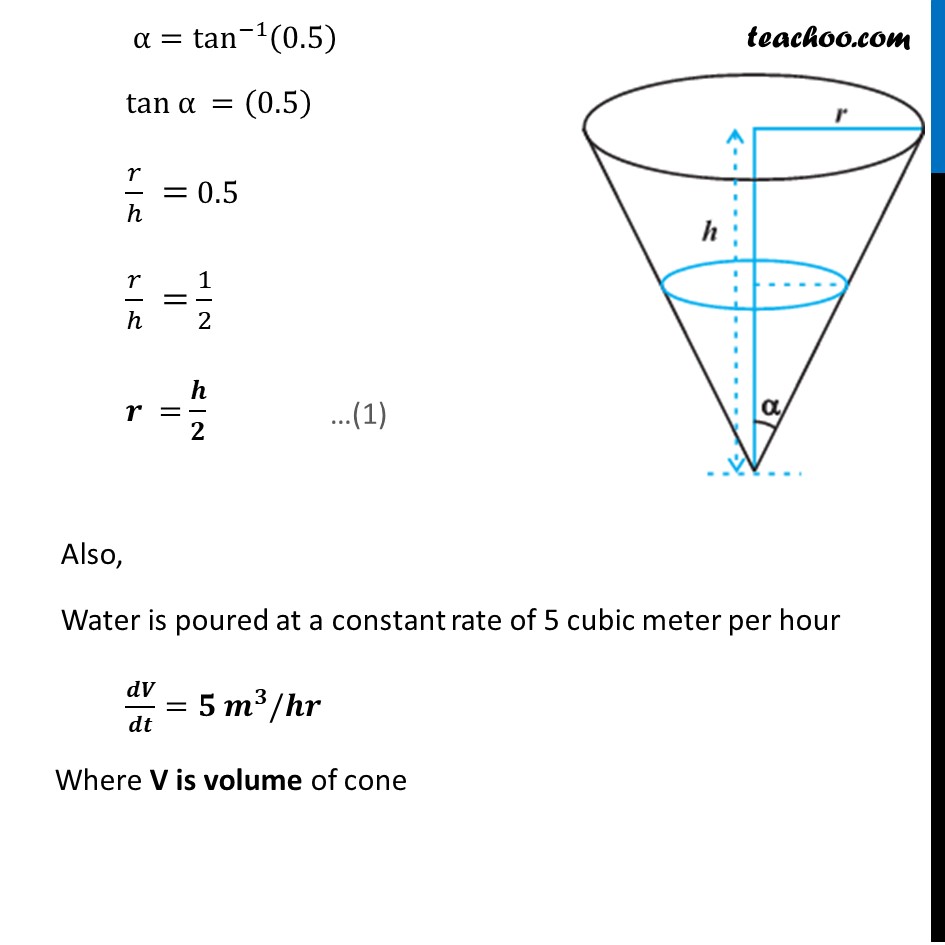
Example 31 A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tanβ1 (0.5). Water is poured into it at a constant rate of 5 cubic meter per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4 m.Water tank is in shape of cone Let r be the radius of cone, h be the height of cone, & πΆ be the semiβvertical angle Given Semi-vertical angle is tan^(β1)β‘(0.5) Ξ±=tan^(β1)β‘(0.5) tan Ξ± =(0.5) π/β = 0.5 π/β = 1/2 π = π/π Also, Water is poured at a constant rate of 5 cubic meter per hour π π½/π π=π π^π/ππ Where V is volume of cone Now, π=1/3 ππ^2 β π=1/3 π(π/π)^2 β π=1/3 π(γh/4γ^2 )β π½=(π π^π)/ππ Differentiate w.r.t. t ππ/ππ‘=π((πβ^3)/12)/ππ‘ ππ/ππ‘=π/12 . (πβ^3)/ππ‘ ππ/ππ‘=π/12 . (πβ^3)/πβ .πβ/ππ‘ ππ/ππ‘=π/12. 3β^2 . πβ/ππ‘ ππ/ππ‘=(πβ^2)/4 . πβ/ππ‘ Putting π π½/π π=π 5 =(πβ^2)/4 . πβ/ππ‘ π π/π π=ππ/(π π^π ) We need to find, Rate at which level of water is rising when depth is 4 m i.e. β π π/π πβ€|_(π = π π) Putting h = 4 m in (3) β πβ/ππ‘β€|_(β = 4π)=20/(π(β)^2 )=20/16 Γ 1/π=5/4 Γ 1/(22/7)=5/4 Γ 7/22=35/88 Hence, rate of change of water level is ππ/ππ m/hr.
