Example 29 - Chapter 6 Class 12 Application of Derivatives

Transcript

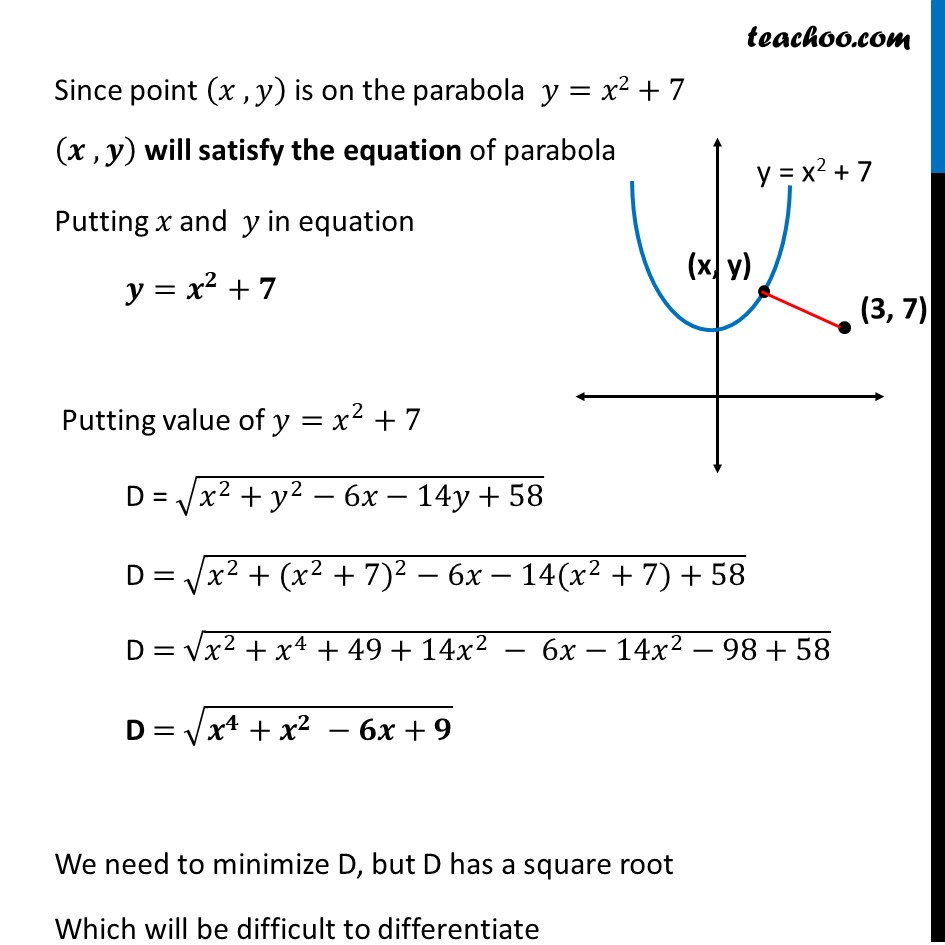
Example 29 An Apache helicopter of enemy is flying along the curve given by 𝑦= 𝑥^2 + 7. A soldier, placed at (3, 7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.Given curve y = x2 + 7 Let (𝑥,𝑦) be any point on parabola 𝑦=𝑥2+7 Let D be required Distance between (𝑥,𝑦) & (3 , 7) D = √((𝟑−𝒙)^𝟐+(𝟕 −𝒚)^𝟐 ) = √(9+𝑥^2−6𝑥+49+𝑦^2−14𝑦) = √(𝑥^2+𝑦^2−6𝑥−14𝑦+58) Since point (𝑥 , 𝑦) is on the parabola 𝑦=𝑥2+7 (𝒙 , 𝒚) will satisfy the equation of parabola Putting 𝑥 and 𝑦 in equation 𝒚=𝒙^𝟐+𝟕 Putting value of 𝑦=𝑥^2+7 D = √(𝑥^2+𝑦^2−6𝑥−14𝑦+58) D = √(𝑥^2+〖(𝑥^2+7)〗^2 − 6𝑥−14(𝑥^2+7)+58) D = √(𝑥^2+𝑥^4+49+14𝑥^2 − 6𝑥−14𝑥^2−98+58) D = √(𝒙^𝟒+𝒙^𝟐 −𝟔𝒙+𝟗) We need to minimize D, but D has a square root Which will be difficult to differentiate Let Z = D2 Z = 𝒙^𝟒+𝒙^𝟐 −𝟔𝒙+𝟗 Since D is positive, D is minimum if D2 is minimum So, we minimize Z = D2 Differentiating Z Z =𝑥^4+𝑥^2 −6𝑥+9 Differentiating w.r.t. h Z’ = 𝑑(𝑥^4 + 𝑥^2 − 6𝑥 + 9)/𝑑ℎ Z’ = 4𝑥^3+2𝑥 −6 Putting Z’ = 0 4𝑥^3+2𝑥 −6=0 Factorizing Z’ Z’(1) = 4(1)3 + 2(1) − 6 = 4 + 2 − 6 = 0 Hence, (x – 1) is a factor of 4x3 − 2x − 6 Thus, 4𝑥^3+2𝑥 −6=0 (𝑥−1)(4𝑥^2+4𝑥+6)=0 2x2 + 2x + 3 = 0 x = (−2 ± √(4 − 4(2)(3)))/4 = (−2 ± √(−𝟐𝟎))/4 This is not possible as there are no real roots. Checking sign of 𝒁^′′ " " 𝑑𝑍/𝑑𝑥=4𝑥^3+2𝑥 −6 Differentiating again w.r.t x (𝑑^2 𝑍)/(𝑑𝑥^2 )=4 × 3𝑥^2+2 (𝑑^2 𝑍)/(𝑑𝑥^2 )=12𝑥^2+2 Since 𝐙^′′ > 0 for x = 1 ∴ Z is minimum when x = 1 Thus, D is Minimum at x = 1 Finding Minimum value of D D = √(𝒙^𝟒+𝒙^𝟐 −𝟔𝒙+𝟗) Putting x = 1 D = √(1^4+1^2−6(1)+9) D = √𝟓 Hence, shortest distance is√𝟓