Example 26 - Chapter 6 Class 12 Application of Derivatives

Transcript

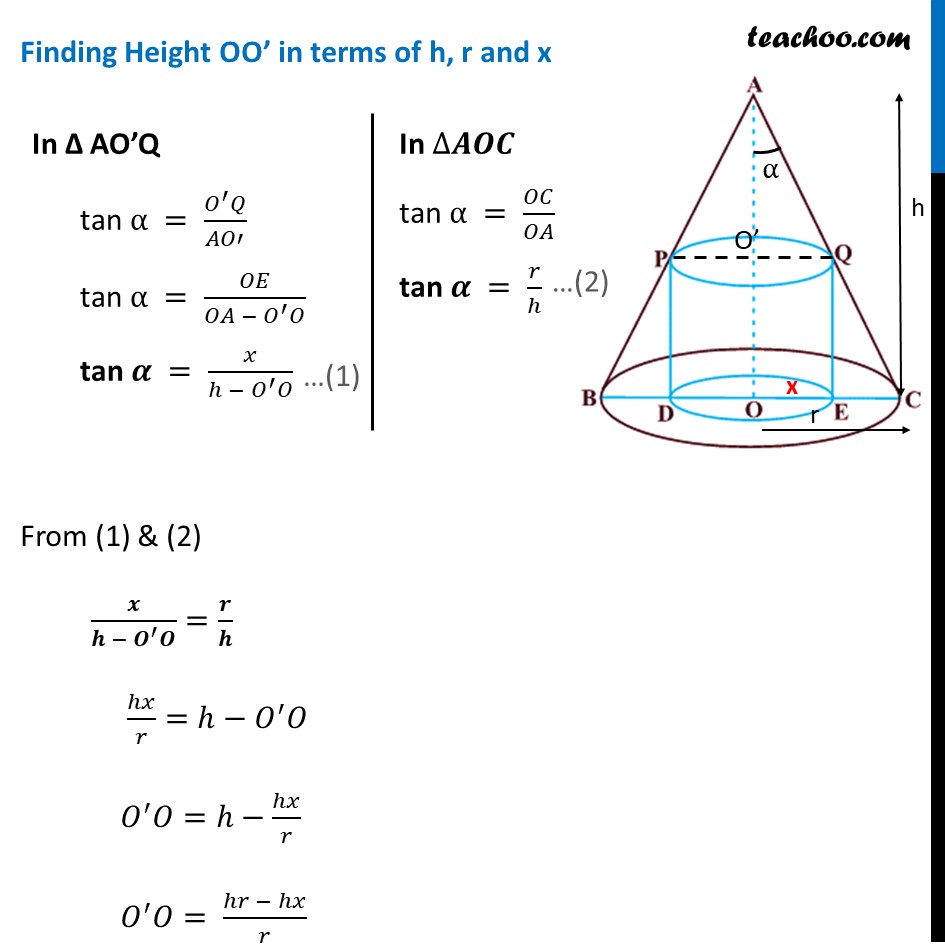
Example 26 Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that cone. Let OC = r be the radius of cone & OA = h be height of cone & ∠ OAQ = α be the semi-vertical angle of cone And, Let OE = x be the radius of cylinder Height of cylinder = OO’ Since cone is given, radius (r) and height (h) of cone are constant And, radius (x) and height (OO’) of cylinder is variable In Δ AO’Q tan α = (𝑂^′ 𝑄)/𝐴𝑂′ tan α = 𝑂𝐸/(𝑂𝐴 − 𝑂^′ 𝑂) tan 𝜶 = 𝑥/(ℎ − 𝑂^′ 𝑂) In ∆𝑨𝑶𝑪 tan α = 𝑂𝐶/𝑂𝐴 tan 𝜶 = 𝑟/ℎ Finding Height OO’ in terms of h, r and x From (1) & (2) 𝒙/(𝒉 − 𝑶^′ 𝑶)=𝒓/𝒉 ℎ𝑥/𝑟=ℎ−𝑂^′ 𝑂 𝑂^′ 𝑂=ℎ−ℎ𝑥/𝑟 𝑂^′ 𝑂= (ℎ𝑟 − ℎ𝑥)/𝑟 𝑶^′ 𝑶= 𝒉(𝒓 − 𝒙)/𝒓 Now, Curved Surface Area of Cylinder = 2𝜋 × Radius × Height S = 2𝜋" × " 𝑥" × " 𝑂^′ 𝑂 S = 2𝜋𝑥 ℎ(𝑟 − 𝑥)/𝑟 S = 2𝜋ℎ/𝑟 (𝑟𝑥−𝑥^2 ) S = 𝒌(𝒓𝒙−𝒙^𝟐 ) We need to minimize S Finding S’(x) S’ (x) = 𝑑(𝑘(𝑟𝑥 − 𝑥^2 ))/𝑑𝑥 S’ (x) = 𝑘 𝑑(𝑟𝑥 − 𝑥^2 )/𝑑𝑥 S’ (x) = 𝑘(𝑟−2𝑥) Putting S’ = 0 0 = 𝑘(𝑟−2𝑥) 𝑟−2𝑥 = 0 𝒙 = 𝒓/𝟐 Finding S’’(x) at x = 𝒓/𝟐 S’’ (x) = 𝑑(𝑘(𝑟 − 2𝑥))/𝑑𝑥 S’’ (x) = 𝑘 𝑑(𝑟 − 2𝑥)/𝑑𝑥 S’’ = 𝑘 (0−2) S’’ = −2𝑘 Therefore, S’’ (x) < 0 for 𝑥=𝑟/2 Thus, 𝒙=𝒓/𝟐 is maxima of S. Hence, radius of cylinder with greatest curved surface area which can be inscribed in a given cone is half of that cone