Example 23 - Chapter 6 Class 12 Application of Derivatives

Transcript

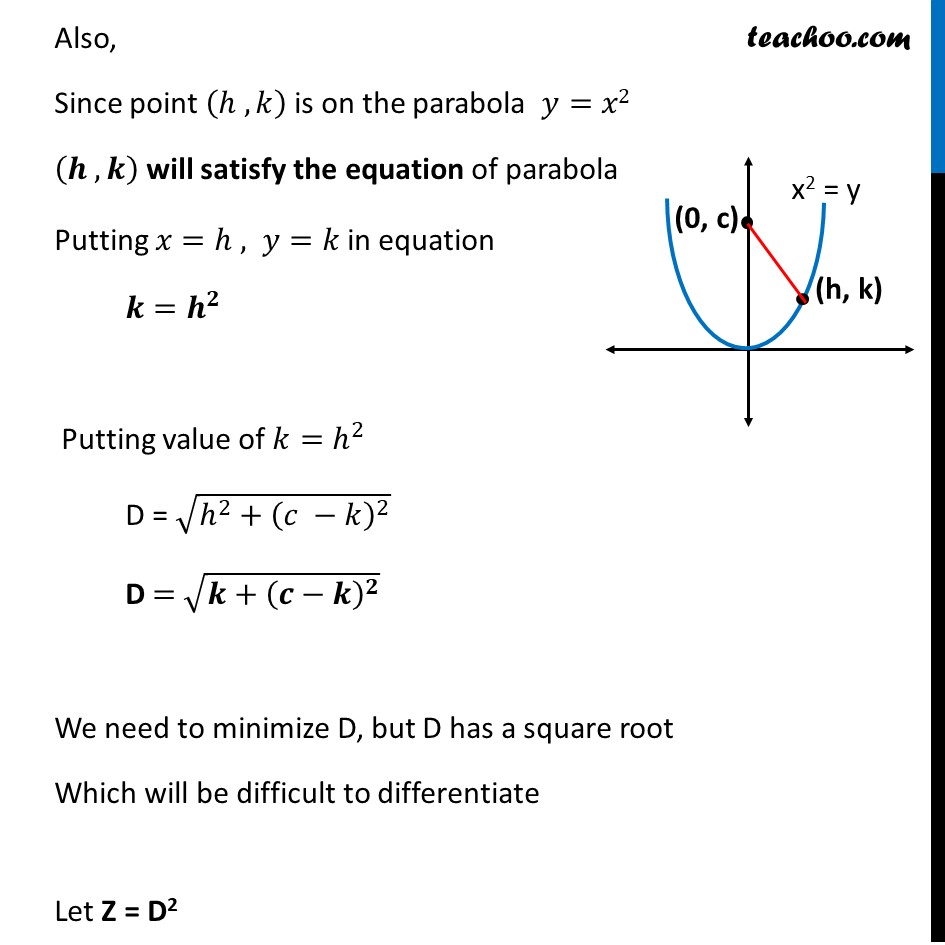
Example 23 Find the shortest distance of the point (0, c) from the parabola 𝑦=𝑥2, where 0 ≤ c ≤ 5. Let (ℎ ,𝑘) be any point on parabola 𝑦=𝑥2 Let D be required Distance between (ℎ , 𝑘) & (0 , 𝑐) D = √((0−ℎ)^2+(𝑐 −𝑘)^2 ) D = √((−ℎ)^2+(𝑐 −𝑘)^2 ) D = √(𝒉^𝟐+(𝒄 −𝒌)^𝟐 ) Also, Since point (ℎ , 𝑘) is on the parabola 𝑦=𝑥2 (𝒉 , 𝒌) will satisfy the equation of parabola Putting 𝑥=ℎ , 𝑦=𝑘 in equation 𝒌=𝒉^𝟐 Putting value of 𝑘=ℎ^2 D = √(ℎ^2+(𝑐 −𝑘)^2 ) D = √(𝒌+(𝒄−𝒌)^𝟐 ) We need to minimize D, but D has a square root Which will be difficult to differentiate Let Z = D2 Z = 𝑘+(𝑐−𝑘)^2 Since D is positive, D is minimum if D2 is minimum So, we minimize Z = D2 Differentiating Z Z =𝑘+(𝑐−𝑘)^2 Differentiating w.r.t. k Z’ = 𝑑(𝑘 + (𝑐 − 𝑘)^2 )/𝑑𝑘 Z’ = 1 + 2 (c − k) × (c − k)’ Z’ = 1 + 2 (c − k) × (0 − 1) Z’ = 1 − 2 (c − k) Z’ = 1 − 2c − 2k Putting Z’ = 0 1 − 2c − 2k = 0 2k = 2c − 1 k = (𝟐𝒄 − 𝟏)/𝟐 Now, checking sign of 𝒁^′′ " " 𝑑𝑍/𝑑𝑘=4𝑘−2𝑐 Differentiating again w.r.t k (𝑑^2 𝑍)/(𝑑ℎ^2 ) = 4 −0 (𝒅^𝟐 𝒁)/(𝒅𝒉^𝟐 ) = 𝟒 Since 𝐙^′′ > 0 for k = (2𝑐 − 1)/2 ∴ Z is minimum when k = (2𝑐 − 1)/2 Thus, D is Minimum at 𝒌=(𝟐𝒄 − 𝟏)/𝟐 Finding Minimum value of D D = √(𝑘+(𝑐−𝑘)^2 ) Putting 𝑘=(2𝑐 − 1)/2 D = √(((2𝑐 − 1)/2)+(𝑐−((2𝑐 − 1)/2))^2 ) D = √(((2𝑐 − 1)/2)+((2𝑐 − 2𝑐 − 1)/2)^2 ) D = √(((2𝑐 − 1)/2)+((−1)/2)^2 ) D = √(((2𝑐 − 1)/2)+1/4) D = √(𝑐−1/2+1/4) D = √(𝑐−1/4) D = √(4𝑐 − 1)/2 Hence, shortest distance is √(𝟒𝒄 − 𝟏)/𝟐