
Ex 5.1
Ex 5.1 ,2
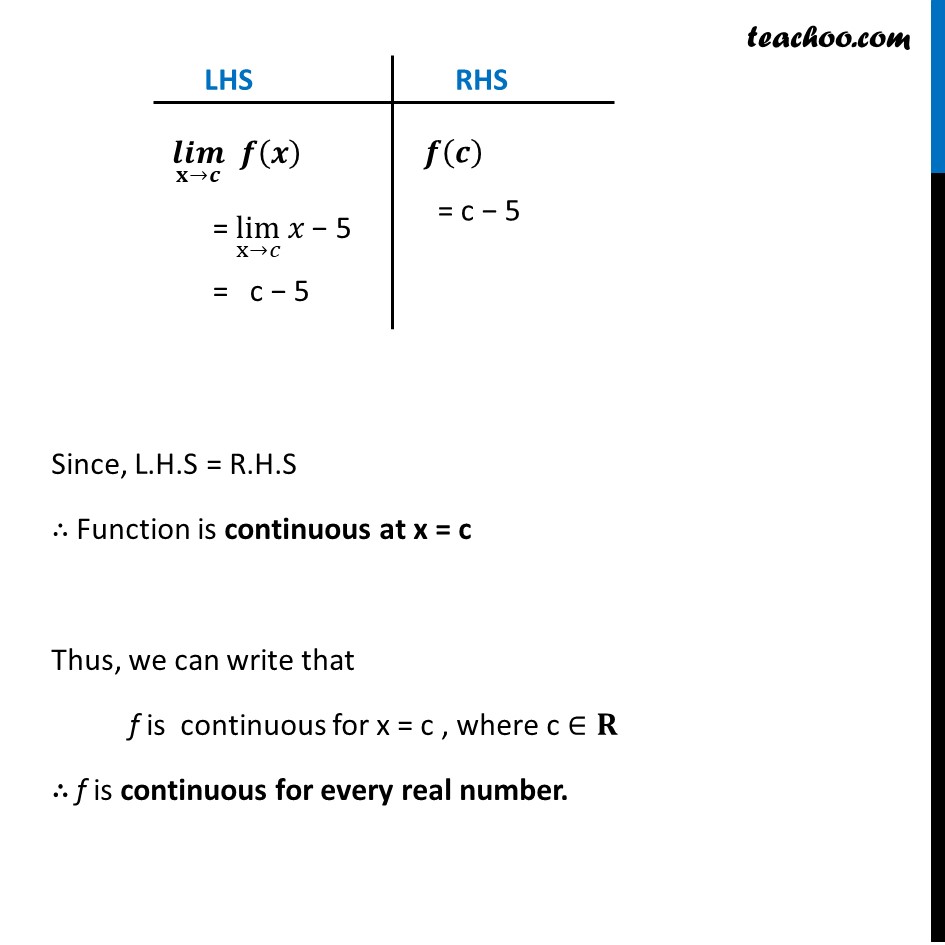
Ex 5.1, 3 (a) You are here
Ex 5.1, 3 (b)
Ex 5.1, 3 (c) Important
Ex 5.1, 3 (d) Important
Ex 5.1 ,4
Ex 5.1 ,5 Important
Ex 5.1 ,6
Ex 5.1 ,7 Important
Ex 5.1 ,8
Ex 5.1, 9 Important
Ex 5.1, 10
Ex 5.1, 11
Ex 5.1, 12 Important
Ex 5.1, 13
Ex 5.1, 14
Ex 5.1, 15 Important
Ex 5.1, 16
Ex 5.1, 17 Important
Ex 5.1, 18 Important
Ex 5.1, 19 Important
Ex 5.1, 20
Ex 5.1, 21
Ex 5.1, 22 (i) Important
Ex 5.1, 22 (ii)
Ex 5.1, 22 (iii)
Ex 5.1, 22 (iv) Important
Ex 5.1, 23
Ex 5.1, 24 Important
Ex 5.1, 25
Ex 5.1, 26 Important
Ex 5.1, 27
Ex 5.1, 28 Important
Ex 5.1, 29
Ex 5.1, 30 Important
Ex 5.1, 31
Ex 5.1, 32
Ex 5.1, 33
Ex 5.1, 34 Important
Last updated at April 16, 2024 by Teachoo


Ex 5.1, 3 Examine the following functions for continuity. (a) f(x) = x – 5 f(x) = x – 5 To check continuity of 𝑓(𝑥), We check it’s if it is continuous at any point x = c Let c be any real number f is continuous at 𝑥 =𝑐 if (𝐥𝐢𝐦)┬(𝐱→𝒄) 𝒇(𝒙)=𝒇(𝒄) (𝒍𝒊𝒎)┬(𝐱→𝒄) 𝒇(𝒙) = lim┬(x→𝑐) 𝑥 − 5 = c − 5 𝒇(𝒄) = c − 5 Since, L.H.S = R.H.S ∴ Function is continuous at x = c Thus, we can write that f is continuous for x = c , where c ∈𝐑 ∴ f is continuous for every real number.