Ex 9.3, 22 - Chapter 9 Class 12 Differential Equations

Transcript

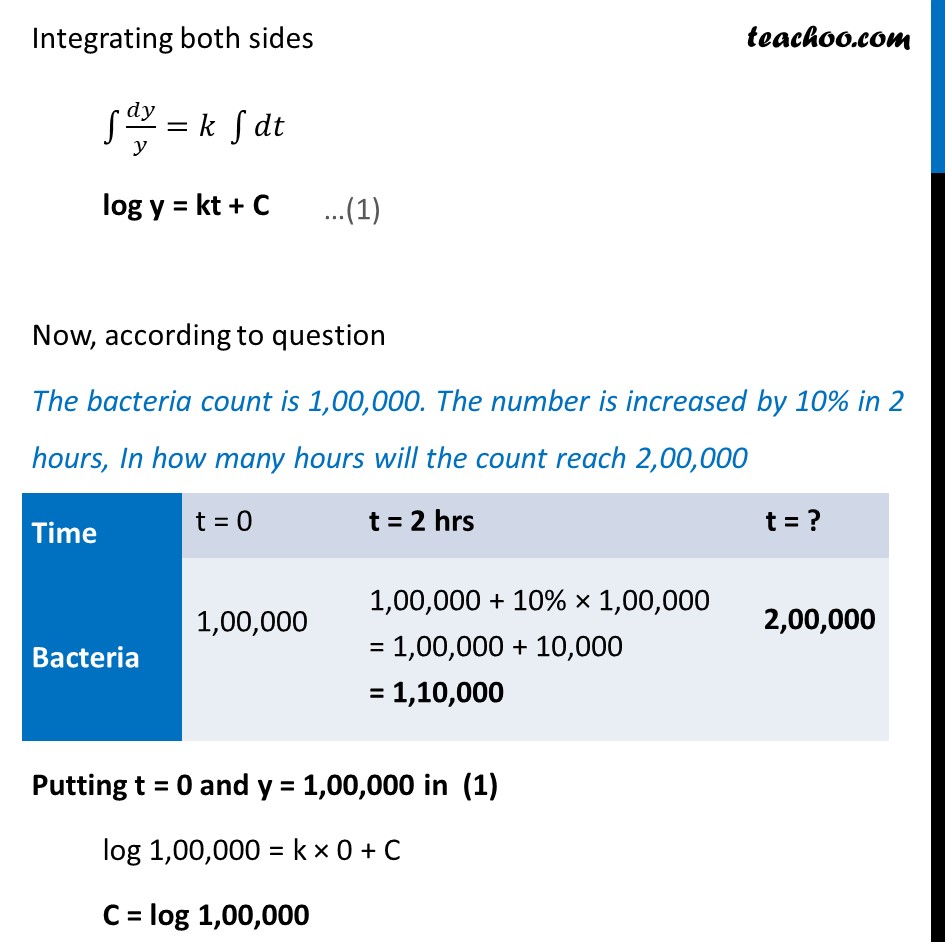
Ex 9.3, 22 In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours, In how many hours will the count reach 2,00,000 , if the rate of growth of bacteria is proportional to the number present? Let the number of bacteria at time t be y Given that rate of growth of bacteria is proportional to the number present 𝑑𝑦/𝑑𝑡 ∝ y 𝑑𝑦/𝑑𝑡 = ky 𝑑𝑦/𝑦 = kdt Integrating both sides ∫1▒〖𝑑𝑦/𝑦=𝑘〗 ∫1▒𝑑𝑡 log y = kt + C Now, according to question The bacteria count is 1,00,000. The number is increased by 10% in 2 hours, In how many hours will the count reach 2,00,000 Putting t = 0 and y = 1,00,000 in (1) log 1,00,000 = k × 0 + C C = log 1,00,000 …(1) Putting value of C in (1) log y = kt + C log y = kt + log 1,00,000 Now, Putting t = 2 and y = 1,00,000 in (2) log 1,10,000 = 2k + log 1,00,000 log 1,10,000 − log 1,00,000 = 2k log (1,10,000/1,00,000) = 2k 1/2 log (11/10) = k …(2) Putting value of k in (2) log y = kt + log 1,00,000 log y = 1/2 log (11/10) t + log 1,00,000 Now, If Bacterial = 2,00,000, we have to find t Putting y = 2,00,000 in (3) log 2,00,000 = 1/2 log (11/10) t + log (1,00,000) log 2,00,000 − log 1,00,000 = 1/2 log (11/10) t log (2,00,000/1,00,000) = 1/2 log (11/10) t log 2 = 1/2 log (11/10) t t = (𝟐 𝐥𝐨𝐠⁡𝟐)/𝐥𝐨𝐠⁡〖 (𝟏𝟏/𝟏𝟎)〗 …(3)