Ex 12.1, 21 - Chapter 12 Class 11 Limits and Derivatives

Transcript

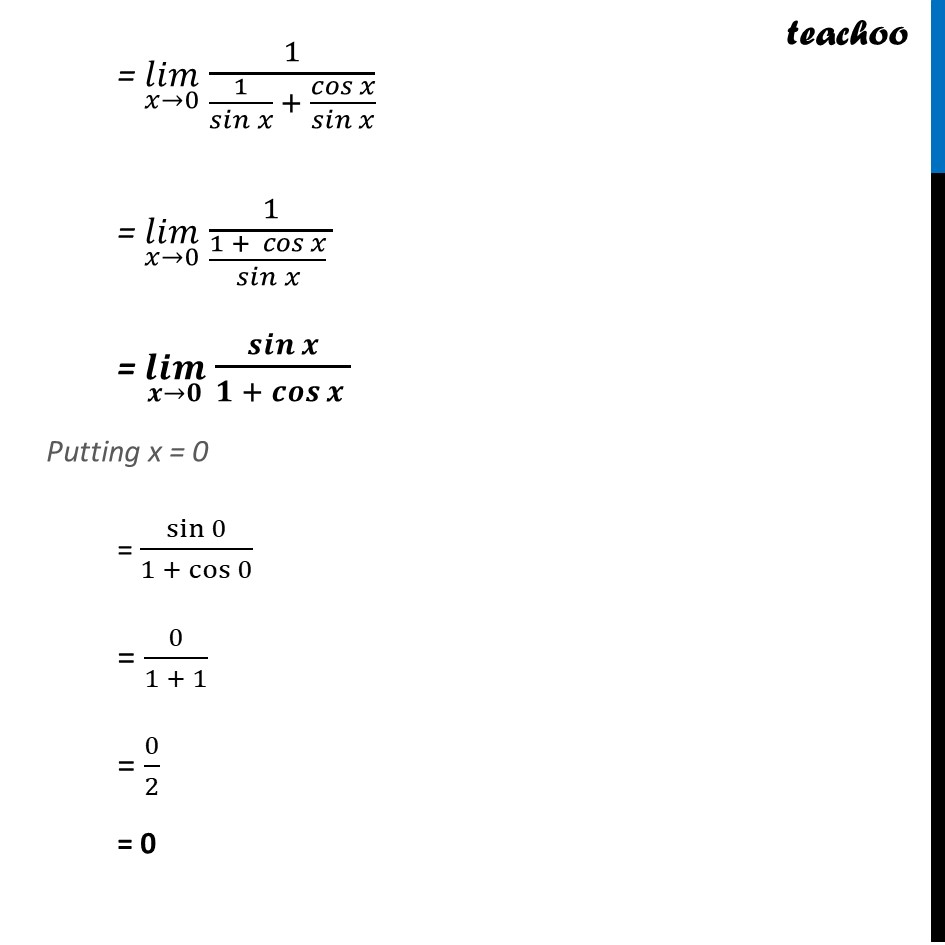
Ex 12.1, 21 (Method 1) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) lim┬(x→0) (cosec x – cot x) = lim┬(x→0) (1/sin⁡𝑥 −cos⁡𝑥/sin⁡𝑥 ) = lim┬(x→0) (1 −〖 cos〗⁡𝑥)/sin⁡〖𝑥 〗 Putting x = 0 = (1 − cos⁡〖0 〗)/sin⁡0 = (1 − 1)/0 = 0/0 Using cosec θ = (1 )/(sin θ) cot θ = (cos θ)/(sin θ) Since it is coming 0/0 Hence, we need to simplify lim┬(x→0) (1 −〖 cos〗⁡𝑥)/sin⁡〖𝑥 〗 = lim┬(x→0) (1 −〖 cos〗⁡𝑥)/sin⁡〖𝑥 〗 × (𝟏 + 𝐜𝐨𝐬⁡𝒙)/(𝟏 + 𝒄𝒐𝒔⁡𝒙 ) = lim┬(x→0) (1^2 −〖 cos^2〗⁡𝑥)/(sin⁡〖𝑥 〗 (1 + cos⁡𝑥 ) ) = lim┬(x→0) (𝟏 −〖 〖𝒄𝒐𝒔〗^𝟐〗⁡𝒙)/(sin⁡〖𝑥 〗 (1 + cos⁡𝑥 ) ) = lim┬(x→0) 〖 〖𝐬𝐢𝐧〗^𝟐〗⁡𝒙/(sin⁡〖𝑥 〗 (1 + cos⁡𝑥 ) ) = lim┬(x→0) 〖 𝑠𝑖𝑛〗⁡𝑥/((1 + cos⁡𝑥 ) ) Putting x = 0 = 〖 𝑠𝑖𝑛〗⁡0/((1 + cos⁡0 ) ) = 0/(1 + 1) = 0/2 = 0 Ex 12.1, 21 (Method 2) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) (𝑙𝑖𝑚)┬(𝑥→0) (cosec x – cot x) = (𝑙𝑖𝑚)┬(𝑥→0) ((𝑐𝑜𝑠𝑒𝑐 𝑥 − 𝑐𝑜𝑡⁡〖𝑥) 〗)/𝟏 = (𝑙𝑖𝑚)┬(𝑥→0) (𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗⁡𝑥)/(𝒄𝒐𝒔𝒆𝒄𝟐 𝒙 − 𝒄𝒐𝒕𝟐 𝒙) = (𝑙𝑖𝑚)┬(𝑥→0) (𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗⁡𝑥)/((𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗⁡〖𝑥) (𝑐𝑜𝑠𝑒𝑐 𝑥 +〖 𝑐𝑜𝑡〗⁡〖𝑥)〗 〗 ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/(𝑐𝑜𝑠𝑒𝑐 𝑥 +〖 𝑐𝑜𝑡〗⁡𝑥 ) (𝑈𝑠𝑖𝑛𝑔 𝑐𝑜𝑠𝑒𝑐2 𝜃−𝑐𝑜𝑡2 𝜃=1) Using cosec θ = (1 )/(sin θ) cot θ = (cos θ)/(sin θ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/(1/𝑠𝑖𝑛⁡𝑥 + 𝑐𝑜𝑠⁡𝑥/𝑠𝑖𝑛⁡𝑥 ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/((1 + 〖 𝑐𝑜𝑠〗⁡𝑥)/𝑠𝑖𝑛⁡𝑥 ) = (𝑙𝑖𝑚)┬(𝑥→0) 𝑠𝑖𝑛⁡𝑥/(1 + 𝑐𝑜𝑠⁡𝑥 ) Putting x = 0 = sin⁡0/(1 +〖 cos〗⁡0 ) = 0/(1 + 1) = 0/2 = 0 Ex 12.1, 21 (Method 3) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) (𝑙𝑖𝑚)┬(𝑥→0) (cosec 𝑥 − cot 𝑥) = (𝑙𝑖𝑚)┬(𝑥→0) 1/sin⁡𝑥 − cos⁡𝑥/sin⁡𝑥 = (𝑙𝑖𝑚)┬(𝑥→0) ((1 − cos⁡𝑥)/sin⁡𝑥 ) Using 1 − cos 2𝜃 = 2 sin2 𝜃 and sin 2𝜃 = 2 sin 𝜃 cos 𝜃 = (𝑙𝑖𝑚)┬(𝑥→0) (2 sin^2⁡〖 𝑥/2〗)/(2 sin⁡〖 𝑥/2〗 cos⁡〖 𝑥/2〗 ) = (𝑙𝑖𝑚)┬(𝑥→0) tan⁡〖𝑥/2〗 Putting x = 0 = tan 0 = 0