Misc 21 - Chapter 5 Class 12 Continuity and Differentiability

Transcript

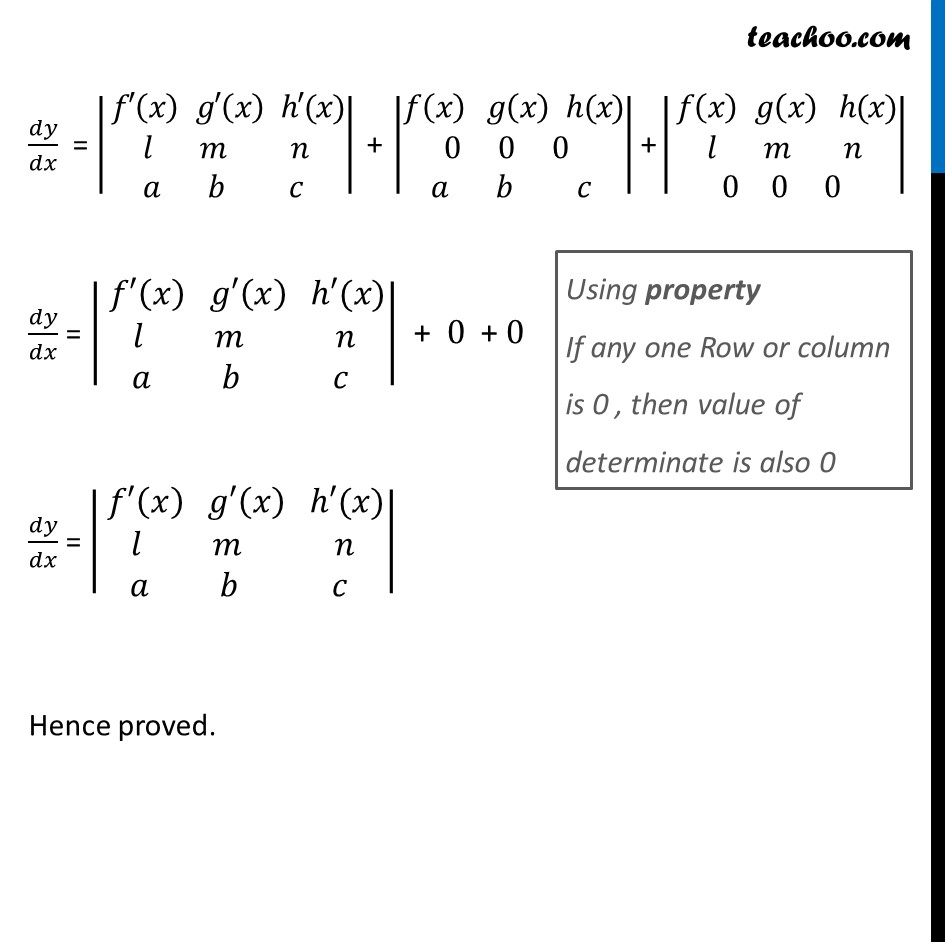
Misc 21 (Method 1) If 𝑦 = |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 Here 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| Expanding determinant 𝑑𝑦/𝑑𝑥 = |𝑓′(𝑥)| |■8(𝑚&𝑛@𝑏&𝑐)||−𝑔′(𝑥) | |■8(𝑙&𝑛@𝑎&𝑐)||1+ ℎ′(𝑥) ||■8(𝑙&𝑚@𝑎&𝑏)| 𝑑𝑦/𝑑𝑥 = 𝑓′(𝑥) (𝑚𝑐 −𝑏𝑛)−𝑔′(𝑛) (𝑙𝑐−𝑎𝑛) + ℎ′(𝑛) (𝑙𝑏−𝑎𝑚) 𝑑𝑦/𝑑𝑥 = (𝑚𝑐 −𝑏𝑛) 𝑓′(𝑥)−(𝑙𝑐−𝑎𝑛)𝑔′(𝑥) +(𝑙𝑏−𝑎𝑚) ℎ′(𝑥) Hence We need to prove that 𝒅𝒚/𝒅𝒙 = (𝑚𝑐 −𝑏𝑛) 𝑓′(𝑥)−(𝑙𝑐−𝑎𝑛)𝑔′(𝑥) +(𝑙𝑏−𝑎𝑚) ℎ′(𝑥) Now, 𝑦 = |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| Expanding determinant 𝑦 = 𝑓(𝑥)|■8(𝑚&𝑛@𝑏&𝑐)|− 𝑔(𝑥)|■8(𝑙&𝑛@𝑎&𝑐)|+ ℎ(𝑥)|■8(𝑙&𝑚@𝑎&𝑏)| 𝑦 = 𝑓(𝑥) (𝑚𝑐 −𝑏𝑛)−𝑔(𝑛) (𝑙𝑐−𝑎𝑛) + ℎ(𝑛) (𝑙𝑏−𝑎𝑚) 𝑦 = (𝑚𝑐 −𝑏𝑛) 𝑓(𝑥)−(𝑙𝑐−𝑎𝑛)𝑔(𝑥)" +" (𝑙𝑏−𝑎𝑚) ℎ(𝑥)" " Differentiating 𝑤.𝑟.𝑡.𝑥. 𝑑𝑦/𝑑𝑥 = 𝑑((𝑚𝑐 − 𝑏𝑛) 𝑓(𝑥) − (𝑙𝑐 − 𝑎𝑛)𝑔(𝑥)" +" (𝑙𝑏 − 𝑎𝑚) ℎ(𝑥)" " )/𝑑𝑥 𝑑𝑦/𝑑𝑥 = 𝑑((𝑚𝑐 − 𝑏𝑛) 𝑓(𝑥))/𝑑𝑥 − 𝑑((𝑙𝑐 − 𝑎𝑛)𝑔(𝑥))/𝑑𝑥 + 𝑑((𝑙𝑏 − 𝑎𝑚) ℎ(𝑥))/𝑑𝑥 𝑑𝑦/𝑑𝑥 = (𝑚𝑐−𝑏𝑛) 𝑑(𝑓(𝑥))/𝑑𝑥 − (𝑙𝑐−𝑎𝑛) 𝑑(𝑔(𝑥))/𝑑𝑥 + (𝑙𝑏−𝑎𝑚) 𝑑(ℎ(𝑥))/𝑑𝑥 𝑑𝑦/𝑑𝑥 = (𝑚𝑐−𝑏𝑛) 𝑓′(𝑥)−(𝑙𝑐−𝑎𝑛) 𝑔′(𝑥) + (𝑙𝑏−𝑎𝑚) ℎ′(𝑥)" " Hence proved Misc 21 (Method 2) If 𝑦 = |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| , prove that 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| To Differentiate a determinant, We differentiate one row (or one column) at a time keeping others unchanged If 𝑦 = |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| + |█(𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@(𝑙)^′ (𝑚)^′ (𝑛)^′@𝑎 𝑏 𝑐 )| + |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@(𝑎)′ (𝑏)′ (𝑐)′ )| 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| + |█(𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@0 0 0 @𝑎 𝑏 𝑐 )| + |█( 𝑓(𝑥) 𝑔(𝑥) ℎ(𝑥)@𝑙 𝑚 𝑛@0 0 0 )| 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| + 0 + 0 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )| Hence proved. Using property If any one Row or column is 0 , then value of determinate is also 0 𝑐 )| , prove that 𝑑𝑦/𝑑𝑥 = |█( 𝑓′(𝑥) 𝑔′(𝑥) ℎ′(𝑥)@𝑙 𝑚 𝑛@𝑎 𝑏 𝑐 )|