Misc 15 - Chapter 5 Class 12 Continuity and Differentiability (Term 1)

Transcript

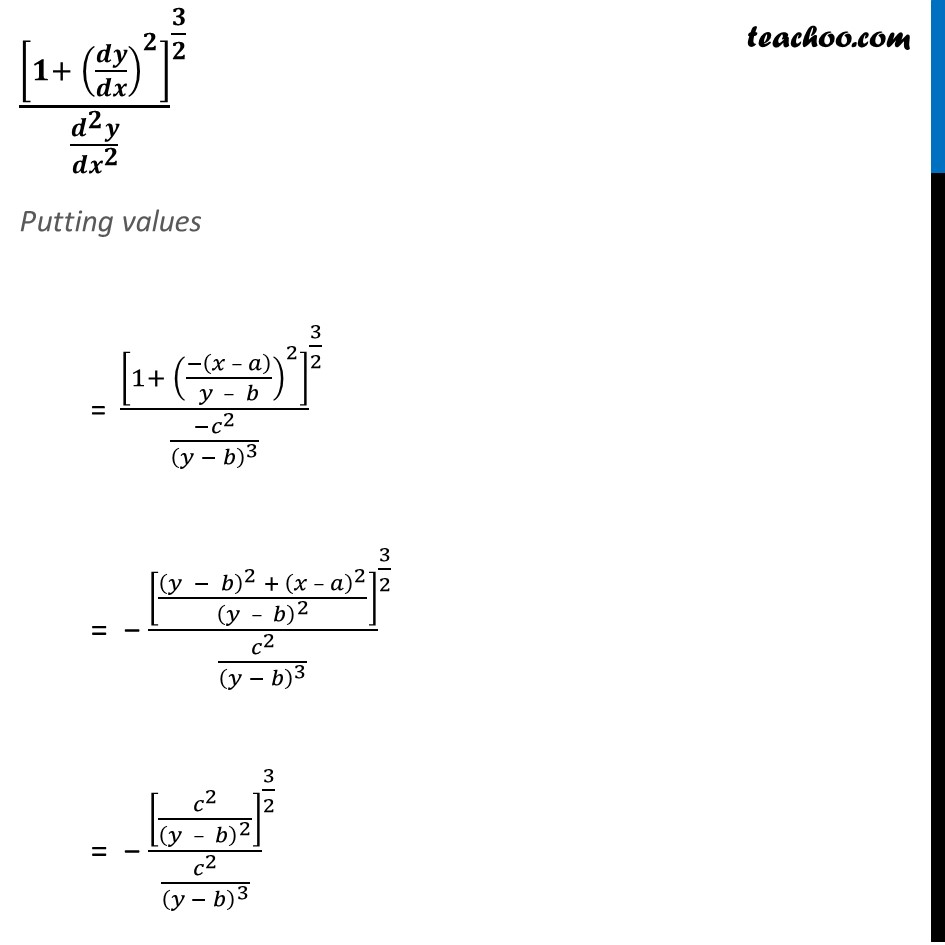
Misc 15 If (𝑥 – 𝑎)^2+ (𝑦 – 𝑏)^2= 𝑐2, for some 𝑐 > 0, prove that 〖[1 + (𝑑𝑦/𝑑𝑥)^2 ]/((𝑑^2 𝑦)/〖𝑑𝑥〗^2 )〗^(3/2)is a constant independent of a and b.First we will calculate 𝑑𝑦/𝑑𝑥 (𝑥 – 𝑎)^2+ (𝑦 – 𝑏)^2= 𝑐2 Differentiating 𝑤.𝑟.𝑡.𝑥. 𝑑((𝑥 – 𝑎)^2+ (𝑦 – 𝑏)^2 )/𝑑𝑥 = 𝑑(𝑐^2 )/𝑑𝑥 𝑑((𝑥 – 𝑎)^2 )/𝑑𝑥 +" " 𝑑((𝑦 – 𝑏)^2 )/𝑑𝑥 = 0 2(𝑥 – 𝑎). 𝑑(𝑥 − 𝑎)/𝑑𝑥 + 2 (𝑦 – 𝑏). 𝑑(𝑦 − 𝑏)/𝑑𝑥 = 0 2 (𝑥 – 𝑎) (1 −0) + 2(𝑦 – 𝑏) . (𝑑𝑦/𝑑𝑥 −0) = 0 2 (𝑥 – 𝑎) + 2(𝑦 – 𝑏) . (𝑑𝑦/𝑑𝑥) = 0 2(𝑦 – 𝑏) . 𝑑𝑦/𝑑𝑥 = −2 (𝑥 – 𝑎) 𝑑𝑦/𝑑𝑥 = (−2 (𝑥 – 𝑎))/2(𝑦 – 𝑏) 𝒅𝒚/𝒅𝒙 = (−(𝒙 − 𝒂))/(𝒚 − 𝒃) Again Differentiating 𝑤.𝑟.𝑡.𝑥. 𝑑/𝑑𝑥 (𝑑𝑦/𝑑𝑥) = 𝑑/𝑑𝑥 ((−(𝑥 − 𝑎))/(𝑦 − 𝑏)) (𝑑^2 𝑦)/(𝑑𝑥^2 ) = − 𝑑/𝑑𝑥 ((𝑥 − 𝑎)/(𝑦 − 𝑏)) (𝑑^2 𝑦)/(𝑑𝑥^2 )= − ((𝑑(𝑥 – 𝑎)/𝑑𝑥 (𝑦 – 𝑏) − 𝑑(𝑦 – 𝑏)/𝑑𝑥 . (𝑥 – 𝑎))/(𝑦 − 𝑏)^2 ) (𝑑^2 𝑦)/(𝑑𝑥^2 ) = − (((1 − 0) (𝑦 – 𝑏) − (𝑑𝑦/𝑑𝑥 − 0)(𝑥 – 𝑎))/(𝑦 − 𝑏)^2 ) Using Quotient rule As (𝑢/𝑣)′ = (𝑢^′ 𝑣 − 𝑣^′ 𝑢)/𝑣^2 where u = x − 𝑎 & v = y − b (𝑑^2 𝑦)/(𝑑𝑥^2 ) = − (((𝑦 – 𝑏) − (𝑑𝑦/𝑑𝑥)(𝑥 – 𝑎))/(𝑦 − 𝑏)^2 ) (𝑑^2 𝑦)/(𝑑𝑥^2 ) = − (((𝑦 – 𝑏) − (− (𝑥 – 𝑎))/((𝑦 – 𝑏) ) (𝑥 – 𝑎))/(𝑦 − 𝑏)^2 ) (𝑑^2 𝑦)/(𝑑𝑥^2 )= − (((𝑦 – 𝑏)^2 + (𝑥 – 𝑎)^2)/((𝑦 − 𝑏)^2 (𝑦 − 𝑏) )) (𝒅^𝟐 𝒚)/(𝒅𝒙^𝟐 )= (−𝒄^𝟐)/(𝒚 − 𝒃)^𝟑 Now, finding value of 〖[𝟏+ (𝒅𝒚/𝒅𝒙)^𝟐 ]/((𝒅^𝟐 𝒚)/〖𝒅𝒙〗^𝟐 )〗^(𝟑/𝟐) (Given (𝑥 – 𝑎)^2+ (𝑦 – 𝑏)^2= 𝑐2) 〖[𝟏+ (𝒅𝒚/𝒅𝒙)^𝟐 ]/((𝒅^𝟐 𝒚)/〖𝒅𝒙〗^𝟐 )〗^(𝟑/𝟐) Putting values = 〖[1+ ((−(𝑥 – 𝑎))/(𝑦 – 𝑏))^2 ]/((−𝑐^2)/(𝑦 − 𝑏)^3 )〗^(3/2) = − 〖[((𝑦 − 𝑏)^2 + (𝑥 – 𝑎)^2)/(𝑦 – 𝑏)^2 ]/(𝑐^2/(𝑦 − 𝑏)^3 )〗^(3/2) = − 〖[𝑐^2/(𝑦 – 𝑏)^2 ]/(𝑐^2/(𝑦 − 𝑏)^3 )〗^(3/2) = − [𝑐^2/(𝑦 – 𝑏)^2 ]^(3/2) × (𝑦 − 𝑏)^3/𝑐^2 = − (𝑐/(𝑦 – 𝑏))^(2 × 3/2) × (𝑦 − 𝑏)^3/𝑐^2 "= −" (𝑐/(𝑦 – 𝑏))^3 " × " (𝑦 − 𝑏)^3/𝑐^2 "= −" 𝑐^3/𝑐^2 × (𝑦 − 𝑏)^3/(𝑦 − 𝑏)^3 = −𝒄 = Constant Which is constant independent of a & b Hence proved