Example 37 - Chapter 13 Class 12 Probability (Term 2)
Last updated at Feb. 15, 2020 by Teachoo
Examples
Example 1
Example 2
Example 3
Example 4
Example 5 Important
Example 6
Example 7 Important
Example 8
Example 9 Important
Example 10
Example 11 Important
Example 12 Important
Example 13 Important
Example 14 Important
Example 15 Important
Example 16
Example 17 Important
Example 18 Important
Example 19 Important
Example 20 Important
Example 21 Important
Example 22
Example 23
Example 24 Important
Example 25 Important
Example 26 Important
Example 27 Deleted for CBSE Board 2022 Exams
Example 28 Important Deleted for CBSE Board 2022 Exams
Example 29 Important Deleted for CBSE Board 2022 Exams
Example 30 Important Deleted for CBSE Board 2022 Exams
Example 31 Important Deleted for CBSE Board 2022 Exams
Example 32 Important Deleted for CBSE Board 2022 Exams
Example 33 Important
Example 34 Deleted for CBSE Board 2022 Exams
Example 35 Deleted for CBSE Board 2022 Exams
Example 36 Important
Example 37 Important You are here
Chapter 13 Class 12 Probability (Term 2)
Serial order wise
Transcript
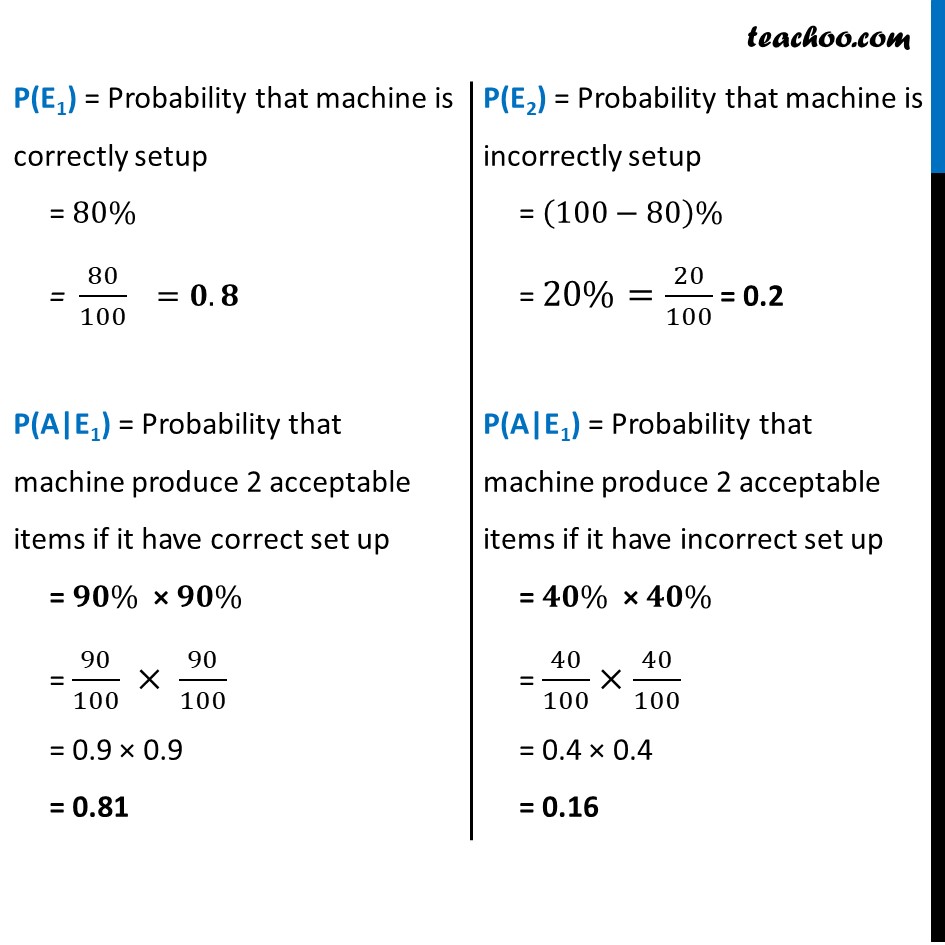
Example 37 If a machine is correctly set up, it produces 90% acceptable items. If it is incorrectly set up, it produces only 40% acceptable items. Past experience shows that 80% of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.Let E1 : Event that the machine is correctly setup E2 : Event that the machine is incorrectly setup A : Event that the Machine produce two acceptable items We need to find out the probability that the machine have a correct set up if it produce two acceptable item i.e. P(E1|A) P(E1|A) = (π(πΈ_1 ).π(π΄|πΈ_1))/(π(πΈ_1 ).π(π΄|πΈ_1)+π(πΈ_2 ).π(π΄|πΈ_2) ) "P(E1)" = Probability that machine is correctly setup = 80% = 80/100 =0.8 P(A|E1) = Probability that machine produce 2 acceptable items if it have correct set up = ππ% Γ ππ% = 90/100 Γ 90/100 = 0.9 Γ 0.9 = 0.81 "P(E2)" = Probability that machine is incorrectly setup = (100β80)% = 20%=20/100 = 0.2 P(A|E1) = Probability that machine produce 2 acceptable items if it have incorrect set up = ππ% Γ ππ% = 40/100Γ40/100 = 0.4 Γ 0.4 = 0.16 Putting values in the formula P(E1|A) = (π(πΈ_1 ).π(π΄|πΈ_1))/(π(πΈ_1 ).π(π΄|πΈ_1)+π(πΈ_2 ).π(π΄|πΈ_2) ) = (0.8 Γ π.ππ)/(0.8 Γ π.ππ + 0.2 Γ π.ππ) = 0.648/0.680 = 0.95
