Example 28 - Chapter 3 Class 11 Trigonometric Functions

Transcript

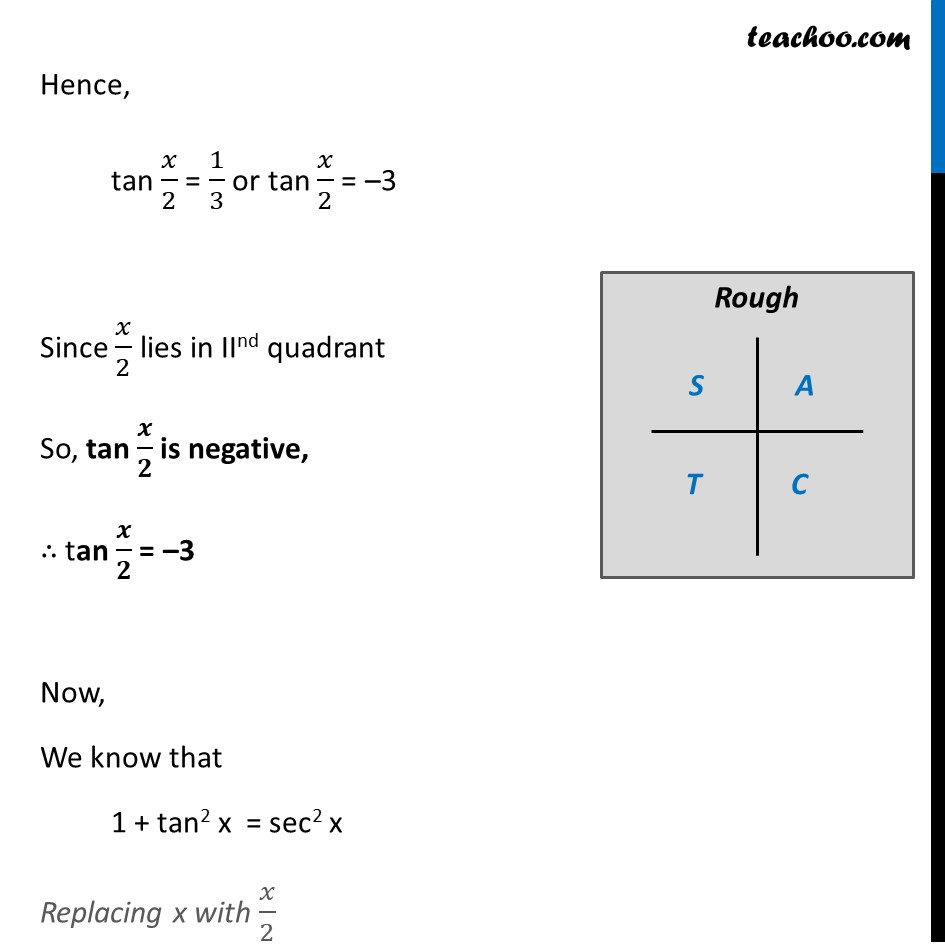
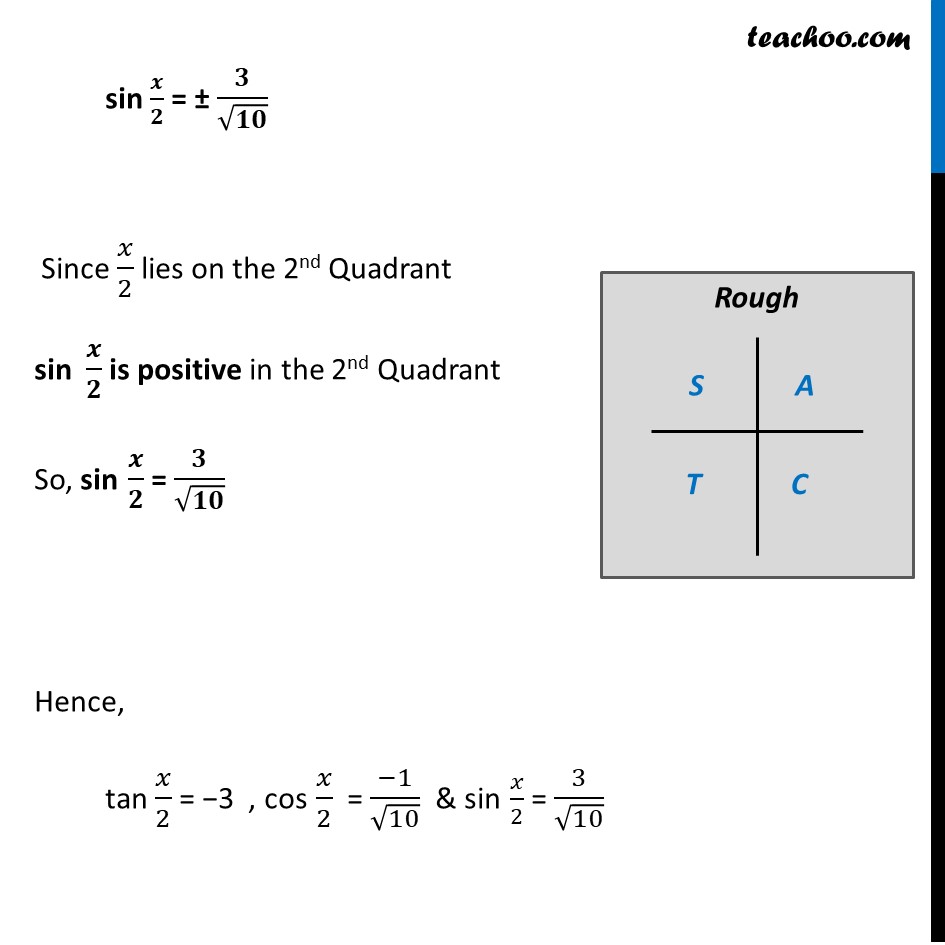
Example 28 If tan⁡𝑥 = 3/4 , "π" < 𝑥 < 3𝜋/4 , find the value of sin 𝑥/2 , cos 𝑥/2 and tan 𝑥/2 Given that "π" < x < 3𝜋/2 i.e.180° < x < 3/2 × 180° i.e. 180° < x < 270° Dividing by 2 all sides (180°)/2 < 𝑥/2 < (270°)/2 90° < 𝑥/2 < 135° So, 𝑥/2 lies in 2nd quadrant In 2nd quadrant, sin is positive, cos & tan are negative sin 𝑥/2 is positive, cos 𝑥/2 and tan 𝑥/2 are negative Given tan x = 3/4 We know that tan 2x = (2 𝑡𝑎𝑛⁡𝑥)/(1 − 𝑡𝑎𝑛2𝑥) Replacing x with 𝑥/2 tan (2𝑥/2) = (2 𝑡𝑎𝑛⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) tan x = (2 𝑡𝑎𝑛⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) tan x = (2 tan⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) 3/4 = (2 tan⁡(𝑥/2))/(1 − 𝑡𝑎𝑛2(𝑥/2) ) 3(1 – tan2 (𝑥/2) = 4 × 2 tan (𝑥/2) 3 × 1 – 3 × tan2 (𝑥/2) = 8 tan (𝑥/2) 3 × 1 – 3 × tan2 (𝑥/2) = 8 tan (𝑥/2) 3 – 3 tan2 (𝑥/2) = 8 tan (𝑥/2) 0 = –3 + 3tan2 (𝑥/2) + 8 tan 𝑥/2 Replacing tan 𝐱/𝟐 by a Our equation becomes 0 = –3 + 3a2 + 8a 3a2 + 8a – 3 = 0 3a2 + 9a – a – 3 = 0 3a (a + 3) – 1 (a + 3) = 0 (3a – 1) (a + 3) = 0 Hence So, a = 1/3 or a = –3 3a – 1 = 0 3a = 1 a = 1/3 a + 3 = 0 a = −3 Hence, tan 𝑥/2 = 1/3 or tan 𝑥/2 = –3 Since 𝑥/2 lies in IInd quadrant So, tan 𝑥/2 is negative, ∴ tan 𝒙/𝟐 = –3 Now, We know that 1 + tan2 x = sec2 x Replacing x with 𝑥/2 1 + tan2 𝑥/2 = sec2 𝑥/2 1 + (–3)2 = sec2 𝑥/2 1 + 9 = sec2 x/2 1 + 9 = sec2 x/2 10 = sec2 𝑥/2 sec2 𝑥/2 = 10 sec 𝑥/2 = ± √10 Since 𝑥/2 lie on the llnd Quadrant, cos 𝑥/2 is negative in the llnd Quadrant ∴ sec 𝑥/2 is negative in the llnd Quadrant So, sec 𝒙/𝟐 = −√𝟏𝟎 Therefore, cos 𝒙/𝟐 = (−𝟏)/√𝟏𝟎 Now, We know that sin2x + cos2x = 1 Replacing x with 𝑥/2 sin2 𝑥/2 + cos2 𝑥/2 = 1 sin2 𝑥/2 = 1 – cos2 𝑥/2 Putting cos 𝑥/2 = −1/√10 sin2 𝑥/2 = 1 – ((−1)/√10)2 sin2 𝑥/2 = 1 – 1/10 sin2 𝑥/2 = (10 − 1)/10 sin2 𝑥/2 = 9/10 sin 𝑥/2 = ± √(9/10) sin 𝑥/2= ± √9/√10 sin 𝑥/2 = ± 3/√10 Since 𝑥/2 lies on the 2nd Quadrant sin 𝑥/2 is positive in the 2nd Quadrant So, sin 𝒙/𝟐 = 𝟑/√𝟏𝟎 Hence, tan 𝑥/2 = −3 , cos 𝑥/2 = (−1)/√10 & sin 𝑥/2 = 3/√10