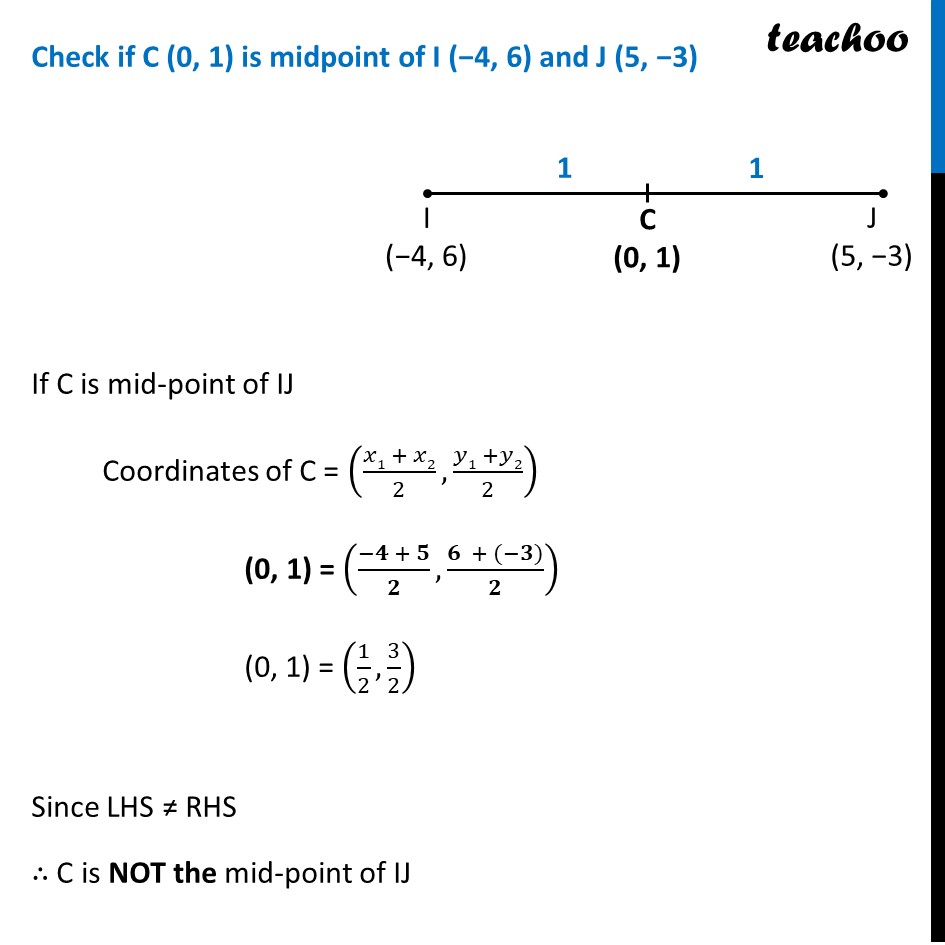
Check if the Full-back J(5,-3) and centre-back I(-4,6) are equidistant

Check if the Full-back J(5,-3) and centre-back I(-4,6) are equidistant from forward C(0,1) and if C is the mid-point of IJ.

We need to check if C is equidistant from J and I And C is mid-point of IJ Doing this one by one Check if C (0, 1) is equidistant from I (−4, 6) and J (5, −3) To prove if point C is equidistant from I & J We need to prove CI = CJ Since CI = CJ ∴ C is equidistant from I and J Finding CI CI = √(( −𝟒 −𝟎)𝟐+(𝟔−𝟏)𝟐) = √((−4)2+(5)2) = √(16+25 ) = √𝟒𝟏 Finding CJ CJ = √(( 𝟓 −𝟎)𝟐+(−𝟑−𝟏)𝟐) = √((5)2+(−4)2) = √(25+16 ) = √𝟒𝟏 Check if C (0, 1) is midpoint of I (−4, 6) and J (5, −3) If C is mid-point of IJ Coordinates of C = ((𝑥1 + 𝑥2)/2,(𝑦1 +𝑦2)/2) (0, 1) = ((−𝟒 + 𝟓)/𝟐,(𝟔 + (−𝟑))/𝟐) (0, 1) = (1/2,3/2) Since LHS ≠ RHS ∴ C is NOT the mid-point of IJ Now, AC = BC √(𝒂𝟐−𝟒𝒂+𝟖) = √(𝒂𝟐−𝟏𝟒𝒂+𝟔𝟓) Squaring both sides (√(𝑎2−4𝑎+8) " )2 = (" √(𝑎2−14𝑎+65))^2 𝒂𝟐−𝟒𝒂+𝟖 = 𝒂𝟐−𝟏𝟒𝒂+𝟔𝟓 −4a + 8 = −14a + 65 −4a + 14a = 65 − 8 10a = 57 a = 57/10 a = 5.7

Question 37 (ii) (Choice 2) - CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards