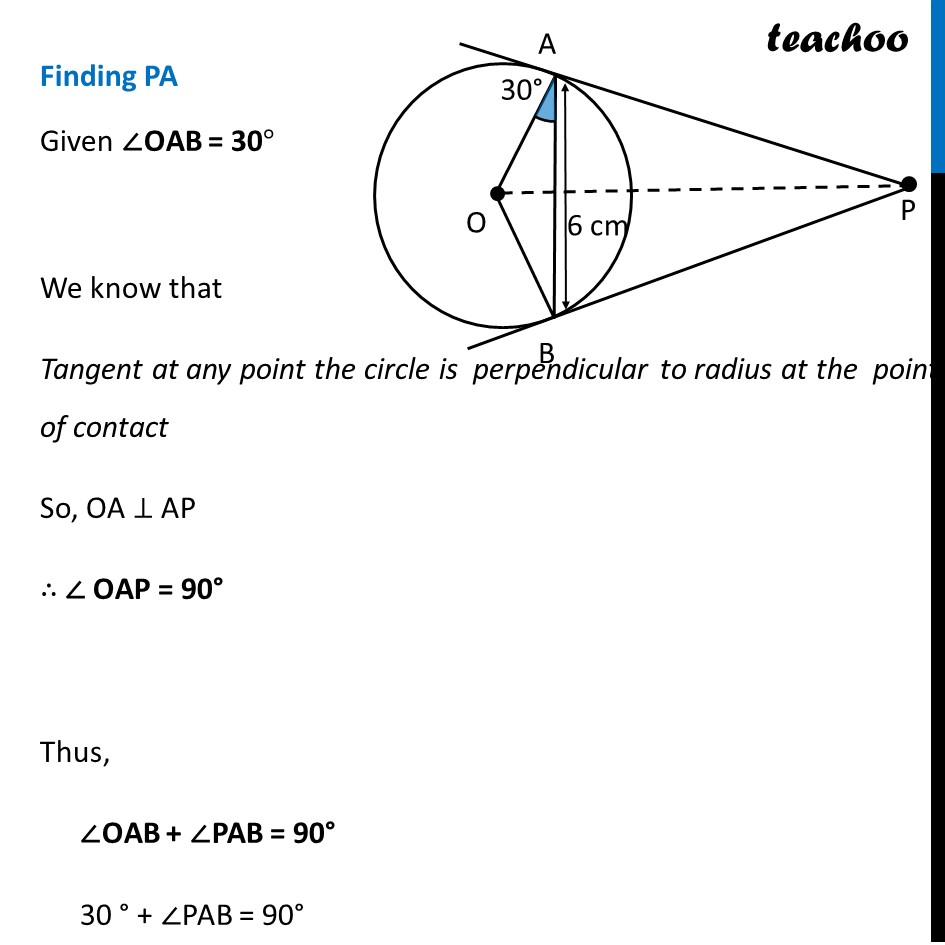
PA and PB are tangents drawn to a circle of centre O from an external

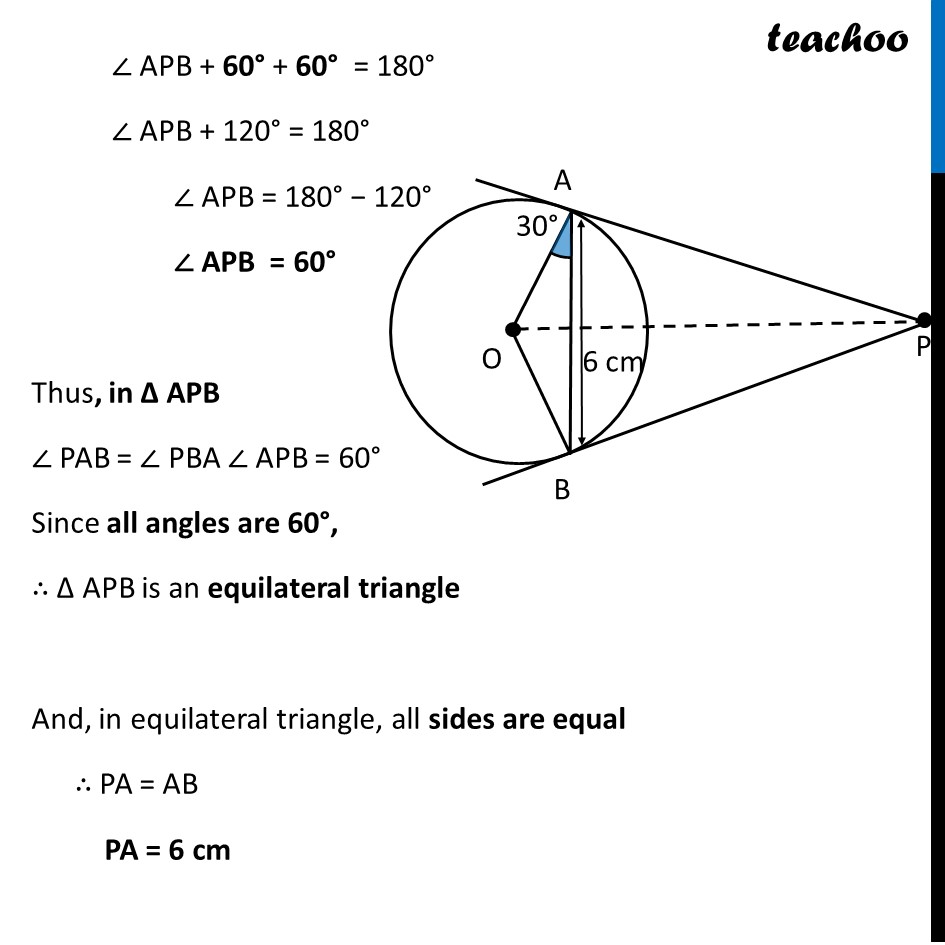
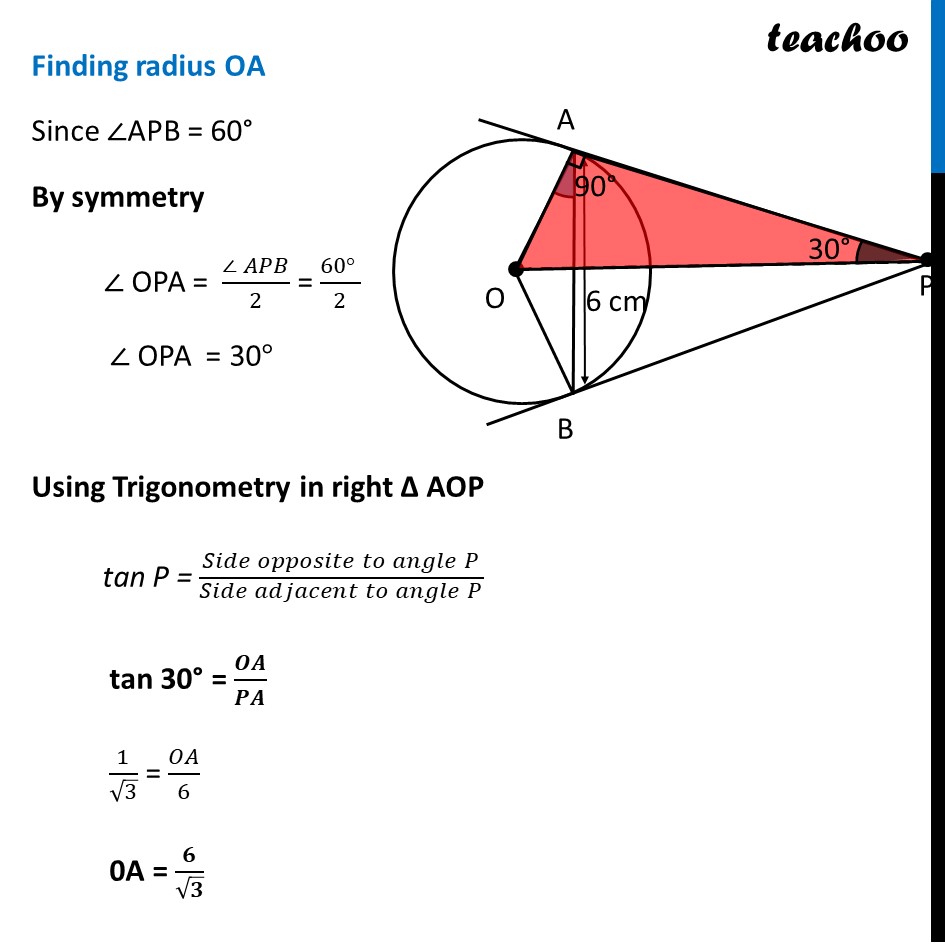
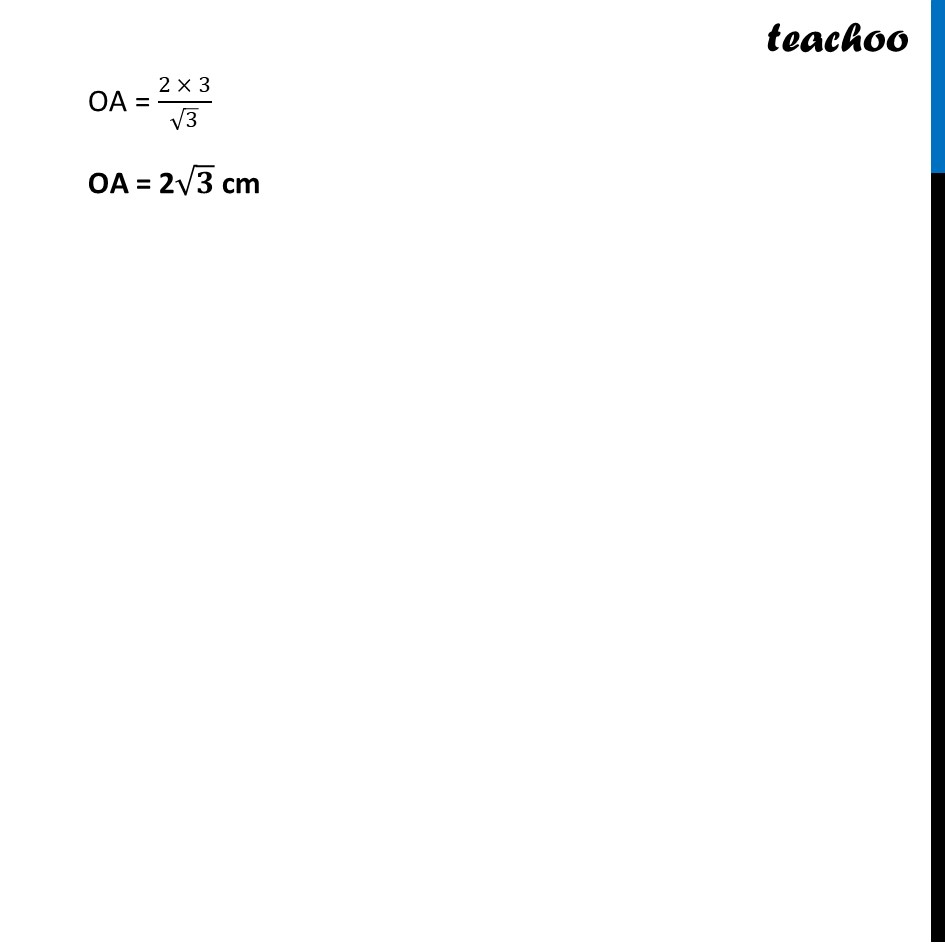
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA ∠PAB = 90° − 30 ° ∴ ∠PAB = 60° Also, since Tangents from external point are equal PA = PB And we know angles opposite to equal sides are equal Thus, ∠ PAB = ∠ PBA = 60° In Δ APB By Angle Sum property ∠ APB + ∠ PAB + ∠ PBA = 180° ∠ APB + 60° + 60° = 180° ∠ APB + 120° = 180° ∠ APB = 180° − 120° ∠ APB = 60° Thus, in Δ APB ∠ PAB = ∠ PBA ∠ APB = 60° Since all angles are 60°, ∴ Δ APB is an equilateral triangle And, in equilateral triangle, all sides are equal ∴ PA = AB PA = 6 cm Finding radius OA Since ∠APB = 60° By symmetry ∠ OPA = (∠ 𝐴𝑃𝐵)/2 = (60° )/2 ∠ OPA = 30° Using Trigonometry in right Δ AOP tan P = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃)/█(𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒" " 𝑃@ ) tan 30° = 𝑶𝑨/𝑷𝑨 1/√3 = 𝑂𝐴/6 0A = 𝟔/√𝟑 OA = (2 × 3)/√3 OA = 2√𝟑 cm

Question 29 (Choice 1) - CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA

Transcript

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular