Question 25 (Choice 1) - CBSE Class 10 Sample Paper for 2024 Boards - Maths Standard - Solutions of Sample Papers for Class 10 Boards

Last updated at Dec. 13, 2024 by Teachoo

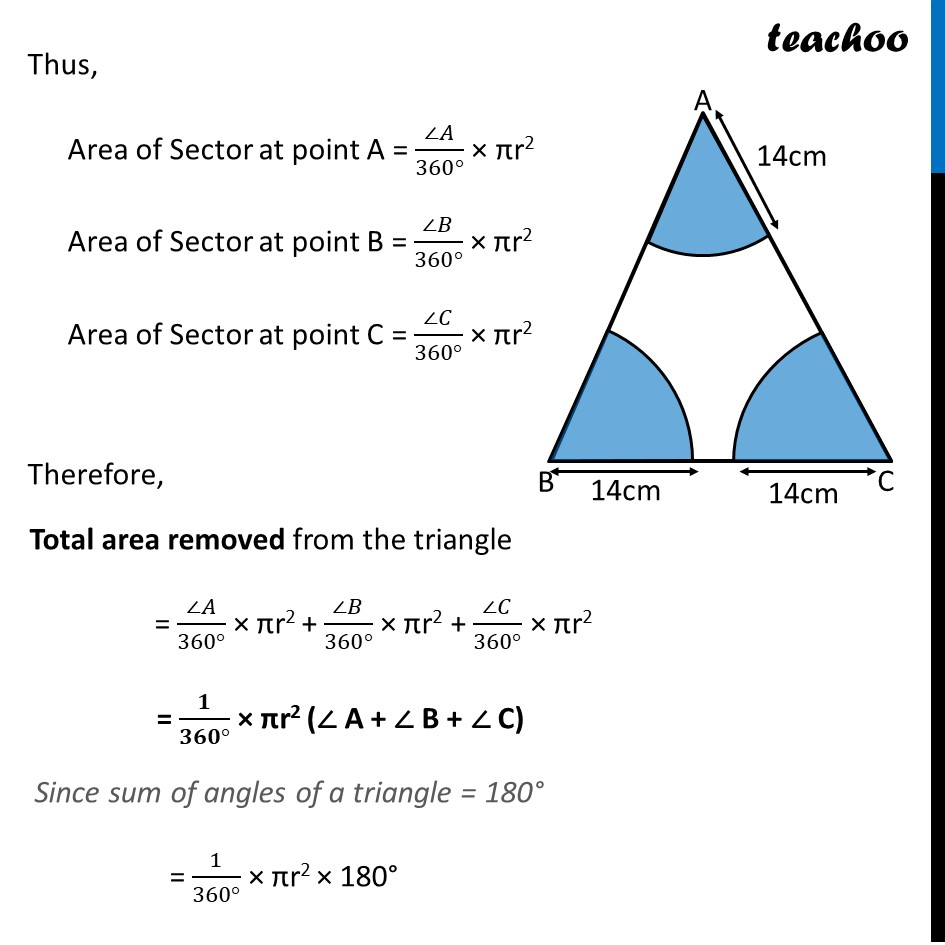
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.

Next: Question 25 (Choice 2) → Go Ad-free

Transcript

Total area removed from the triangle = Area of sector at point A + Area of sector at point B + Area of sector at point C Area of Sector We know that Area of sector = 𝜃/(360°) × πr2 and radius = 14 cm Thus, Area of Sector at point A = (∠𝐴)/(360°) × πr2 Area of Sector at point B = (∠𝐵)/(360°) × πr2 Area of Sector at point C = (∠𝐶)/(360°) × πr2 Therefore, Total area removed from the triangle = (∠𝐴)/(360°) × πr2 + (∠𝐵)/(360°) × πr2 + (∠𝐶)/(360°) × πr2 = 𝟏/(𝟑𝟔𝟎°) × πr2 (∠ A + ∠ B + ∠ C) Since sum of angles of a triangle = 180° = 1/(360°) × πr2 × 180° = 𝟏/𝟐 × πr2 Putting r = 14cm = 1/2 × 22/7 × (14)2 = 11/7 × 14 × 14 = 11 × 28 = 308 〖𝒄𝒎〗^𝟐

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular