Question 3 - Miscellaneous - Chapter 9 Class 12 Differential Equations

Transcript

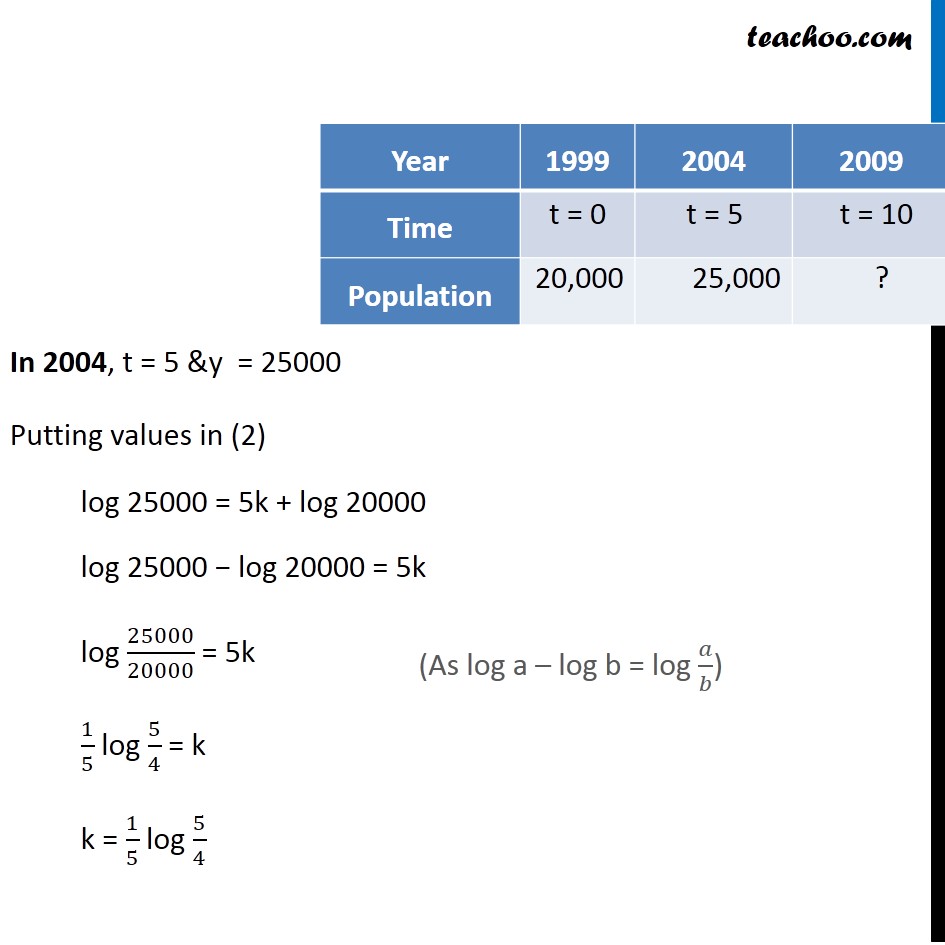
Question 3 The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20,000 in 1999 and 25000 in the year 2004 , what will be the population of the village in 2009 ? Let the population at time t be y Given that population increases continuously at rate proportional to the number of its inhabitants present at any time 𝑑𝑦/𝑑𝑡 ∝ y 𝑑𝑦/𝑑𝑡 = ky 𝑑𝑦/𝑦 = k dt Integrating both sides ∫1▒𝑑𝑦/𝑦=𝑘∫1▒𝑑𝑡 log y = kt + C In 1999, t = 0 & y = 20000 log 20000 = k(0) + C C = log 20000 Put value in (1) log y = kt + C log y = kt + log 20000 In 2004, t = 5 &y = 25000 Putting values in (2) In 2004, t = 5 &y = 25000 Putting values in (2) log 25000 = 5k + log 20000 log 25000 − log 20000 = 5k log 25000/20000 = 5k 1/5 log 5/4 = k k = 1/5 log 5/4 (As log a – log b = log 𝑎/𝑏) Putting value of k in (2) log y = kt + log 20000 log y = 𝑡/5 log 5/4 + log 20000 Now, In 2009, t = 10 , we need to find value of y Putting t = 10 in (3) log 𝑦 = 10/5 log 5/4 + log 20000 log y − log 20000 = 2 log 5/4 log 𝑦/20000 = log (5^2/4^2 ) log 𝑦/20000 = log 25/16 …(3) Removing log 𝑦/20000 = 25/16 y = 25/16×20000 y = 31250 ∴ Population of village in 2009 is 31250