Question 6 - Area of Triangles - Areas of Parallelograms and Triangles

Transcript

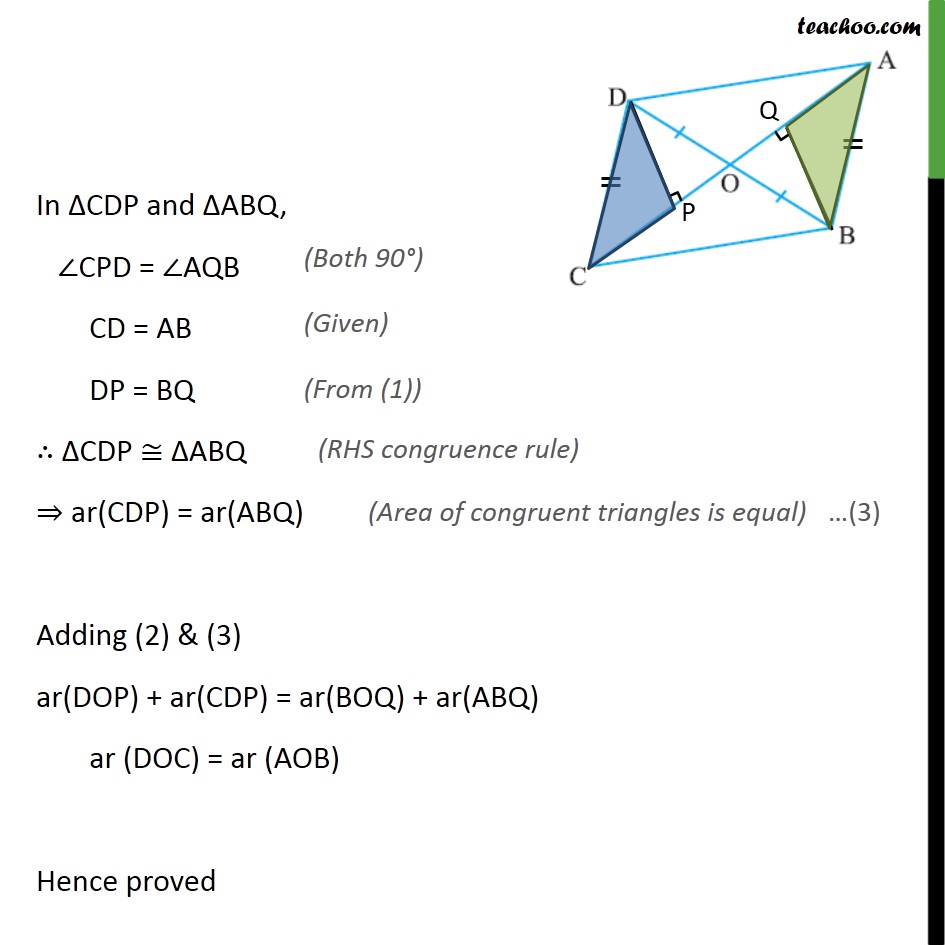
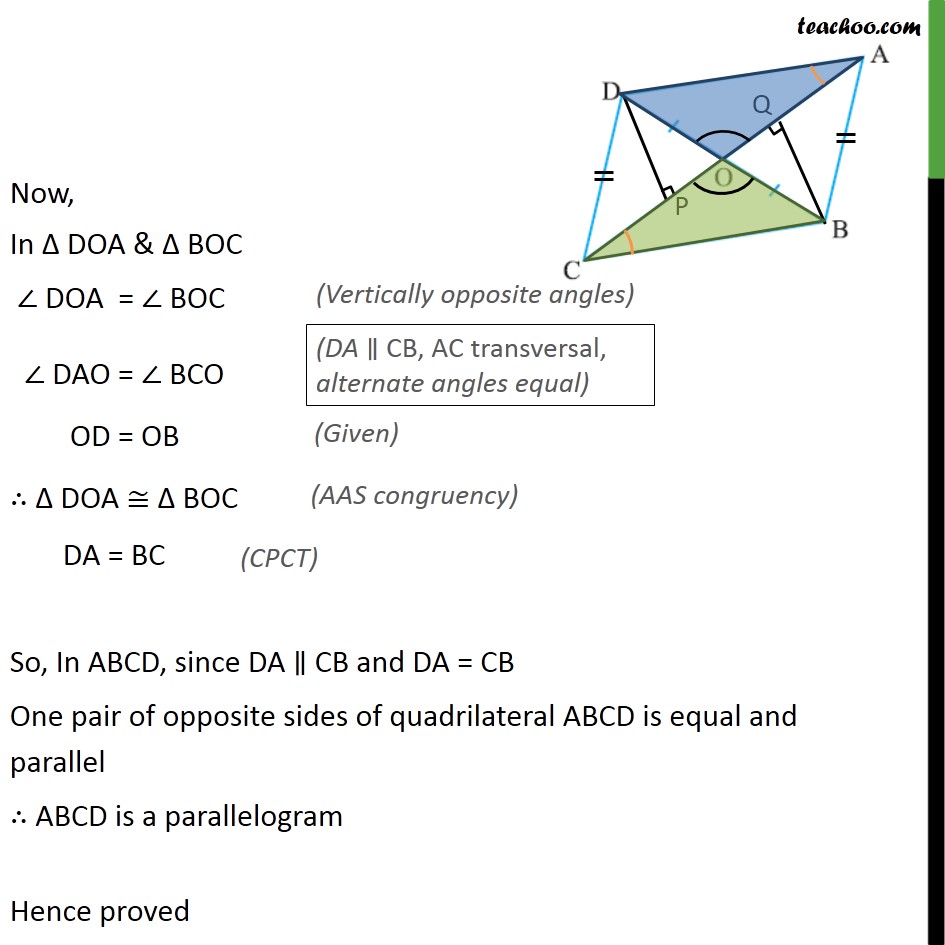
Ex9.3, 6 In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that: (i) ar (DOC) = ar (AOB) Given: A quadrilateral ABCD where OB = OD & AB = CD To prove: ar (DOC) = ar (AOB) Proof : Let us draw DP AC and BQ AC. In DOP and BOQ, DPO = BQO DOP = BOQ OD = OB DOP BOQ DP = BQ & ar(DOP) = ar(BOQ) In CDP and ABQ, CPD = AQB CD = AB DP = BQ CDP ABQ ar(CDP) = ar(ABQ) Adding (2) & (3) ar(DOP) + ar(CDP) = ar(BOQ) + ar(ABQ) ar (DOC) = ar (AOB) Hence proved Ex9.3, 6 In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that: (ii) ar (DCB) = ar (ACB) In part(i) we proved that ar(DOC) = ar(AOB) Adding ar(OCB) both sides, ar(DOC) + ar(OCB) = ar(AOB) + ar(OCB) ar(DCB) = ar(ACB) Question 6 In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that: (iii) DA CB or ABCD is a parallelogram. In the part(ii) we proved ar( DBC) = ar( ABC) We know that two triangles having same base & equal areas, lie between same parallels, Here DBC & ABC are on the same base BC & are equal in area, So, these triangles lie between the same parallels DA and CB DA CB Now, In DOA & BOC DOA = BOC DAO = BCO OD = OB DOA BOC DA = BC So, In ABCD, since DA CB and DA = CB One pair of opposite sides of quadrilateral ABCD is equal and parallel ABCD is a parallelogram Hence proved