Ex 9.3, 5

Transcript

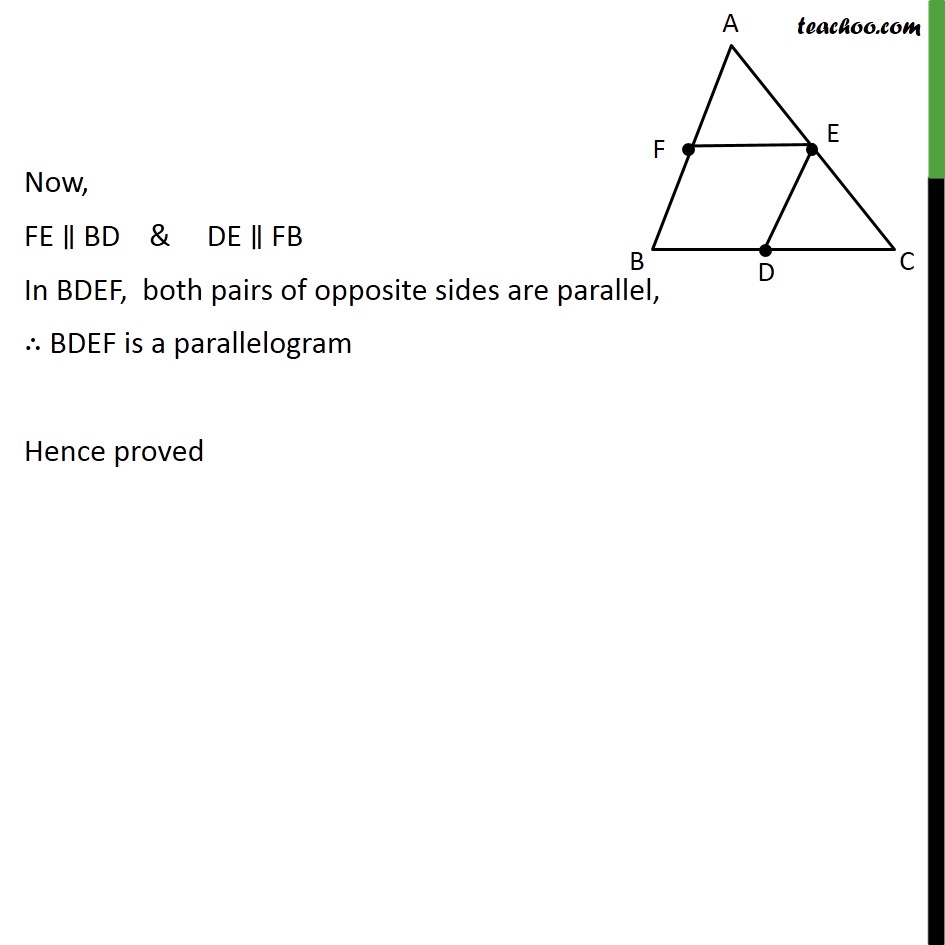
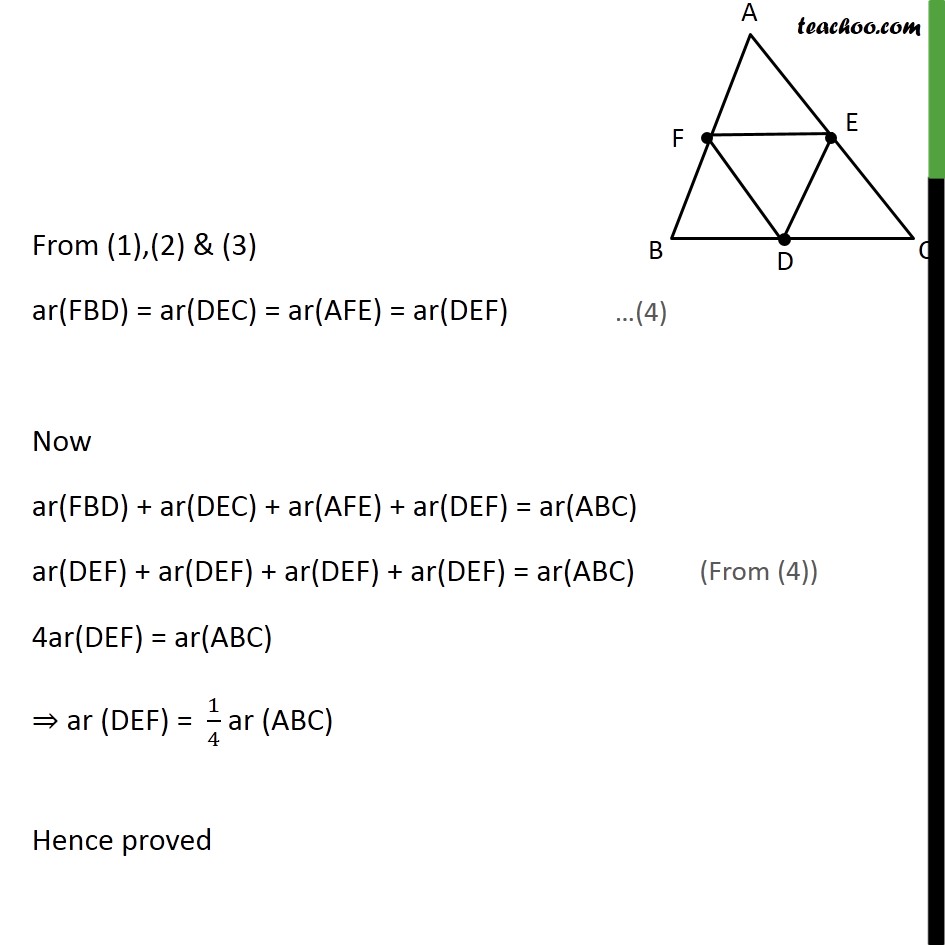
Ex 9.3, 5 D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that (i) BDEF is a parallelogram. Given: ∆ ABC where D, E, F are mid-points of BC, AC & AB respectively To prove: BDEF is a parallelogram Proof : In Δ ABC, F is mid-point of AB, E is mid-point of AC ∴ FE ∥ BC ⇒ FE ∥ BD Now, FE ∥ BD & DE ∥ FB In BDEF, both pairs of opposite sides are parallel, ∴ BDEF is a parallelogram Hence proved Ex 9.3, 5 D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that (ii) ar (DEF) =  1/4 ar (ABC) In part(i) we proved that BDEF is a parallelogram ∴ ∆DBF ≅ ∆ DEF ⇒ ar(DBF) = ar(DEF) Similarly, we can prove FDCE is a parallelogram ∴ ∆DEC ≅ ∆ DEF ⇒ ar(DEC) = ar(DEF) Similarly, we can prove AFDE is a parallelogram ∴ ∆AFE ≅ ∆ DEF ⇒ ar(AFE) = ar(DEF) From (1),(2) & (3) ar(FBD) = ar(DEC) = ar(AFE) = ar(DEF) Now ar(FBD) + ar(DEC) + ar(AFE) + ar(DEF) = ar(ABC) ar(DEF) + ar(DEF) + ar(DEF) + ar(DEF) = ar(ABC) 4ar(DEF) = ar(ABC) ⇒ ar (DEF) =  1/4 ar (ABC) Hence proved Ex 9.3, 5 D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that (iii) ar (BDEF) = 1/2 ar (ABC) We proved in part(ii) that ar(DEF) = 1/4 ar(ABC) Multiplying both sides by 2 2 × ar(DEF) = 2 × 1/4 ar(ABC) 2 ar(DEF) = 1/2 ar(ABC) ar(DEF) + ar(DEF) = 1/2 ar(ABC) ar(DEF) + ar(FBD) = 1/2 ar(ABC) ar(BDEF) = 1/2 ar(ABC) Hence proved