Question 1 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

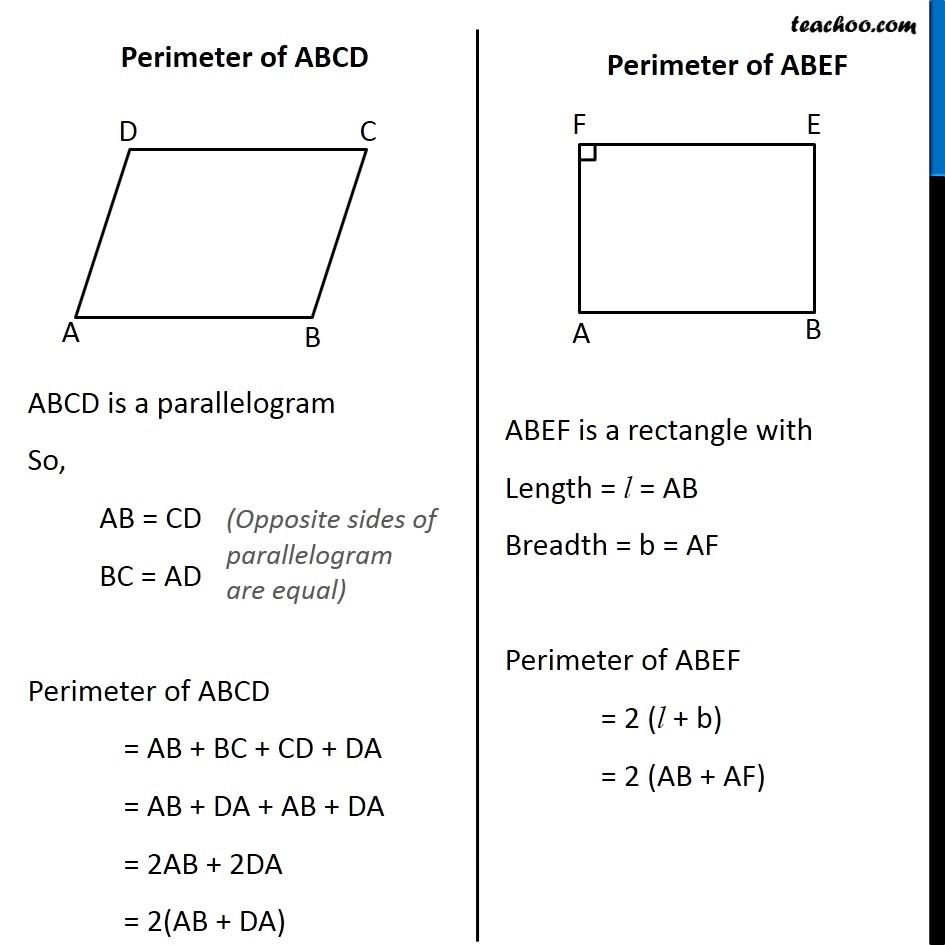
Question 1 Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. Our figure would look like Finding perimeter of ABCD and ABEF Perimeter of ABCD ABCD is a parallelogram So, AB = CD BC = AD (Opposite sides of parallelogram are equal) Perimeter of ABCD = AB + BC + CD + DA = AB + DA + AB + DA = 2AB + 2DA = 2(AB + DA) Perimeter of ABEF ABEF is a rectangle with Length = l = AB Breadth = b = AF Perimeter of ABEF = 2 (l + b) = 2 (AB + AF) Now, As AB is common in both perimeters, we have to prove that DA > AF Now, in right triangle ∆ADF Hypotenuse is the largest side in a right angled triangle. ∴ AD > AF Hence, 2(AB + DA) > 2 (AB + AF) Perimeter of ABCD > Perimeter of ABER ∴ Perimeter of Parallelogram is greater than Perimeter of rectangle.