Question 7 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

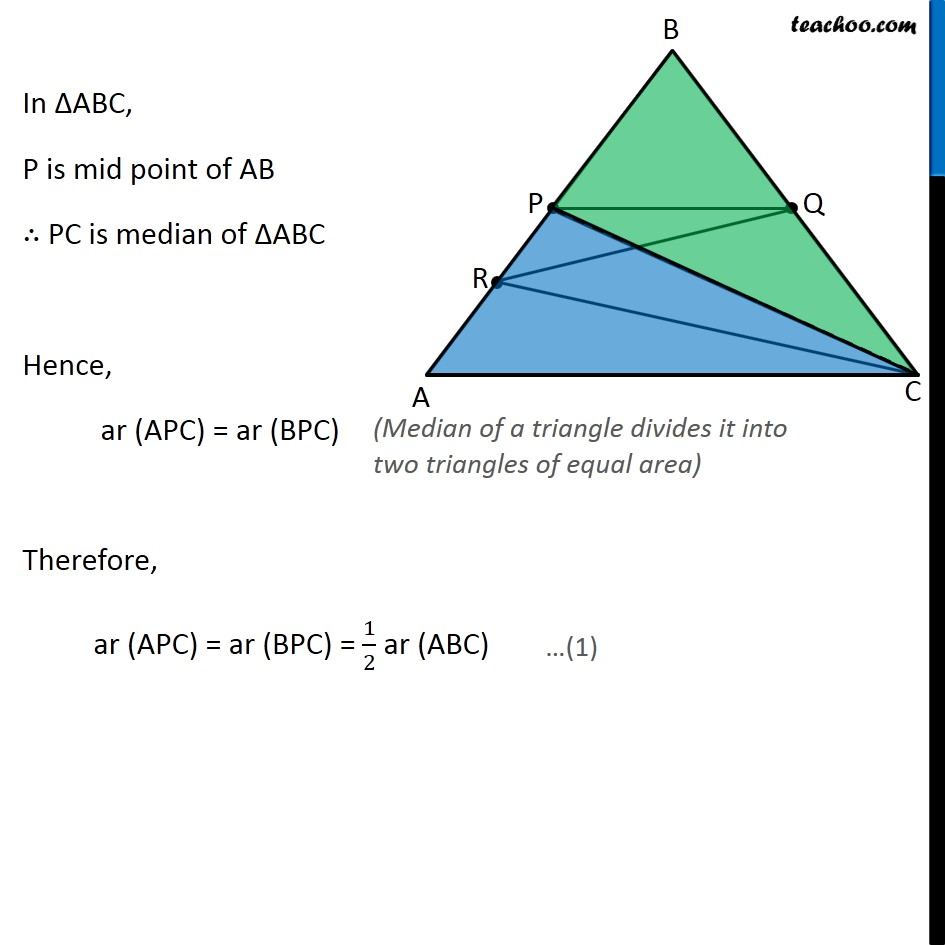
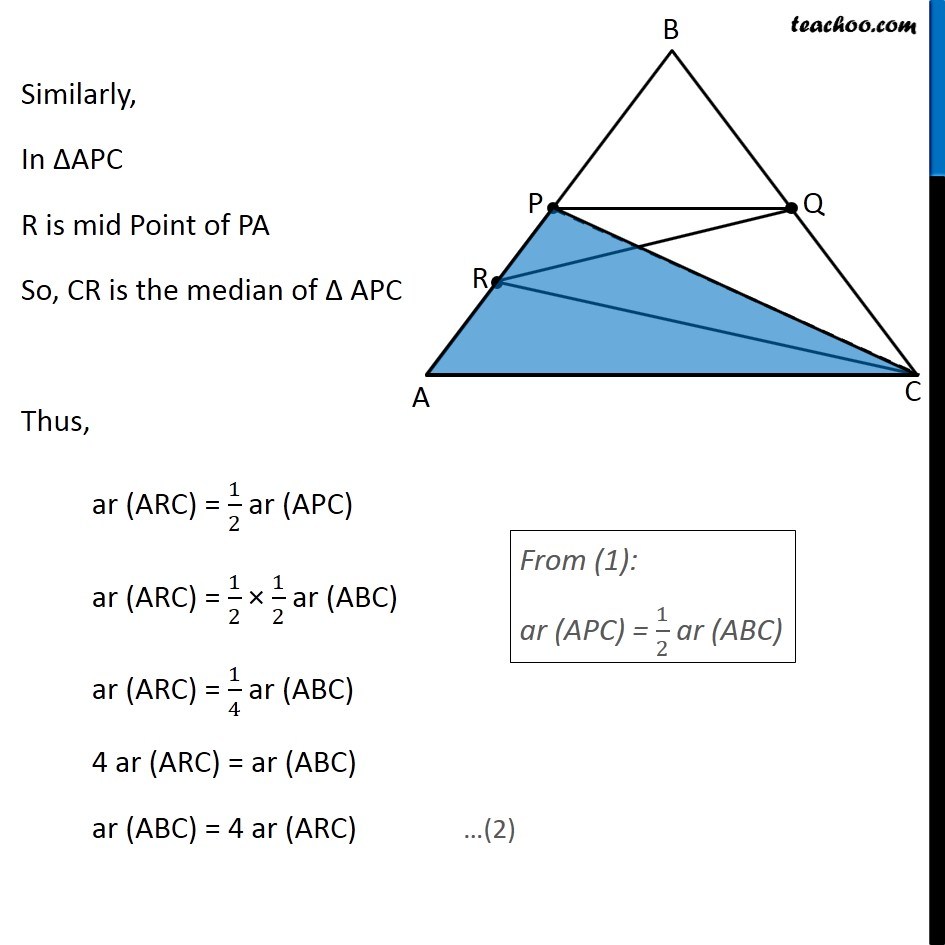
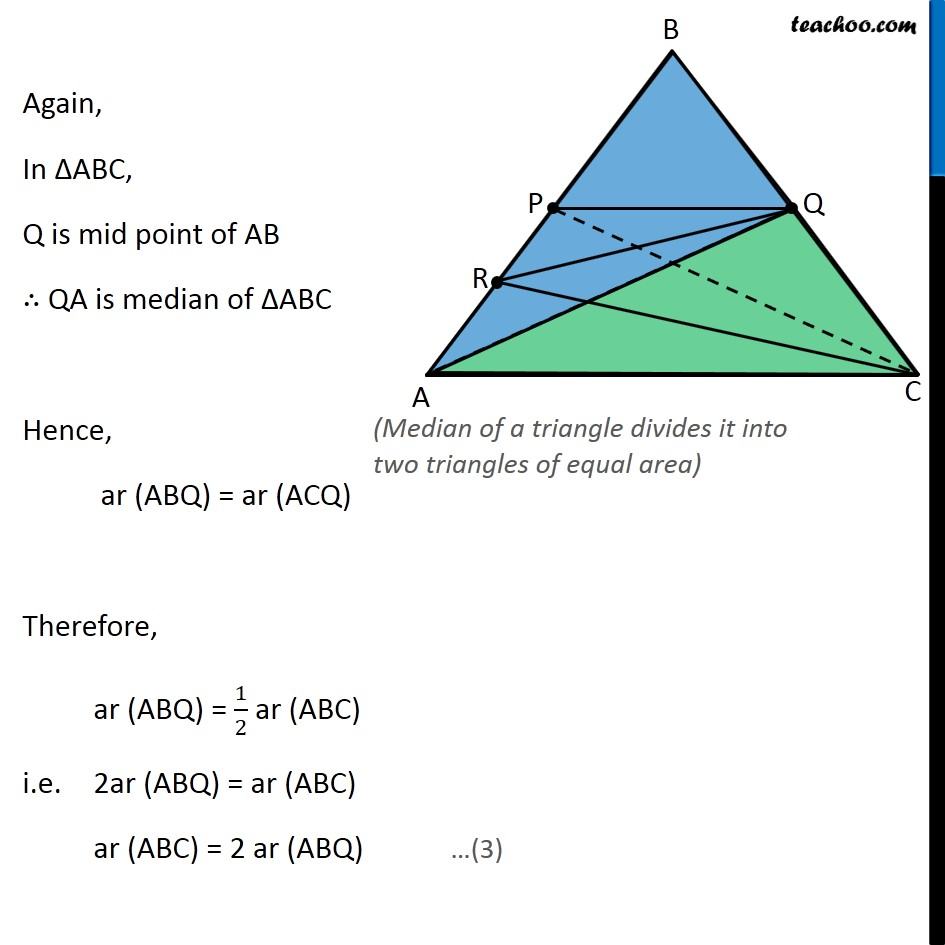
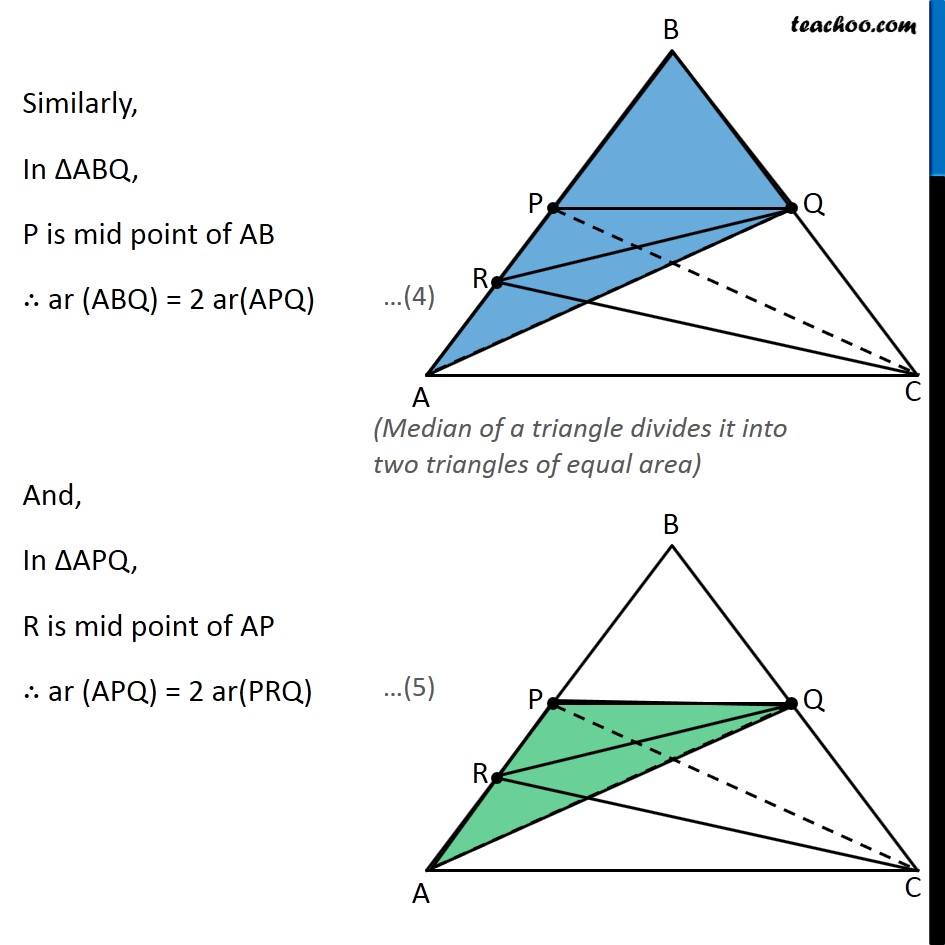
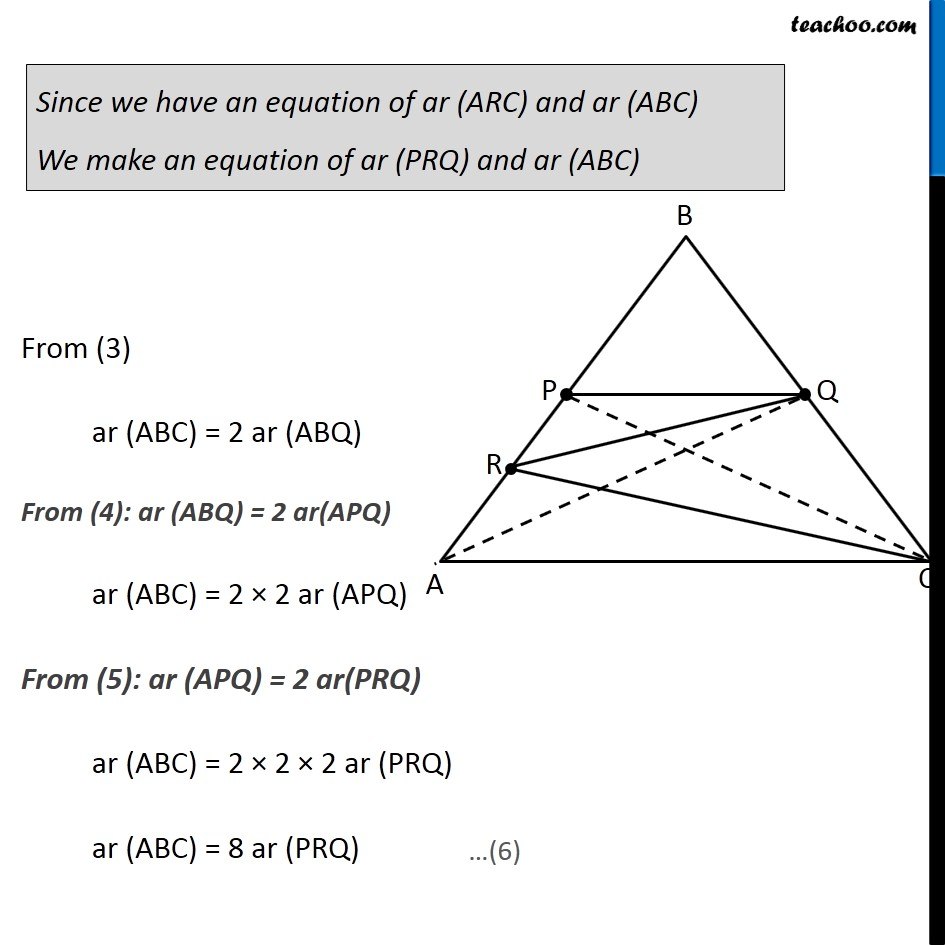
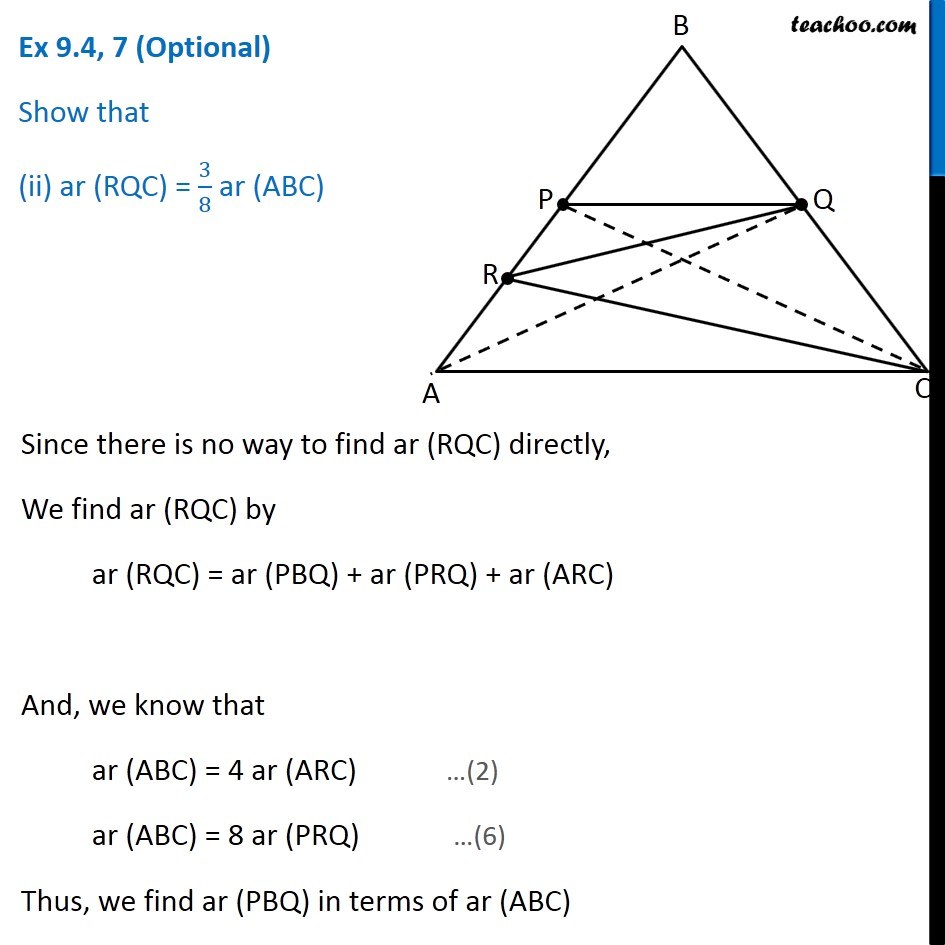
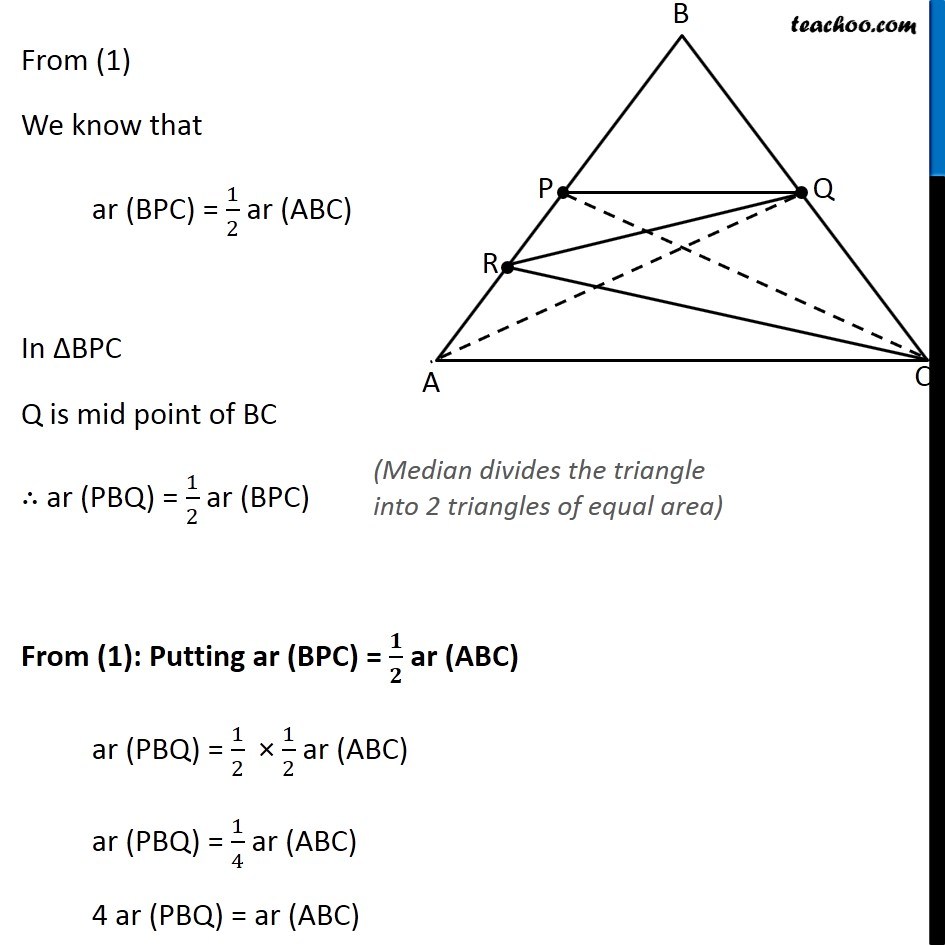
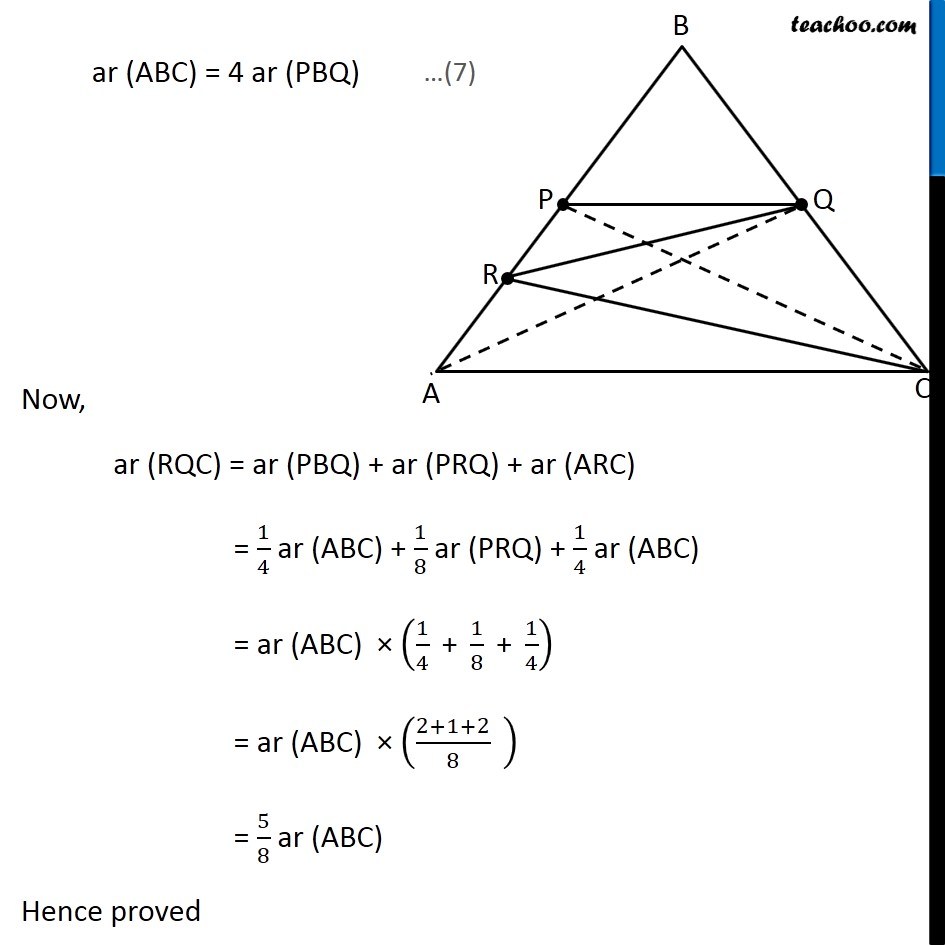
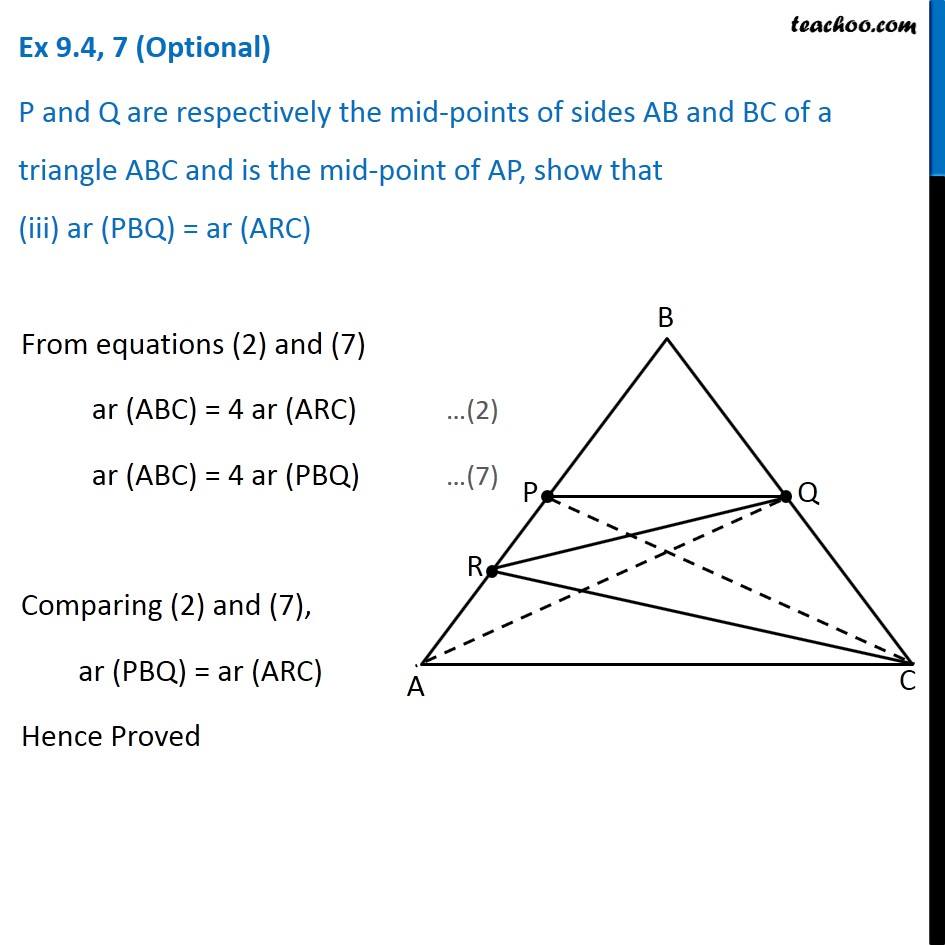
Question 7 P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that (i) ar (PRQ) = 1/2 ar (ARC) In ∆ABC, P is mid point of AB ∴ PC is median of ∆ABC Hence, ar (APC) = ar (BPC) Therefore, ar (APC) = ar (BPC) = 1/2 ar (ABC) (Median of a triangle divides it into two triangles of equal area) Similarly, In ∆APC R is mid Point of PA So, CR is the median of Δ APC Thus, ar (ARC) = 1/2 ar (APC) ar (ARC) = 1/2 × 1/2 ar (ABC) ar (ARC) = 1/4 ar (ABC) 4 ar (ARC) = ar (ABC) ar (ABC) = 4 ar (ARC) From (1): ar (APC) = 1/2 ar (ABC) Again, In ∆ABC, Q is mid point of AB ∴ QA is median of ∆ABC Hence, ar (ABQ) = ar (ACQ) Therefore, ar (ABQ) = 1/2 ar (ABC) i.e. 2ar (ABQ) = ar (ABC) ar (ABC) = 2 ar (ABQ) (Median of a triangle divides it into two triangles of equal area) …(3) Similarly, In ∆ABQ, P is mid point of AB ∴ ar (ABQ) = 2 ar(APQ) And, In ∆APQ, R is mid point of AP ∴ ar (APQ) = 2 ar(PRQ) (Median of a triangle divides it into two triangles of equal area) Since we have an equation of ar (ARC) and ar (ABC) We make an equation of ar (PRQ) and ar (ABC) From (3) ar (ABC) = 2 ar (ABQ) From (4): ar (ABQ) = 2 ar(APQ) ar (ABC) = 2 × 2 ar (APQ) From (5): ar (APQ) = 2 ar(PRQ) ar (ABC) = 2 × 2 × 2 ar (PRQ) ar (ABC) = 8 ar (PRQ) Now, our equations are ar (ABC) = 4 ar (ARC) …(2) ar (ABC) = 8 ar (PRQ) …(6) From (2) & (6), we get 4 ar (ARC) = 8 ar (PRQ) ar (ARC) = 2 ar (PRQ) 1/2 × ar (ARC) = ar (PRQ) ar (ARC) = 1/2 ar (PRQ) Hence proved Question 7 Show that (ii) ar (RQC) = 3/8 ar (ABC) Since there is no way to find ar (RQC) directly, We find ar (RQC) by ar (RQC) = ar (PBQ) + ar (PRQ) + ar (ARC) And, we know that ar (ABC) = 4 ar (ARC) …(2) ar (ABC) = 8 ar (PRQ) …(6) Thus, we find ar (PBQ) in terms of ar (ABC) From (1) We know that ar (BPC) = 1/2 ar (ABC) In ∆BPC Q is mid point of BC ∴ ar (PBQ) = 1/2 ar (BPC) From (1): Putting ar (BPC) = 𝟏/𝟐 ar (ABC) ar (PBQ) = 1/2 × 1/2 ar (ABC) ar (PBQ) = 1/4 ar (ABC) 4 ar (PBQ) = ar (ABC) (Median divides the triangle into 2 triangles of equal area) ar (ABC) = 4 ar (PBQ) Now, ar (RQC) = ar (PBQ) + ar (PRQ) + ar (ARC) = 1/4 ar (ABC) + 1/8 ar (PRQ) + 1/4 ar (ABC) = ar (ABC) × (1/4 " + " 1/8 " + " 1/4) = ar (ABC) × ((2+1+2)/8 " " ) = 5/8 ar (ABC) Hence proved …(7) Question 7 P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and is the mid-point of AP, show that (iii) ar (PBQ) = ar (ARC) From equations (2) and (7) ar (ABC) = 4 ar (ARC) …(2) ar (ABC) = 4 ar (PBQ) …(7) Comparing (2) and (7), ar (PBQ) = ar (ARC) Hence Proved