Theorem 9.1 - Areas of Parallelograms and Triangles

Last updated at April 16, 2024 by

Theorem 9.1 - Parallelograms on same base and between same parallels

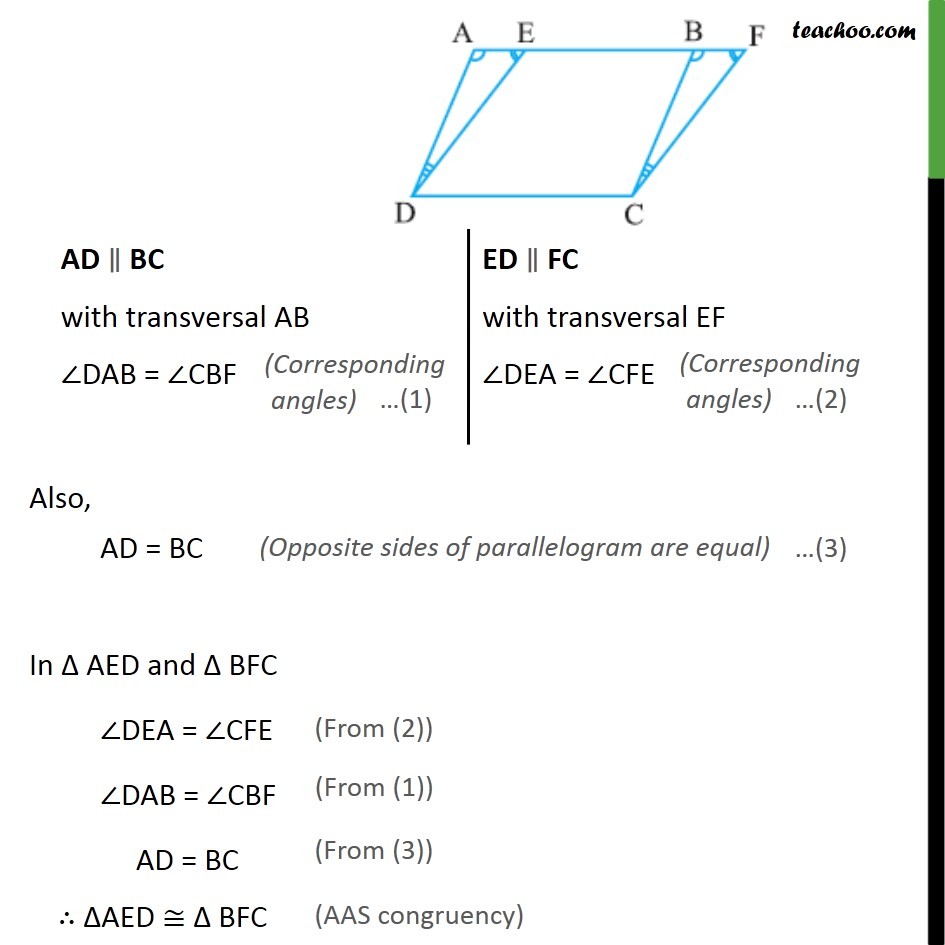
Theorem 9.1 - Chapter 9 Class 9 Areas of Parallelograms and Triangles - Part 2
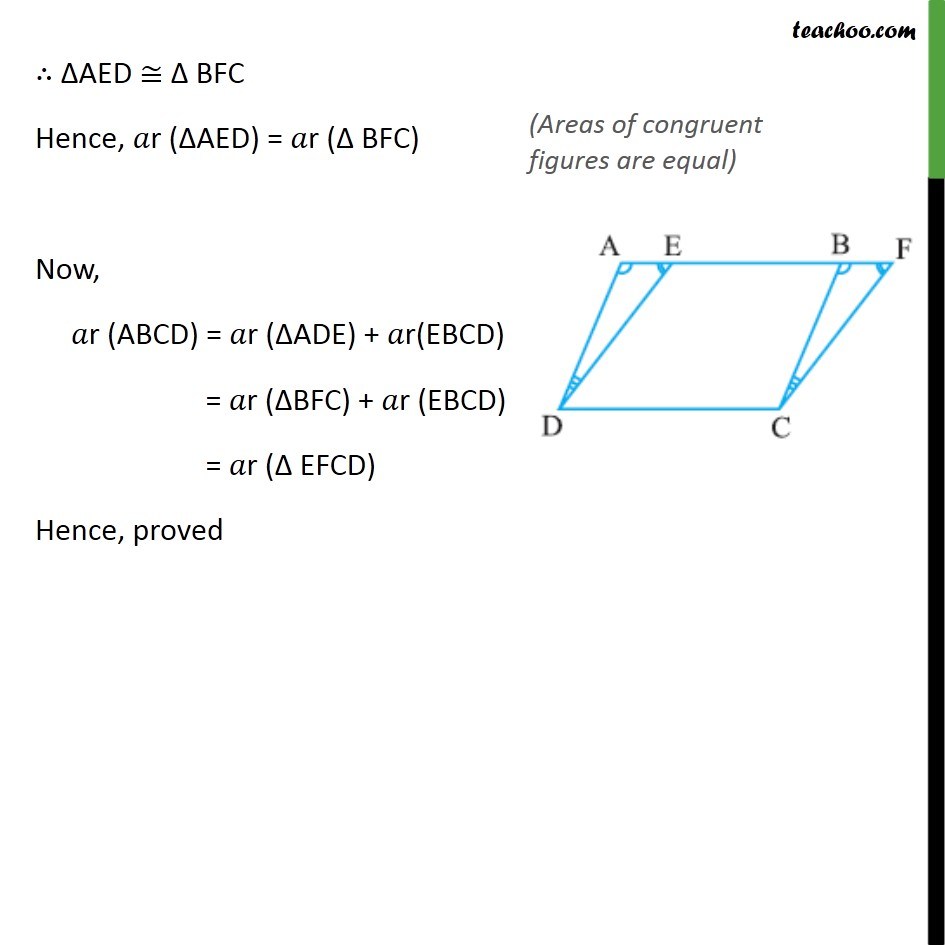
Theorem 9.1 - Chapter 9 Class 9 Areas of Parallelograms and Triangles - Part 3

Go Ad-free

Transcript

Theorem 9.1 Parallelograms on the same base and between the same parallels are equal in area. Given : Two parallelograms ABCD & EFCD, that have the same base CD & lie between same parallels AF & CD. To Prove : r (ABCD) = r (EFCD) Proof : Since opposite sides of parallelogram are parallel Also, AD = BC In AED and BFC DAB = CBF DEA = CFE AD = BC AED BFC AED BFC Hence, r ( AED) = r ( BFC) Now, r (ABCD) = r ( ADE) + r(EBCD) = r ( BFC) + r (EBCD) = r ( EFCD) Hence, proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo