Theorem 9.3 - Areas of Parallelograms and Triangles

Transcript

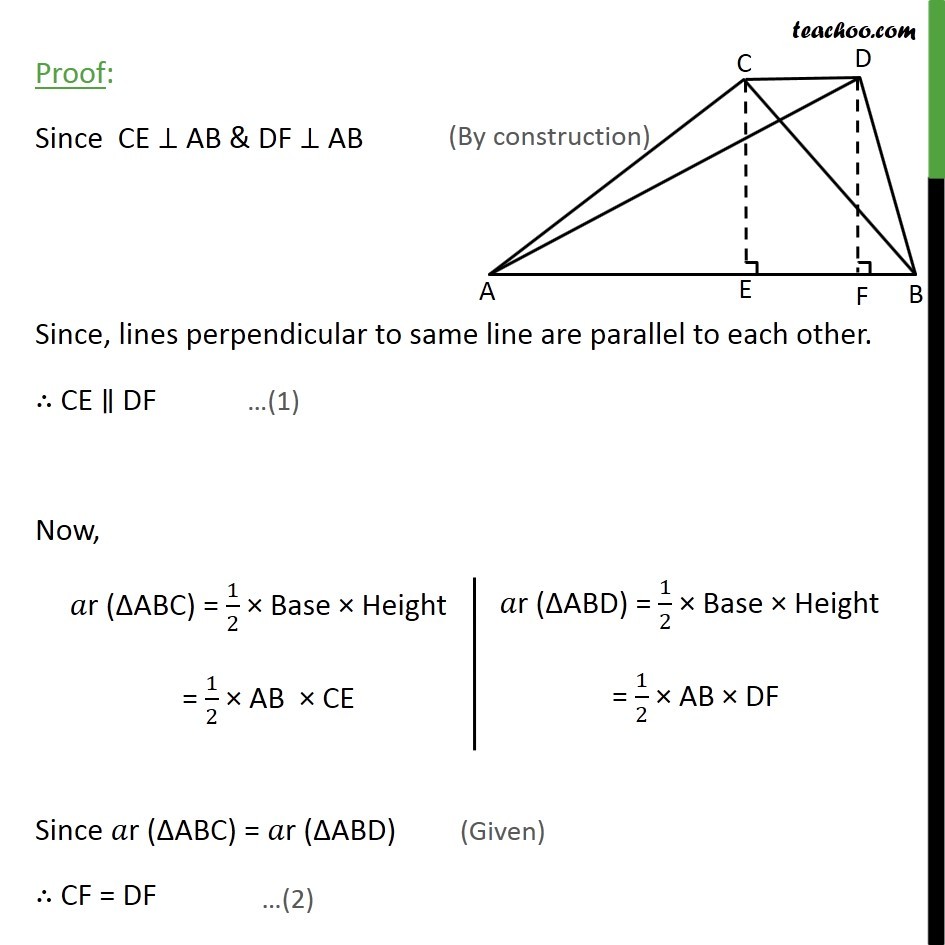
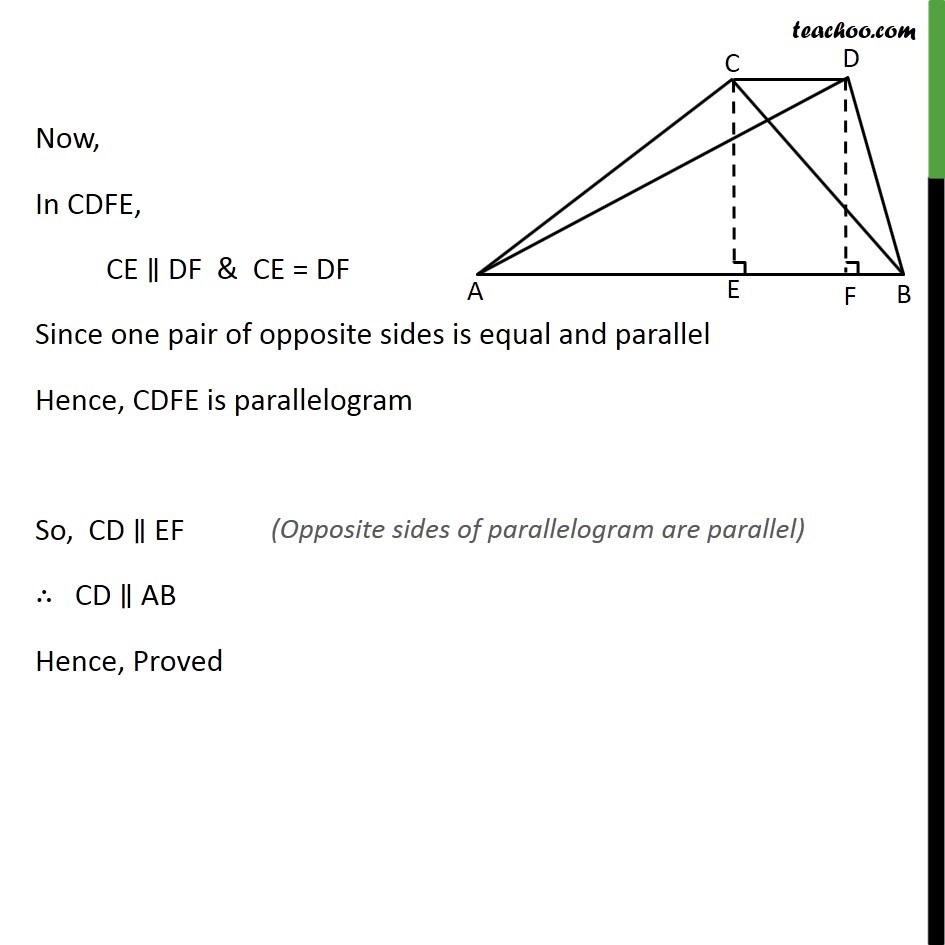
Theorem 9.3 Two triangles having the same base (or equal bases) and equal areas lie between the same parallels. Let us now take some examples to illustrate the use of the above results. Given : ABC and ABD are two triangles on same base AB such that r ( ABC) = r ( ABD). Join CD To Prove : CD AB Construction : Draw the altitudes of ABC and ABD through C and D and meeting base at E and F respectively Proof: Since CE AB & DF AB Since, lines perpendicular to same line are parallel to each other. CE DF Now, Since r ( ABC) = r ( ABD) CF = DF Now, In CDFE, CE DF & CE = DF Since one pair of opposite sides is equal and parallel Hence, CDFE is parallelogram So, CD EF CD AB Hence, Proved