

Last updated at Dec. 16, 2024 by Teachoo




Transcript
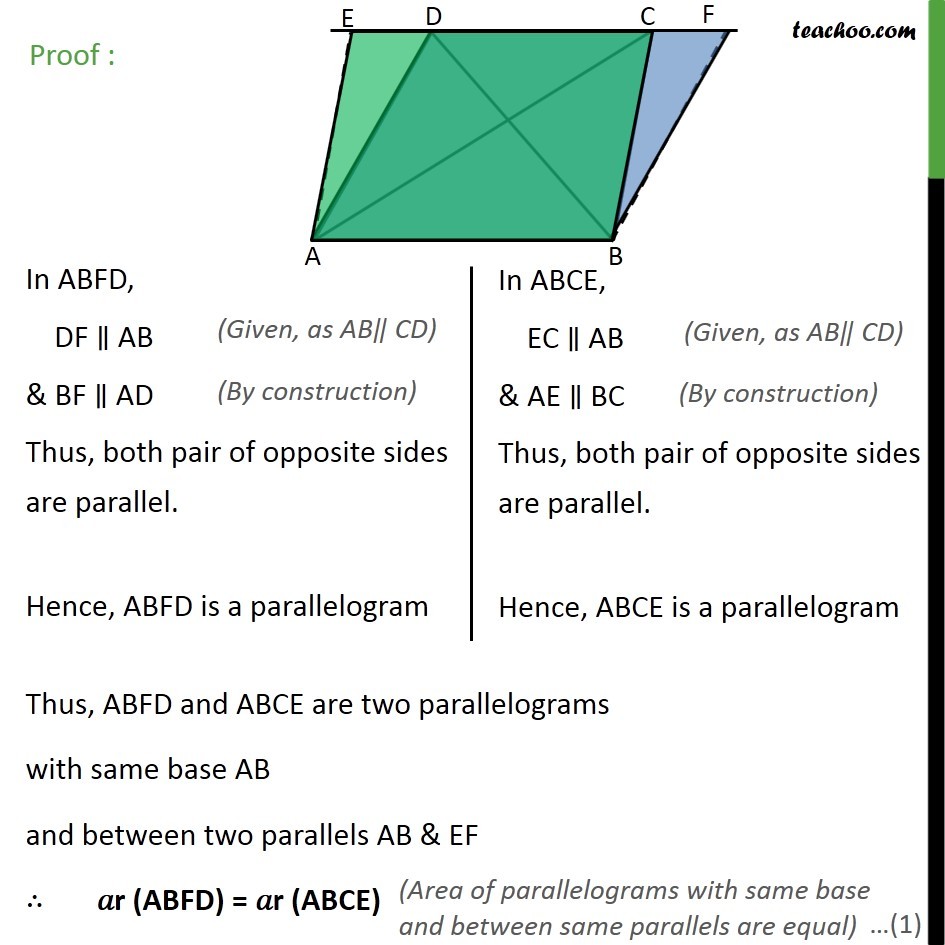
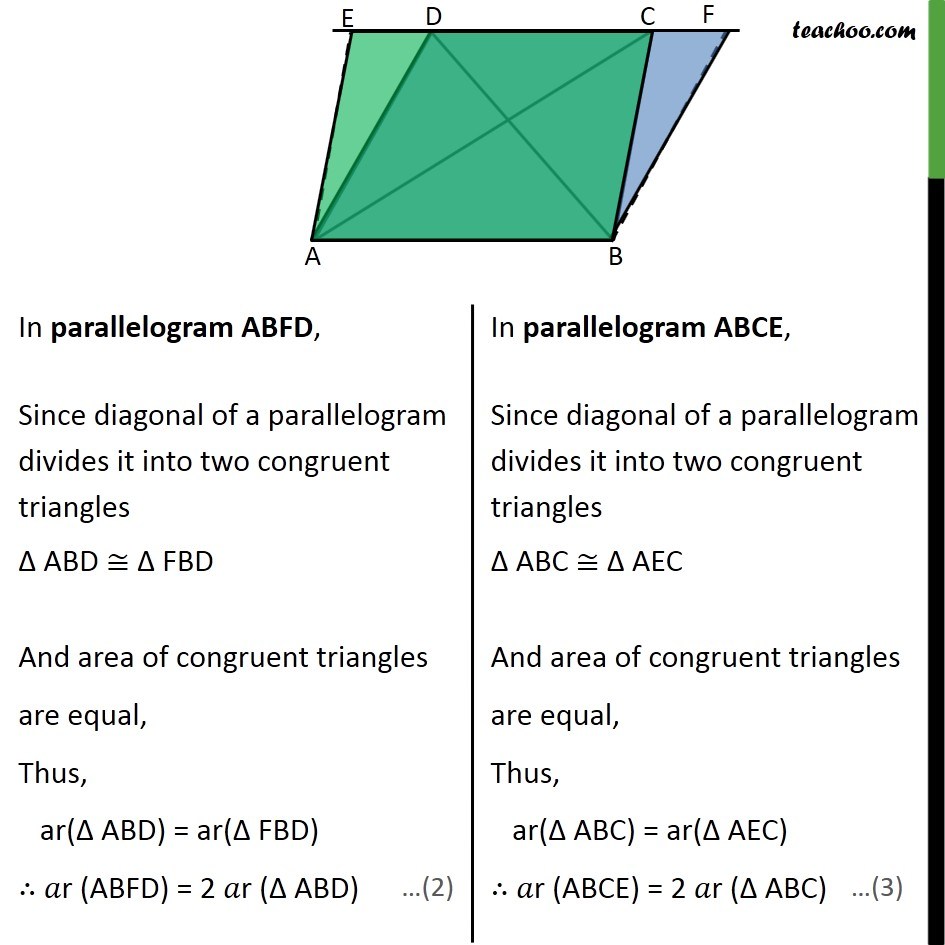
Theorem 9.2 (Method 1) Two triangles on the same base (or equal bases) and between the same parallels are equal in area. Given : ∆ADB and ∆ABC are triangles on same base AB and between the same parallels AB and DC To Prove : 𝑎r (∆ADB) = 𝑎r (∆ABC) Proof: We know that Area of triangle = 1/2×𝐵𝑎𝑠𝑒×𝐻𝑒𝑖𝑔ℎ𝑡 Here AB is base We draw DE ⊥ AB So, DE is the height of ∆ ABD ∴ Area ∆ ABD = 1/2×𝐵𝑎𝑠𝑒×𝐻𝑒𝑖𝑔ℎ𝑡 = 1/2×𝐴𝐵×𝐷𝐸 Here AB, is base We draw CF ⊥ AB So, CF is the height of ∆ ABC ∴ Area ∆ ABC = 1/2×𝐵𝑎𝑠𝑒×𝐻𝑒𝑖𝑔ℎ𝑡 = 1/2×𝐴𝐵×𝐶𝐹 DE & CF are perpendicular between the same parallel line ∴ DE = CF So, from (1) Area ∆ ABD = 1/2×𝐴𝐵×𝐷𝐸 = 1/2×𝐴𝐵×𝐶𝐹 = Area ∆ ABC ∴ Area ∆ ABD = Area of ∆ ABC Hence proved. Theorem 9.2 Two triangles on the same base (or equal bases) and between the same parallels are equal in area. Given : ∆ADB and ∆ABC are triangles on same base AB and between the same parallels AB and DC To Prove : 𝑎r (∆ADB) = 𝑎r (∆ABC) Construction : Construct a line through A parallel to be meeting DC at E i.e. AE ∥ BC & Construct a line through B parallel to AD meeting DC at F i.e. BF ∥ AD Proof : From (1) 𝑎r (ABFD) = 𝑎r (ABCE) 2 𝑎r (∆ABD) = 2 𝑎r (∆ABC) 𝑎r (∆ABD) = 𝑎r (∆ABC) Hence, proved