Question 6 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

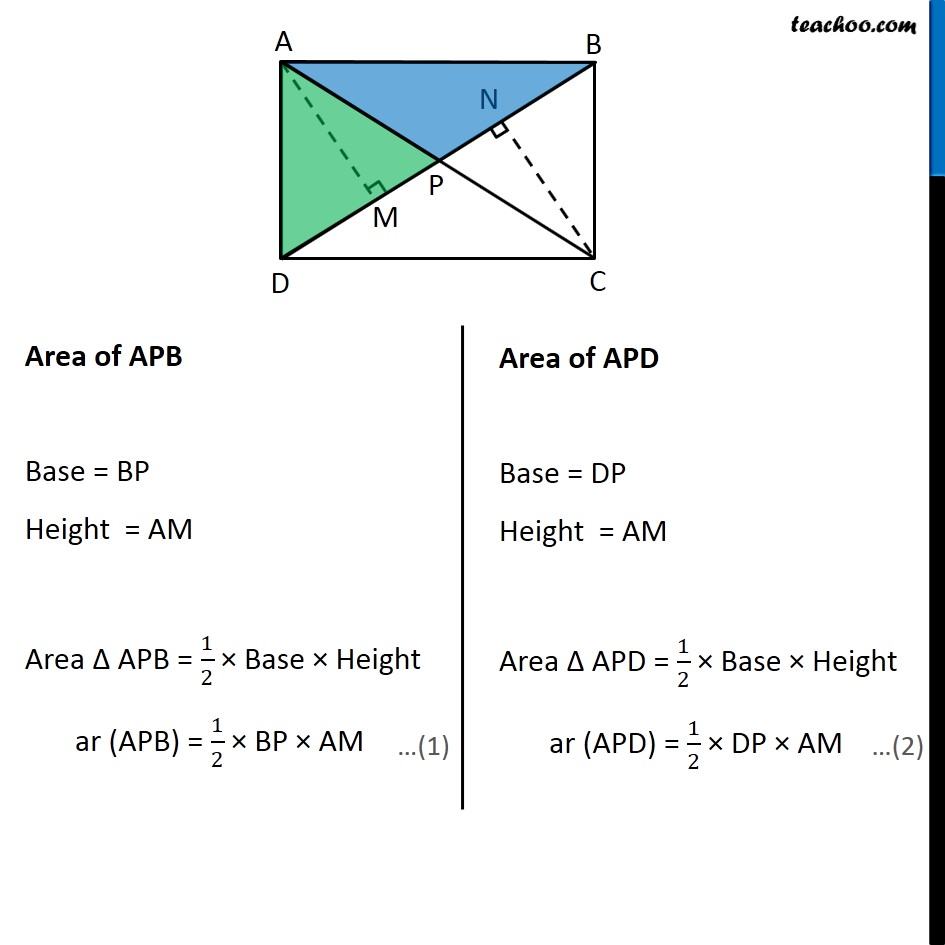
Question 6 Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC). [Hint : From A and C, draw perpendiculars to BD.] Given: A quadrilateral ABCD To prove: A quadrilateral ABCD Construction: Draw AM ⊥ BD and CN ⊥ BD Proof: Finding Area of Δ APB and Δ APD Area of APB Base = BP Height = AM Area Δ APB = 1/2 × Base × Height ar (APB) = 1/2 × BP × AM Area of APD Base = DP Height = AM Area Δ APD = 1/2 × Base × Height ar (APD) = 1/2 × DP × AM Dividing by (1) by (2) (𝑎𝑟 (𝐴𝑃𝐵))/(𝑎𝑟 (𝐴𝑃𝐷)) = (1/2 × 𝐵𝑃 × 𝐴𝑀)/(1/2 × 𝐷𝑃 × 𝐴𝑀) (𝑎𝑟 (𝐴𝑃𝐵))/(𝑎𝑟 (𝐴𝑃𝐷)) = 𝐵𝑃/𝐷𝑃 …(3) Area of BPC Base = BP Height = CN Area Δ BPC = 1/2 × Base × Height ar (BPC) = 1/2 × BP × CN Area of CPD Base = DP Height = CN Area Δ CPD = 1/2 × Base × Height ar (CPD) = 1/2 × DP × CN Dividing by (4) by (5) (𝑎𝑟 (𝐵𝑃𝐶))/(𝑎𝑟 (𝐶𝑃𝐷)) = (1/2 × 𝐵𝑃 × 𝐶𝑁)/(1/2 × 𝐷𝑃 × 𝐶𝑁) (𝑎𝑟 (𝐵𝑃𝐶))/(𝑎𝑟 (𝐶𝑃𝐷)) = 𝐵𝑃/(𝐷𝑃 ) From (3) and (6) (𝑎𝑟 (𝐴𝑃𝐵))/(𝑎𝑟 (𝐴𝑃𝐷)) = (𝑎𝑟 (𝐵𝑃𝐶))/(𝑎𝑟 (𝐶𝑃𝐷)) ar (APB) × ar (CPD) = ar (APD) × ar (BPC) Hence Proved.