Question 5 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

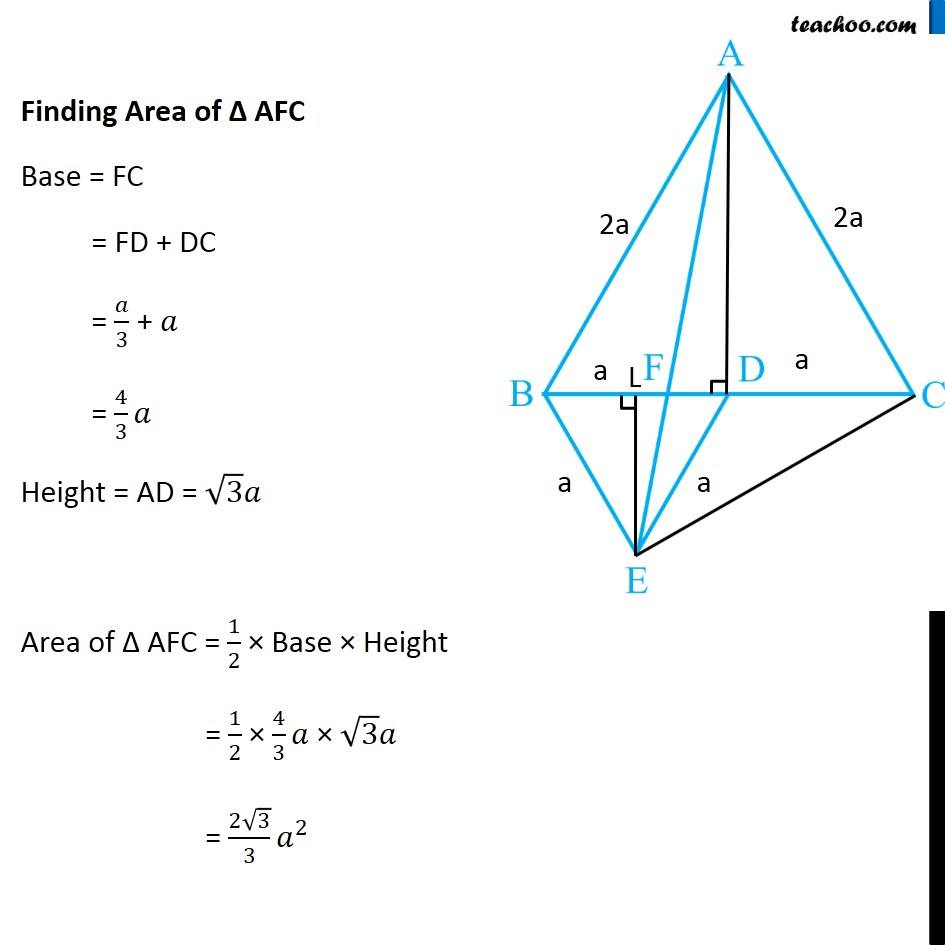
Transcript

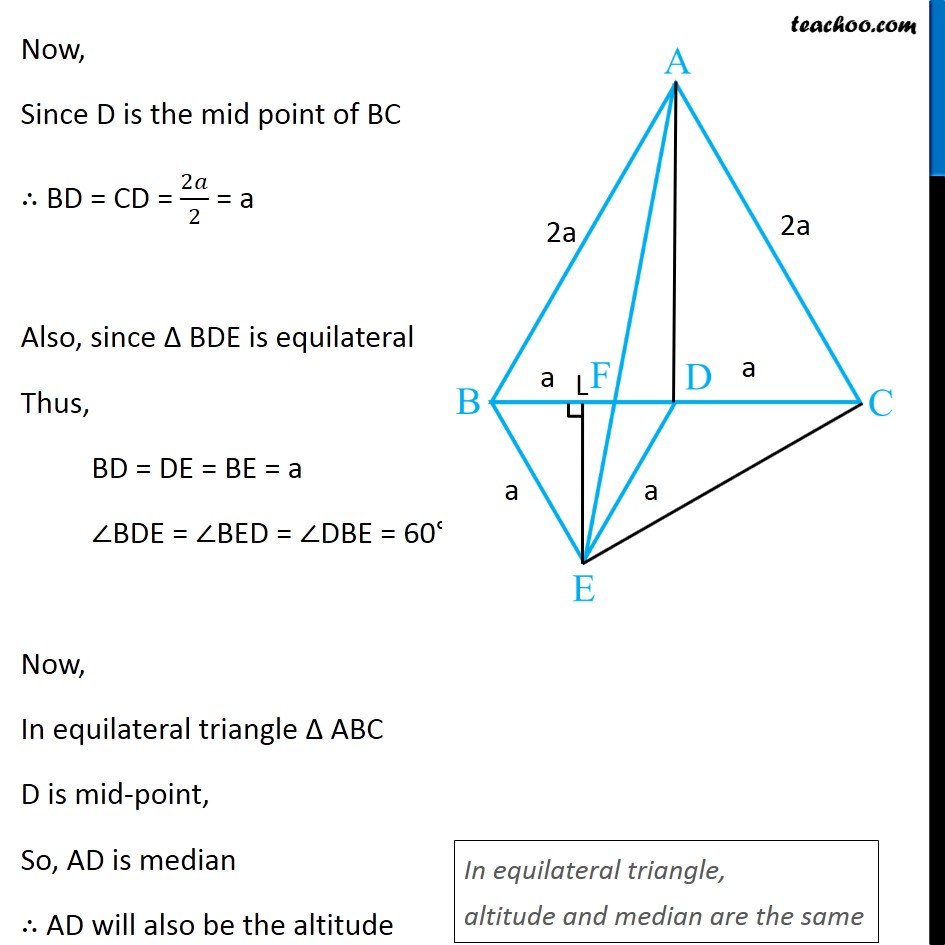
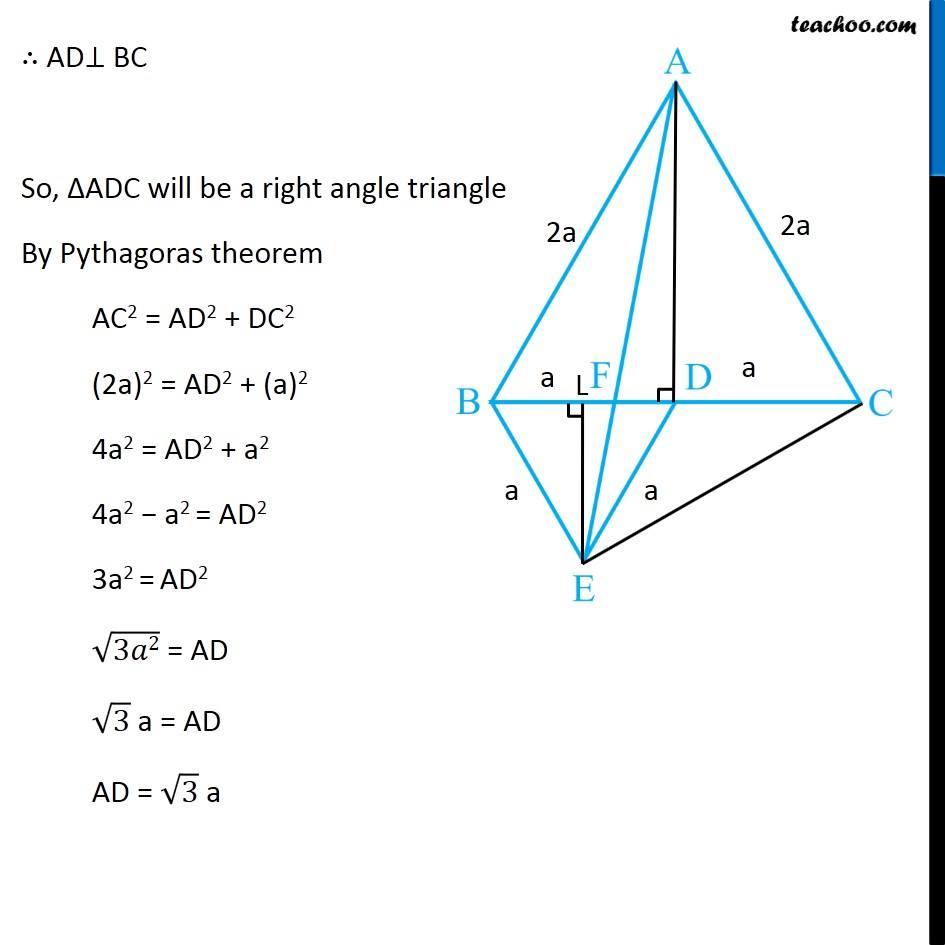
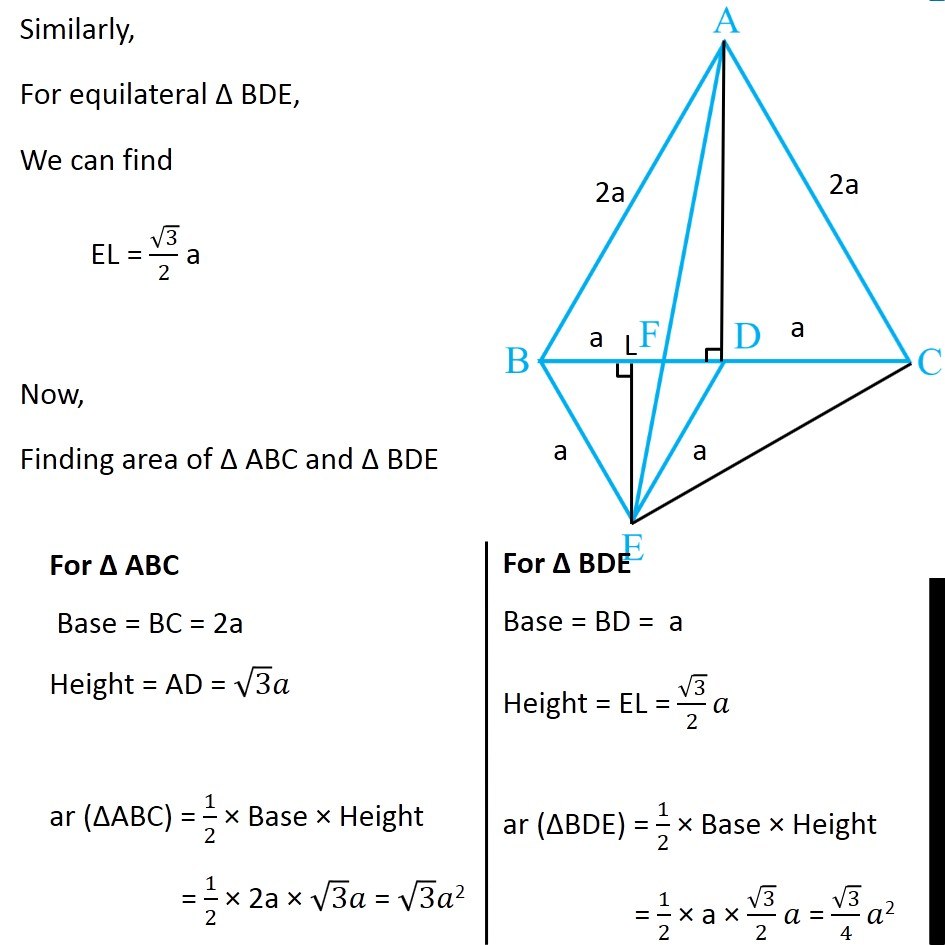
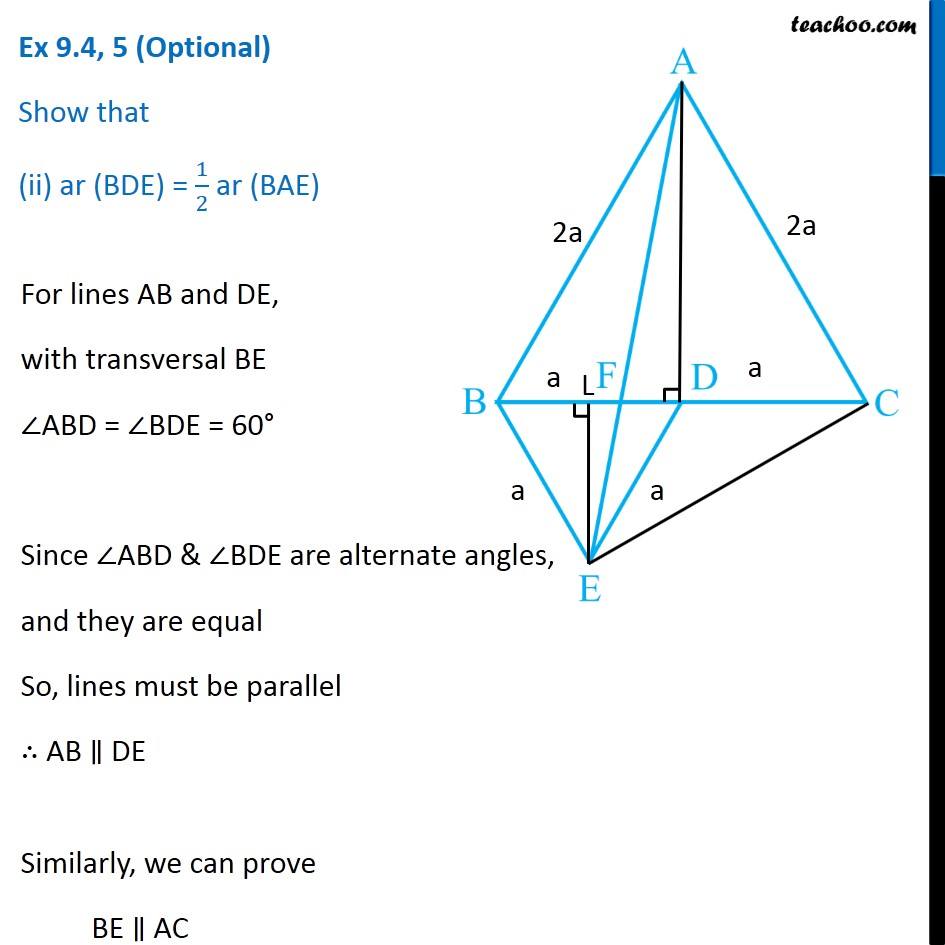
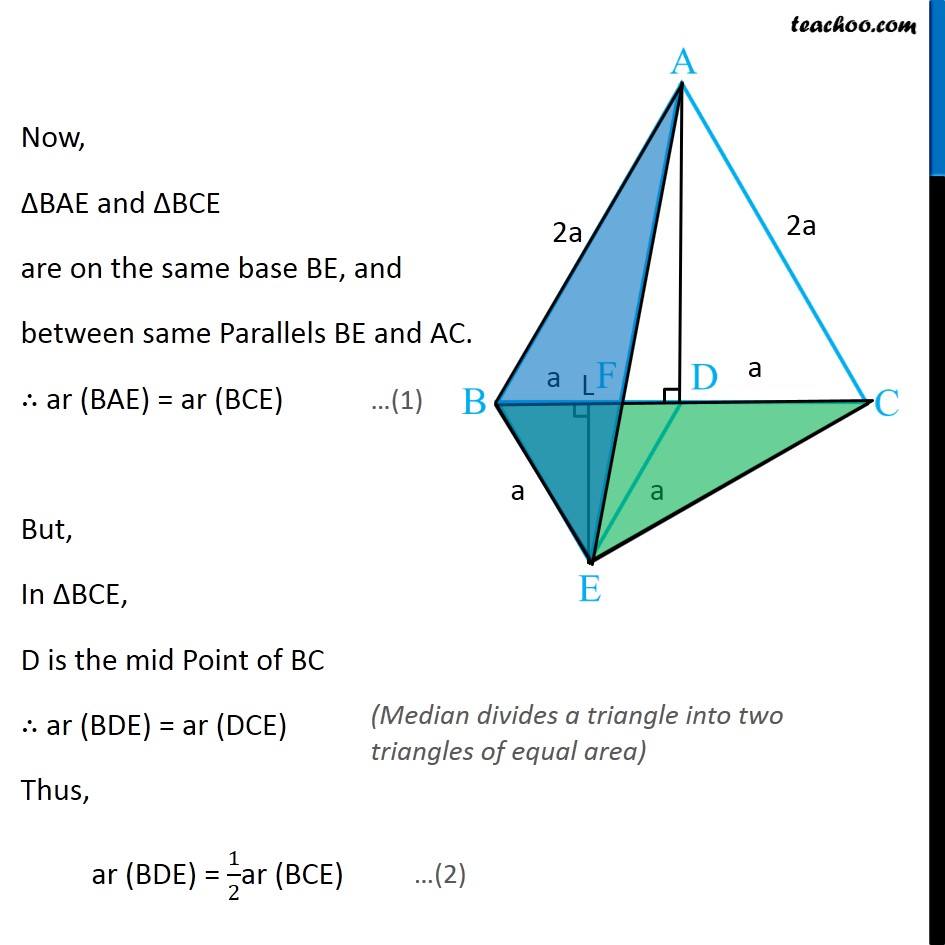
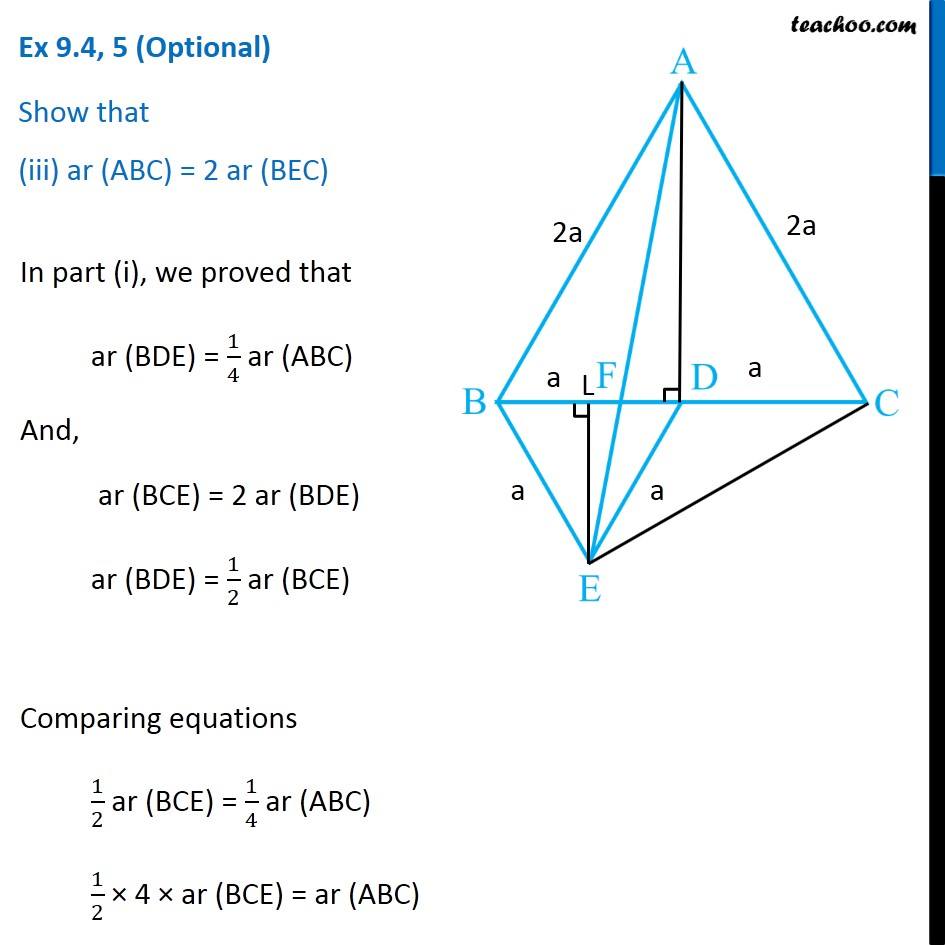
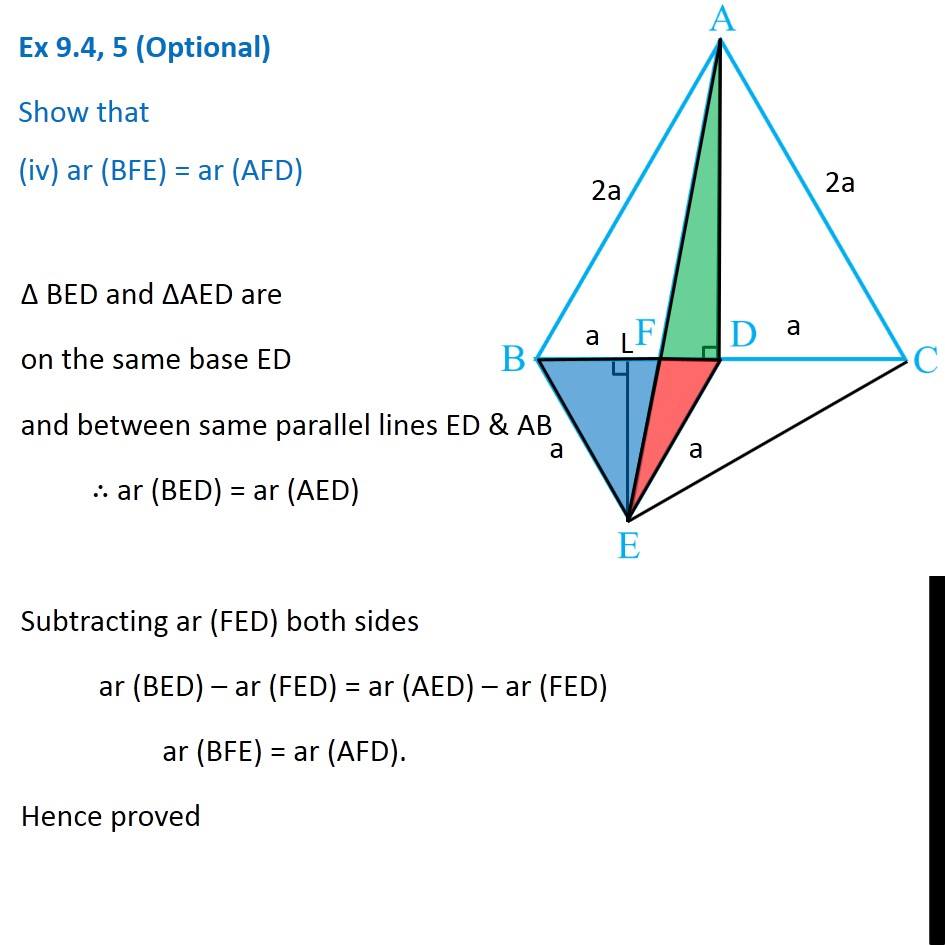
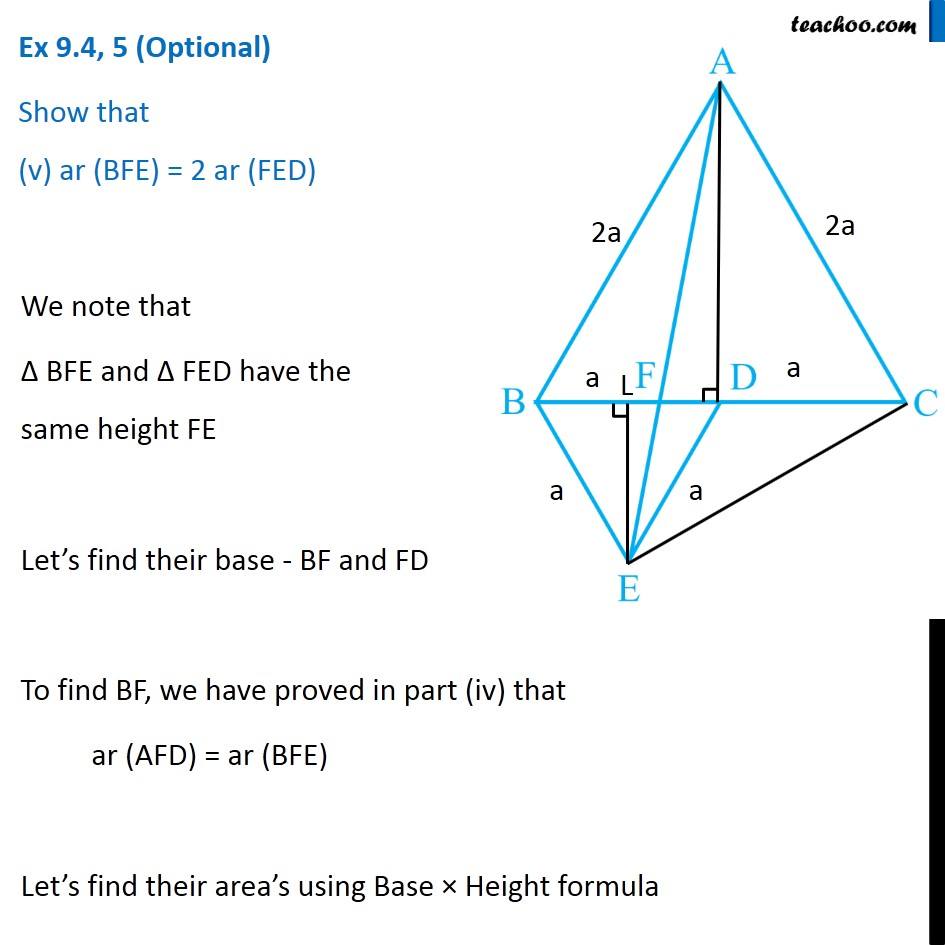
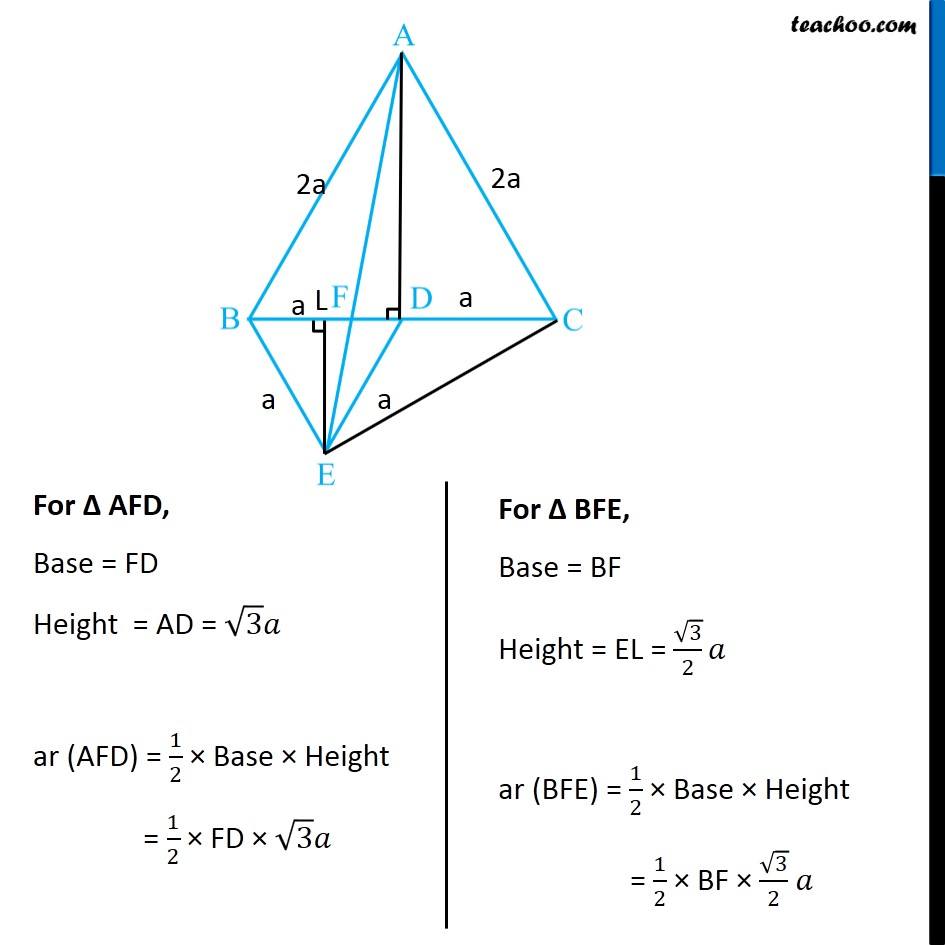
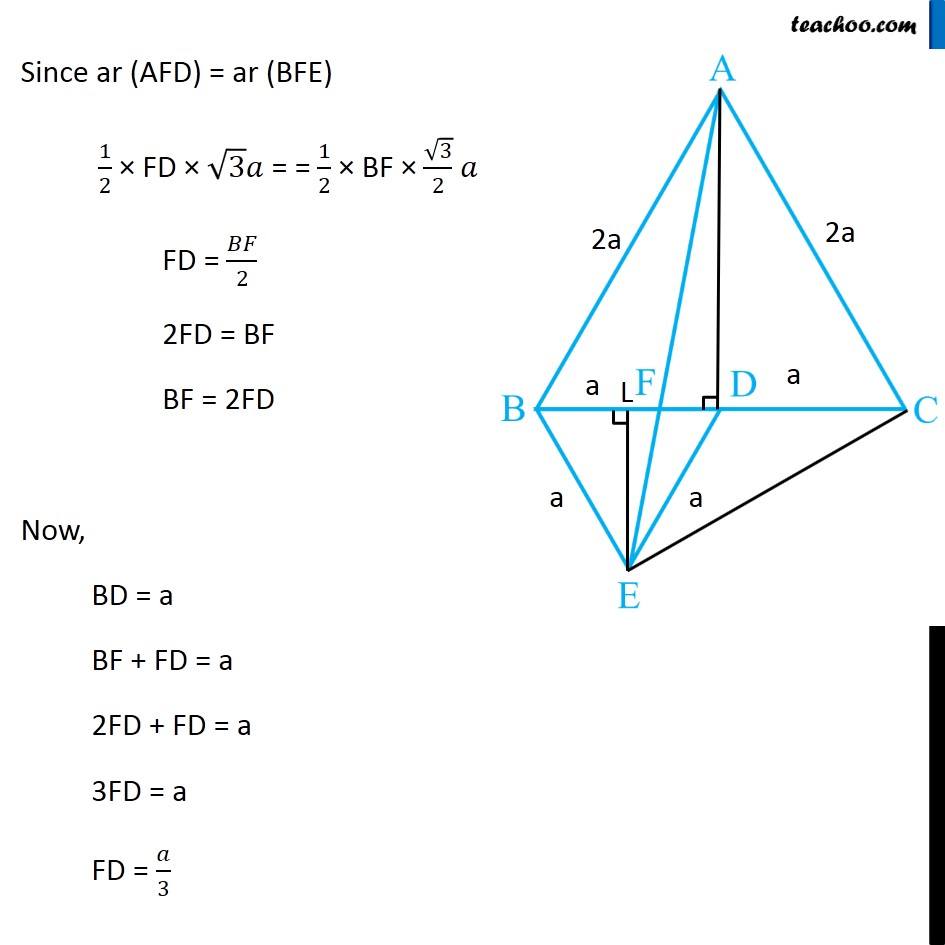
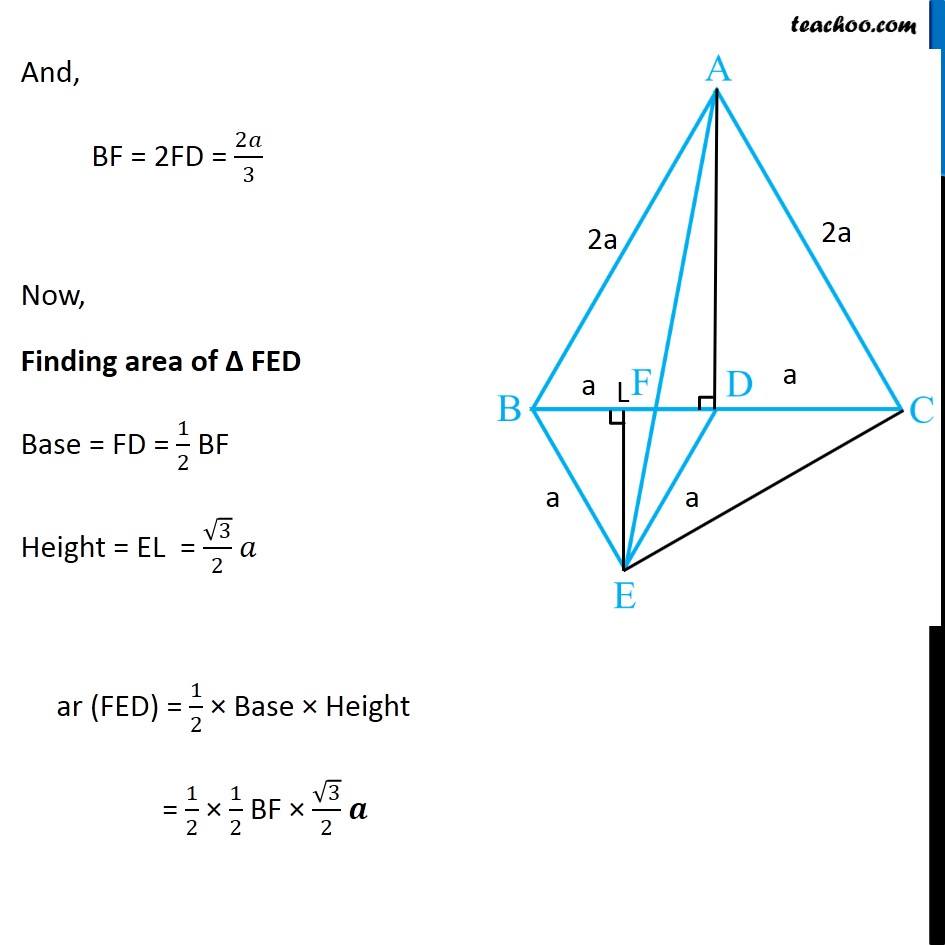
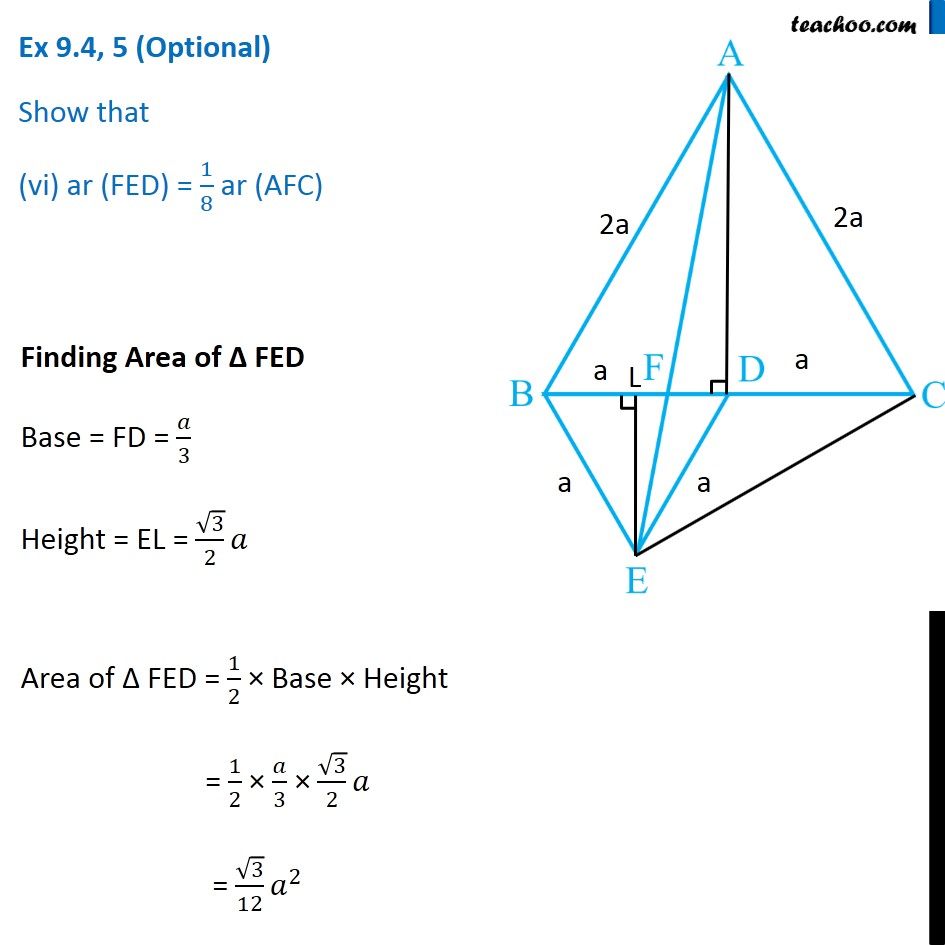
Question 5 In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (i) ar (BDE) = 1/4 ar (ABC) [Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.] Join EC and AD. Draw EL ⊥ BD. Given ∆ABC is an equilateral triangle, Let AB = BC = AC = 2a & ∠BAC = ∠ABC = ∠ACB = 60° Now, Since D is the mid point of BC ∴ BD = CD = 2𝑎/2 = a Also, since Δ BDE is equilateral Thus, BD = DE = BE = a ∠BDE = ∠BED = ∠DBE = 60° Now, In equilateral triangle Δ ABC D is mid-point, So, AD is median ∴ AD will also be the altitude In equilateral triangle, altitude and median are the same ∴ AD⊥ BC So, ∆ADC will be a right angle triangle By Pythagoras theorem AC2 = AD2 + DC2 (2a)2 = AD2 + (a)2 4a2 = AD2 + a2 4a2 − a2 = AD2 3a2 = AD2 √3𝑎2 = AD √3 a = AD AD = √3 a Similarly, For equilateral Δ BDE, We can find EL = √3/2 a Now, Finding area of Δ ABC and Δ BDE For ∆ ABC Base = BC = 2a Height = AD = √3 𝑎 ar (∆ABC) = 1/2 × Base × Height = 1/2 × 2a × √3 𝑎 = √3 𝑎2 For ∆ BDE Base = BD = a Height = EL = √3/2 𝑎 ar (∆BDE) = 1/2 × Base × Height = 1/2 × a × √3/2 𝑎 = √3/4 𝑎2 Now, (𝑎𝑟 (𝐵𝐷𝐸))/(𝑎𝑟 (𝐴𝐵𝐶)) = (√3/4 𝑎"2" )/(√3 𝑎"2" ) (𝑎𝑟 (𝐵𝐷𝐸))/(𝑎𝑟 (𝐴𝐵𝐶)) = (√3 𝑎"2" )/(√3 𝑎"2" ) × 1/4 (𝑎𝑟 (𝐵𝐷𝐸))/(𝑎𝑟 (𝐴𝐵𝐶)) = 1/4 ar (BDE) = 1/4 ar (ABC) Hence proved Question 5 Show that (ii) ar (BDE) = 1/2 ar (BAE) For lines AB and DE, with transversal BE ∠ABD = ∠BDE = 60° Since ∠ABD & ∠BDE are alternate angles, and they are equal So, lines must be parallel ∴ AB ∥ DE Similarly, we can prove BE ∥ AC Now, ∆BAE and ∆BCE are on the same base BE, and between same Parallels BE and AC. ∴ ar (BAE) = ar (BCE) But, In ∆BCE, D is the mid Point of BC ∴ ar (BDE) = ar (DCE) Thus, ar (BDE) = 1/2ar (BCE) (Median divides a triangle into two triangles of equal area) …(2) From (1) & 2 ar (BDE) = 1/2 ar (BAE) Hence proved Question 5 Show that (iii) ar (ABC) = 2 ar (BEC) In part (i), we proved that ar (BDE) = 1/4 ar (ABC) And, ar (BCE) = 2 ar (BDE) ar (BDE) = 1/2 ar (BCE) Comparing equations 1/2 ar (BCE) = 1/4 ar (ABC) 1/2 × 4 × ar (BCE) = ar (ABC) 2 ar (BCE) = ar (ABC) ar (ABC) = 2ar (BCE) Hence proved Question 5 Show that (iv) ar (BFE) = ar (AFD) ∆ BED and ∆AED are on the same base ED and between same parallel lines ED & AB ∴ ar (BED) = ar (AED) Subtracting ar (FED) both sides ar (BED) – ar (FED) = ar (AED) – ar (FED) ar (BFE) = ar (AFD). Hence proved Question 5 Show that (v) ar (BFE) = 2 ar (FED) We note that Δ BFE and Δ FED have the same height FE Let’s find their base - BF and FD To find BF, we have proved in part (iv) that ar (AFD) = ar (BFE) Let’s find their area’s using Base × Height formula For ∆ AFD, Base = FD Height = AD = √3 𝑎 ar (AFD) = 1/2 × Base × Height = 1/2 × FD × √3 𝑎 For ∆ BFE, Base = BF Height = EL = √3/2 𝑎 ar (BFE) = 1/2 × Base × Height = 1/2 × BF × √3/2 𝑎 Since ar (AFD) = ar (BFE) 1/2 × FD × √3 𝑎 = = 1/2 × BF × √3/2 𝑎 FD = 𝐵𝐹/2 2FD = BF BF = 2FD Now, BD = a BF + FD = a 2FD + FD = a 3FD = a FD = 𝑎/3 And, BF = 2FD = 2𝑎/3 Now, Finding area of ∆ FED Base = FD = 1/2 BF Height = EL = √3/2 𝑎 ar (FED) = 1/2 × Base × Height = 1/2 × 1/2 BF × √3/2 𝒂 Now, (𝑎𝑟 (𝐵𝐹𝐸))/(𝑎𝑟 (𝐹𝐸𝐷)) = (1/2 × 𝐵𝐹 × √3/2 " " 𝑎" " )/(1/2 × 1/2 𝐵𝐹 × √3/2 " " 𝑎) (𝑎𝑟 (𝐵𝐹𝐸))/(𝑎𝑟 (𝐹𝐸𝐷)) = 1/(1/2) (𝑎𝑟 (𝐵𝐹𝐸))/(𝑎𝑟 (𝐹𝐸𝐷)) = 2 ar (BFE) = 2 ar (FED) Hence proved Question 5 Show that (vi) ar (FED) = 1/8 ar (AFC) Finding Area of Δ FED Base = FD = 𝑎/3 Height = EL = √3/2 𝑎 Area of Δ FED = 1/2 × Base × Height = 1/2 × 𝑎/3 × √3/2 𝑎 = √3/12 𝑎^2 Finding Area of Δ AFC Base = FC = FD + DC = 𝑎/3 + 𝑎 = 4/3 𝑎 Height = AD = √3 𝑎 Area of Δ AFC = 1/2 × Base × Height = 1/2 × 4/3 𝑎 × √3 𝑎 = (2√3)/3 𝑎^2 Now (𝑎𝑟 (𝐹𝐸𝐷))/(𝑎𝑟 (𝐴𝐹𝐶)) = (√3/12 𝑎^2)/((2√3)/3 𝑎^2 ) (𝑎𝑟 (𝐹𝐸𝐷))/(𝑎𝑟 (𝐴𝐹𝐶)) =√3/12 𝑎^2×3/(2√3 𝑎^2 ) (𝑎𝑟 (𝐹𝐸𝐷))/(𝑎𝑟 (𝐴𝐹𝐶)) = 1/12×3/2 (𝑎𝑟 (𝐹𝐸𝐷))/(𝑎𝑟 (𝐴𝐹𝐶)) = 1/8 ar (FED) = 1/8 ar (AFC) Hence Proved