Question 2 - Area of Triangles - Areas of Parallelograms and Triangles

Transcript

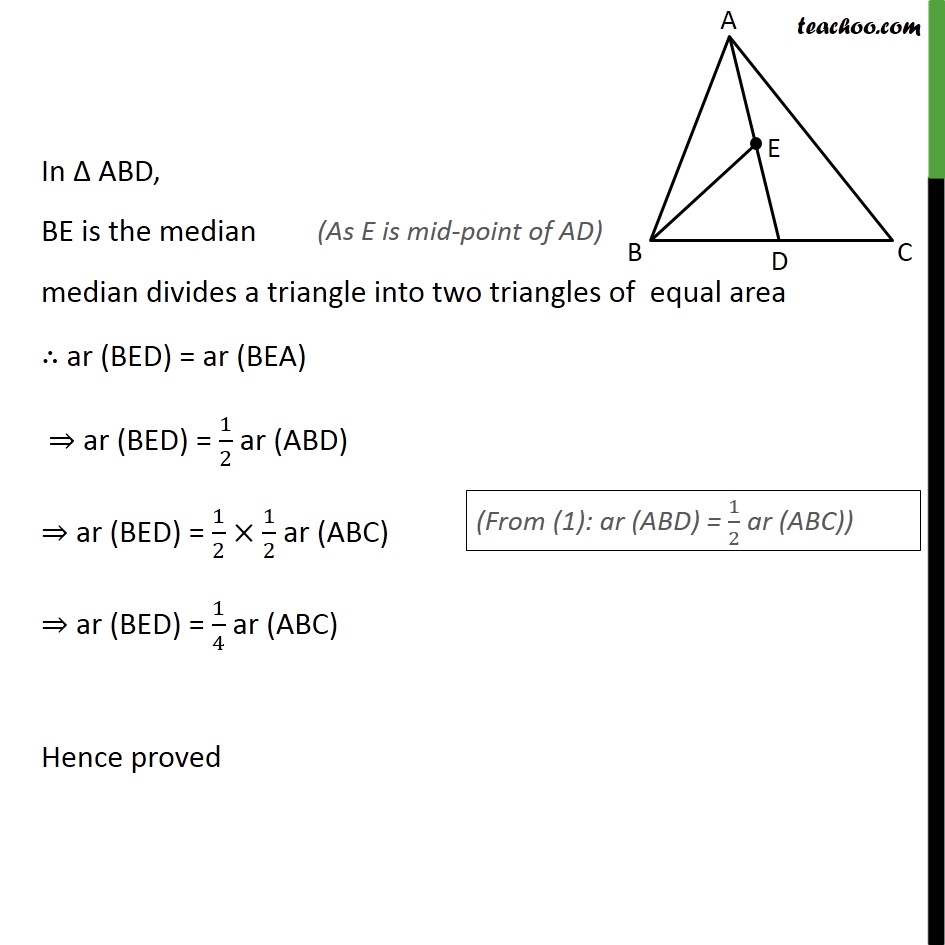
Question 2 In a triangle ABC , E is the mid-point of median AD show that ar(BED) = 1/4 ar (ABC). Given: Δ ABC, with AD as median i.e. BD = CD & E is the mid-point of AD, i.e., AE = DE To prove: ar (BED) = 1/4 ar (ABC). Proof : AD is a median of Δ ABC & median divides a triangle into two triangles of equal area ∴ ar (ABD) = ar (ACD) ⇒ ar (ABD) = 1/2 ar (ABC) In Δ ABD, BE is the median median divides a triangle into two triangles of equal area ∴ ar (BED) = ar (BEA) ⇒ ar (BED) = 1/2 ar (ABD) ⇒ ar (BED) = 1/2× 1/2 ar (ABC) ⇒ ar (BED) = 1/4 ar (ABC) Hence proved