Question 4 - Area of Triangles - Areas of Parallelograms and Triangles

Last updated at April 16, 2024 by

Ex 9.3, 4 - In figure, ABC and ABD are two triangles - Median divides triangle into two triangles of equal area

Ex 9.3, 4 - Chapter 9 Class 9 Areas of Parallelograms and Triangles - Part 2

Transcript

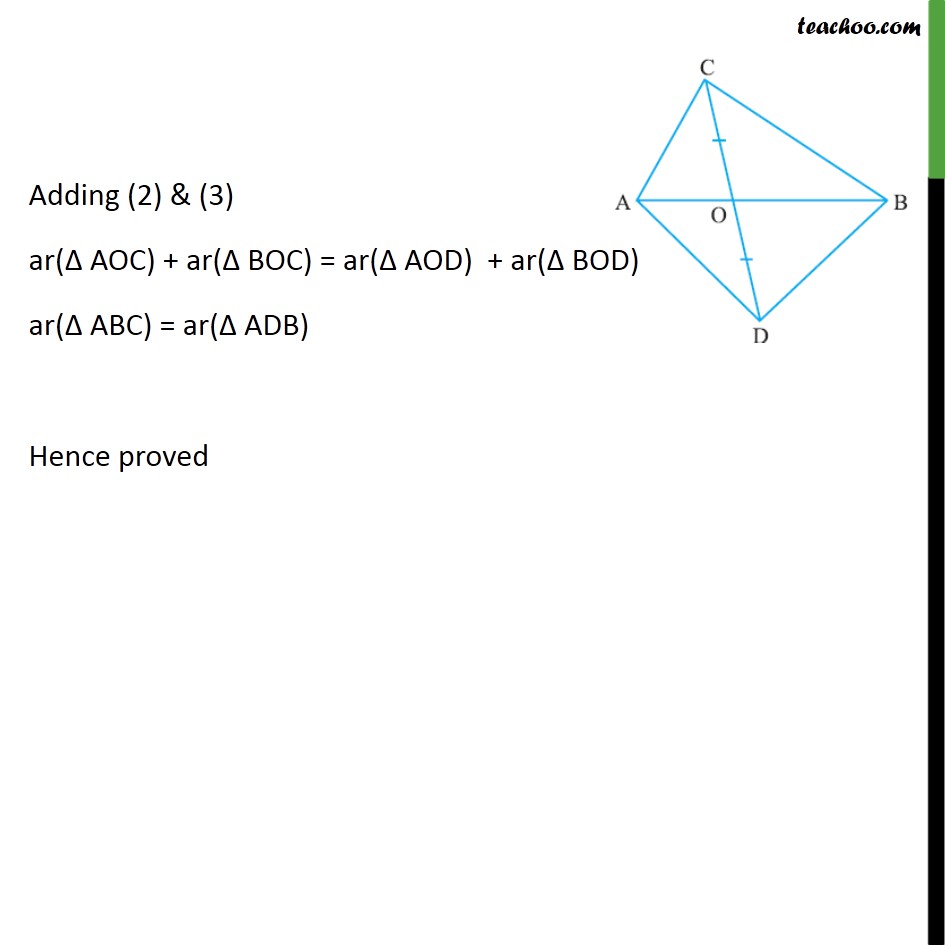
Question 4 In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD). Given: ΔABC and ΔABD on the same base AB & AB bisects CD, i.e. , OC = OD To prove: ar (ABC) = ar (ABD) Proof : In Δ ACD, Since OC = OD ∴ OA is the median. ⇒ ar(Δ AOC) = ar(Δ AOD) Similarly , in Δ BCD Since OC = OD ∴ OB is the median ⇒ ar(Δ BOC) = ar(Δ BOD) Adding (2) & (3) ar(Δ AOC) + ar(Δ BOC) = ar(Δ AOD) + ar(Δ BOD) ar(Δ ABC) = ar(Δ ADB) Hence proved

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.