Misc 23 - Chapter 9 Class 11 Straight Lines

Transcript

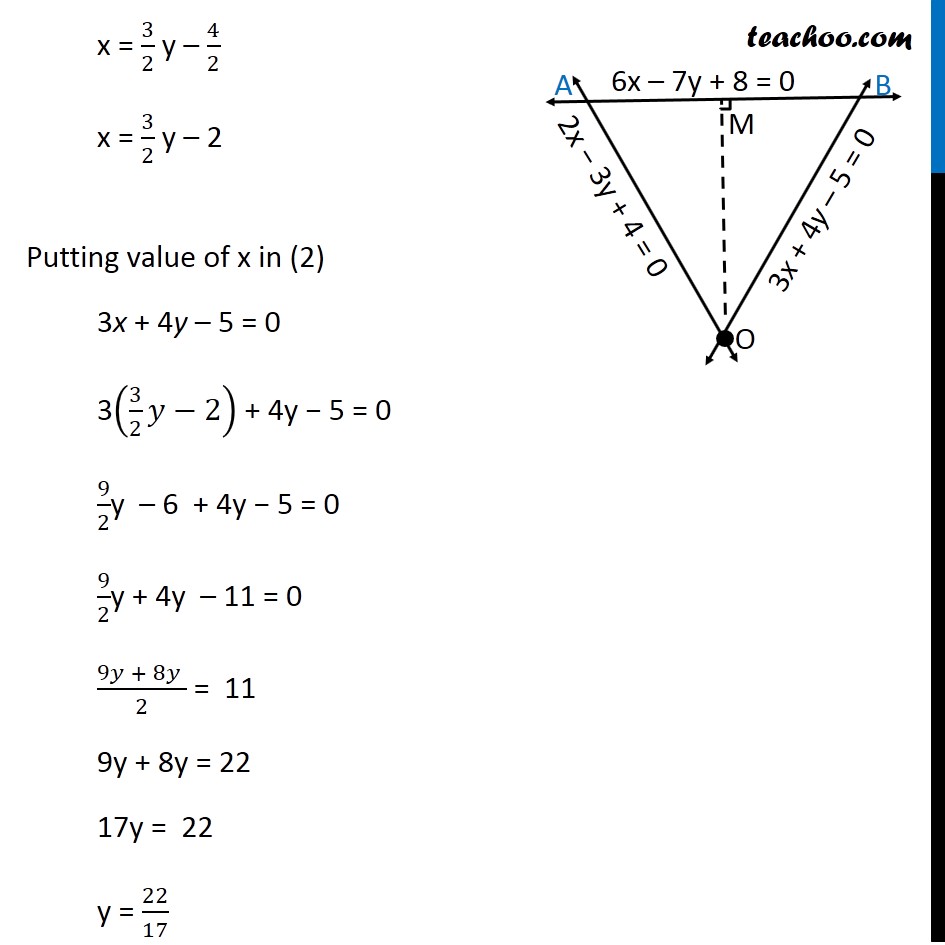
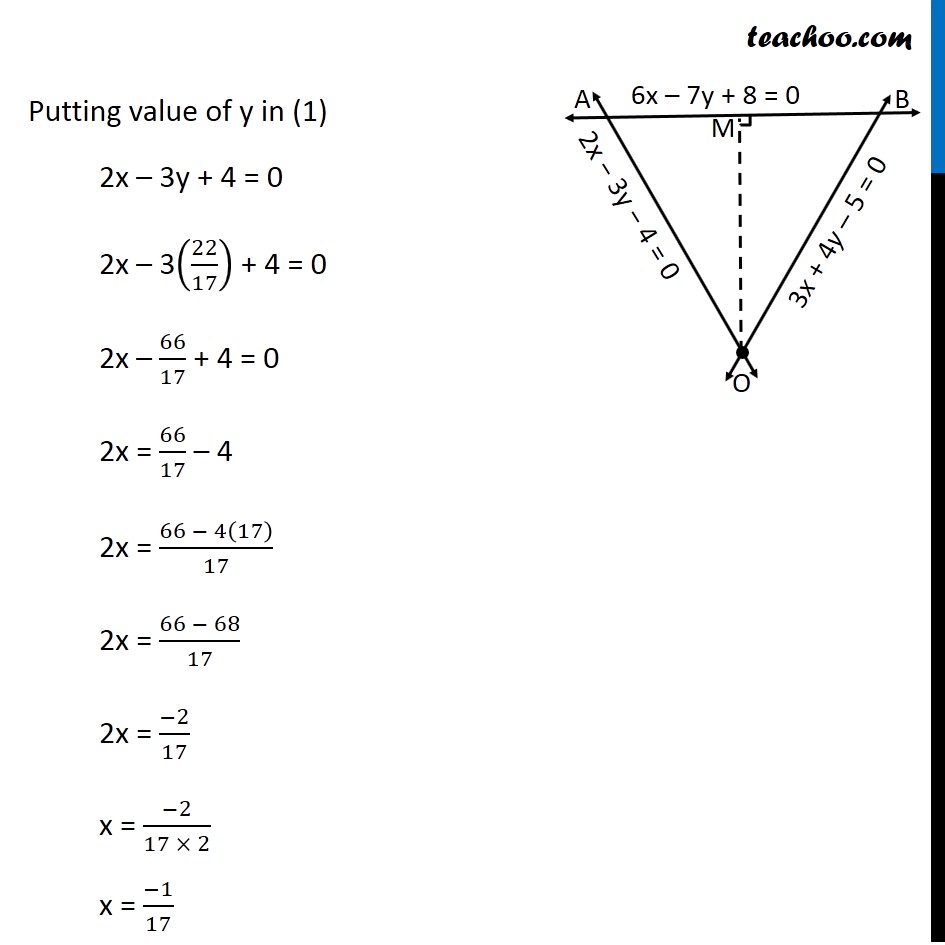
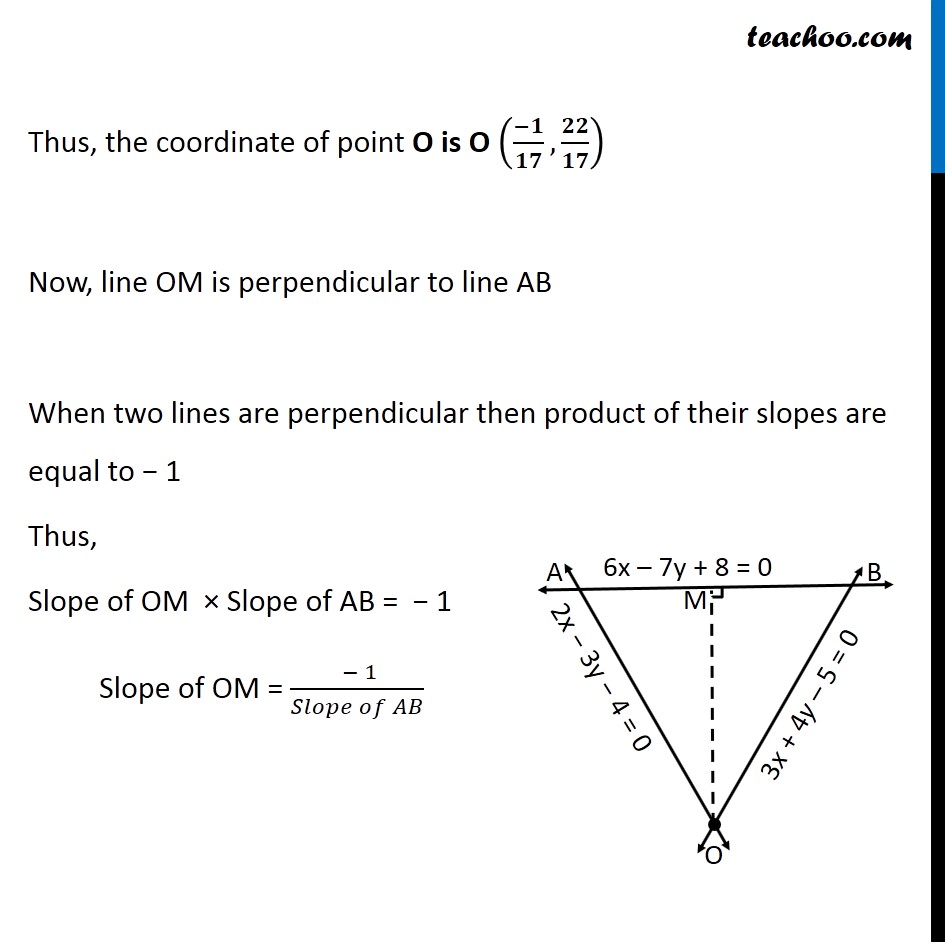
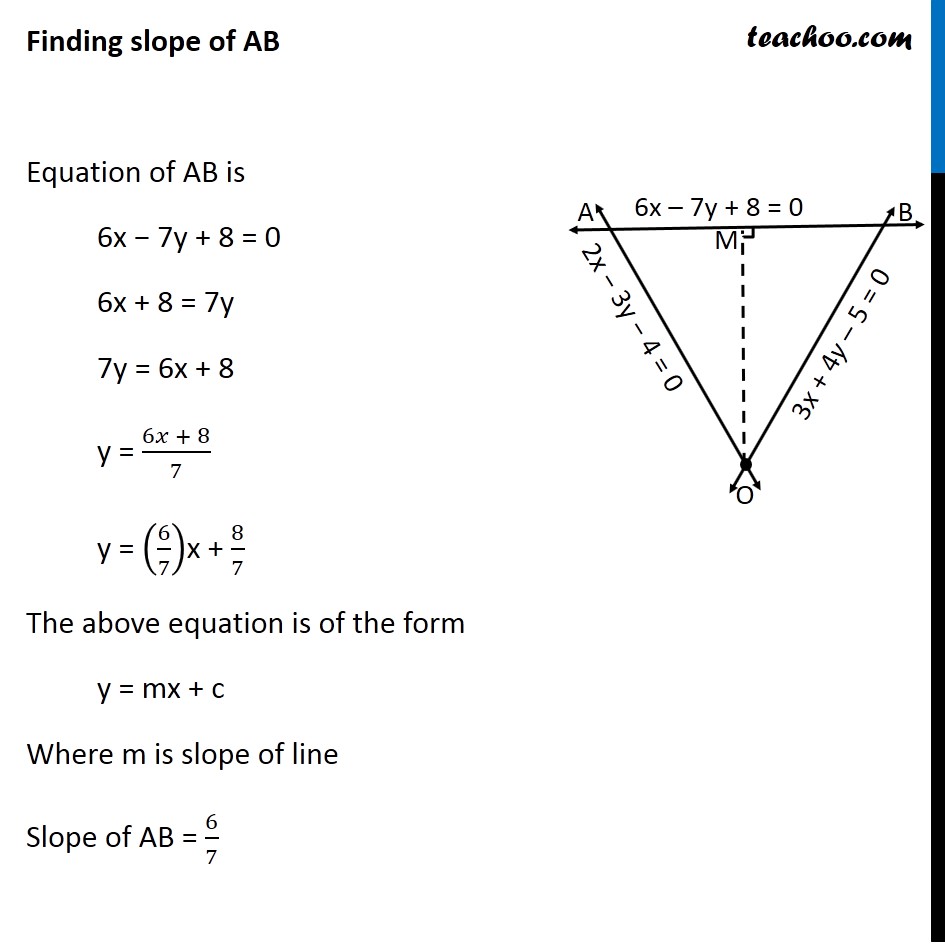
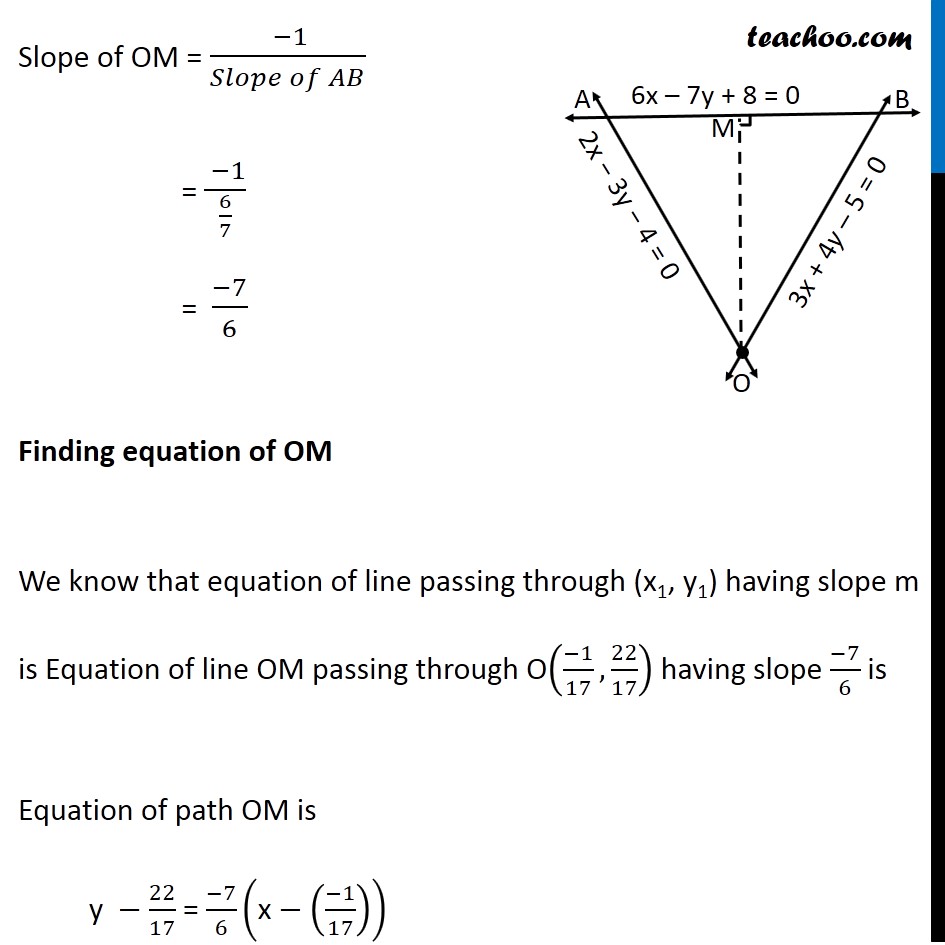
Misc 23 A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow. Let equation of lines OA : 2x − 3y + 4 = 0 OB : 3x + 4y – 5 = 0 AB : 6x – 7y + 8 = 0 The two paths cross at point O ∴ The person is standing at point O From point O, if he has to reach line AB in least time, Least distance from point O to line AB will be perpendicular distance, Let OM ⊥ AB We need to find equation of line OM First we find coordinates of point O Point O is the intersection of OA & OB From (1) 2x – 3y + 4 = 0 2x = 3y – 4 x = (3𝑦 − 4)/2 x = 3/2 y – 4/2 x = 3/2 y – 2 Putting value of x in (2) 3x + 4y – 5 = 0 3(3/2 𝑦−2) + 4y − 5 = 0 9/2y – 6 + 4y − 5 = 0 9/2y + 4y – 11 = 0 (9𝑦 + 8𝑦 )/2 = 11 9y + 8y = 22 17y = 22 y = 22/17 Putting value of y in (1) 2x – 3y + 4 = 0 2x – 3(22/17) + 4 = 0 2x – 66/17 + 4 = 0 2x = 66/17 – 4 2x = (66 − 4(17))/17 2x = (66 − 68)/17 2x = (−2)/17 x = (−2)/(17 × 2) x = (−1)/17 Thus, the coordinate of point O is O ((−𝟏)/𝟏𝟕, 𝟐𝟐/𝟏𝟕) Now, line OM is perpendicular to line AB When two lines are perpendicular then product of their slopes are equal to − 1 Thus, Slope of OM × Slope of AB = − 1 Slope of OM = ( − 1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) Finding slope of AB Equation of AB is 6x − 7y + 8 = 0 6x + 8 = 7y 7y = 6x + 8 y = (6𝑥 + 8)/7 y = (6/7)x + 8/7 The above equation is of the form y = mx + c Where m is slope of line Slope of AB = 6/7 Slope of OM = ( −1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) = ( −1)/(6/7) = (−7)/6 Finding equation of OM We know that equation of line passing through (x1, y1) having slope m is Equation of line OM passing through O((−1)/17, 22/17) having slope (−7)/6 is Equation of path OM is "y "−22/17 = (−7)/6 ("x" −((−1)/17)) "y "−22/17 = (−7)/6 ("x" +1/17) "y "−22/17 = (−7)/6 𝑥−7/6 × 1/17 "y "−22/17 = (−7)/6 𝑥−7/(6 × 17) "y "+ 7/6 x = 22/17 – 7/(6 × 17) (6𝑦 + 7𝑥)/6 = (22(6) − 7)/(6 × 17) (6𝑦 + 7𝑥)/6 = (132 −7)/(6 × 17) (6𝑦 + 7𝑥)/6 = 125/(6 × 17) 6y + 7x = 125/17 17(6y + 7x) = 125 17(6y) + 17(7x) = 125 102y + 119x = 125 Hence the required equation is 119x + 102y = 125