Misc 17 - Chapter 9 Class 11 Straight Lines

Transcript

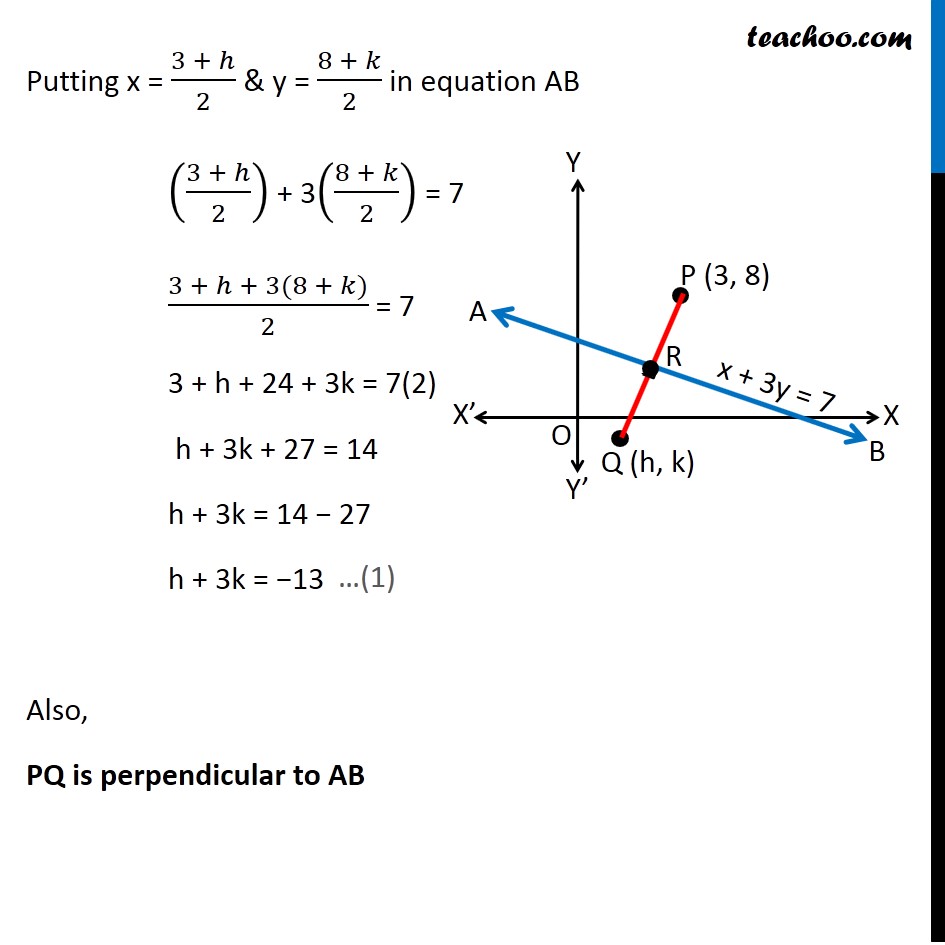
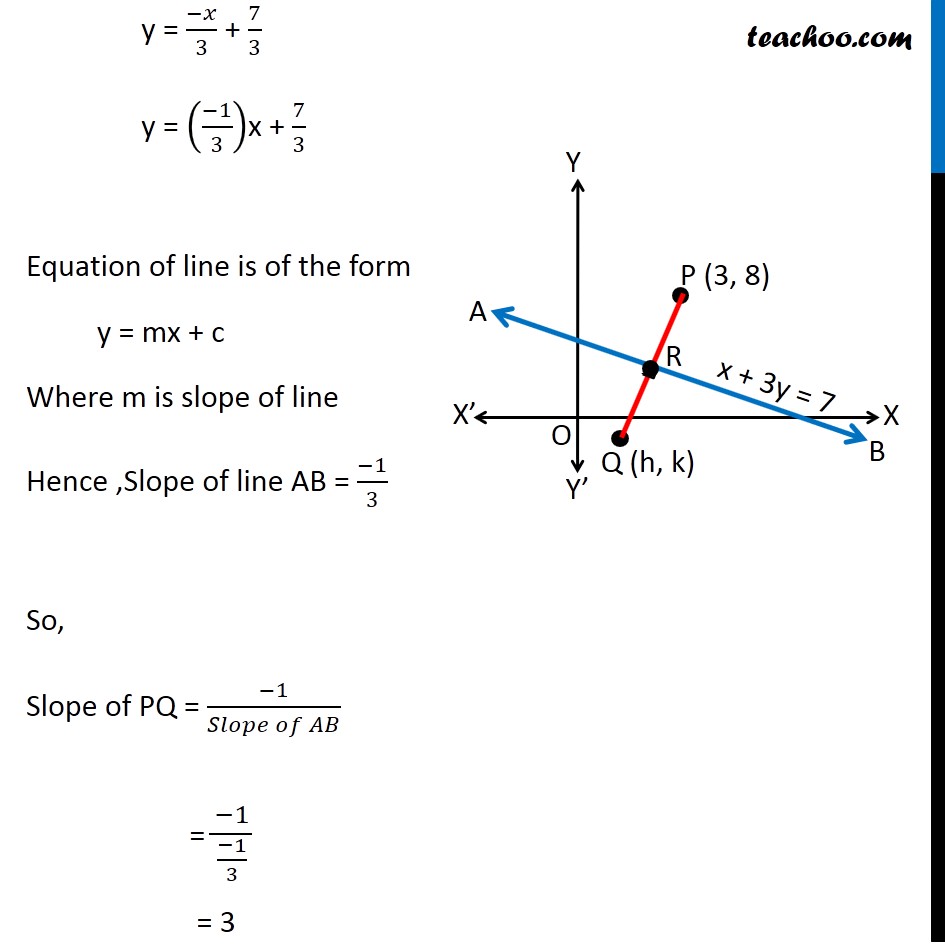
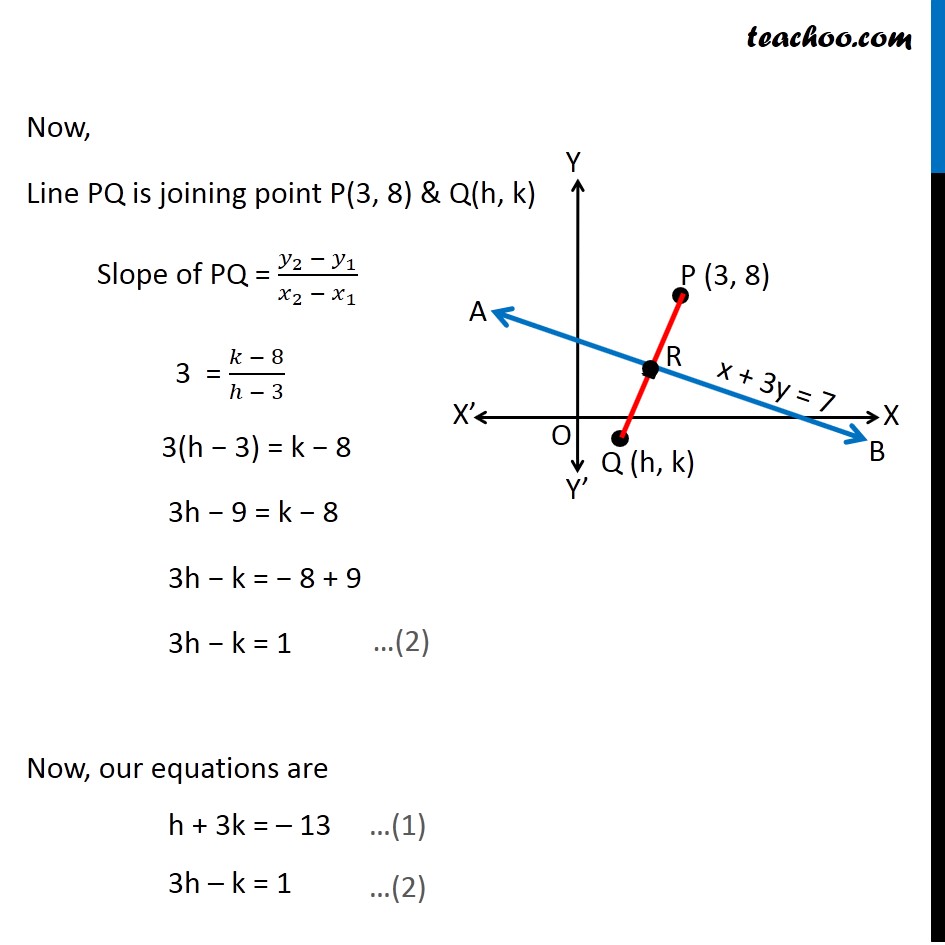
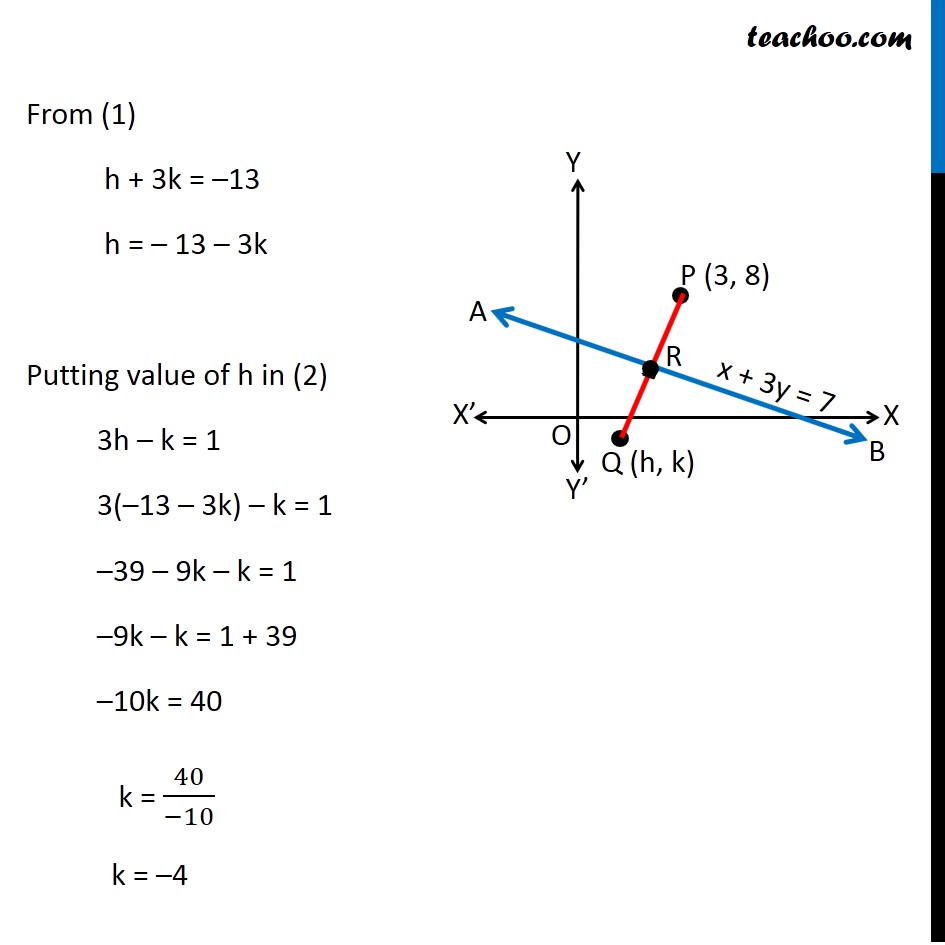
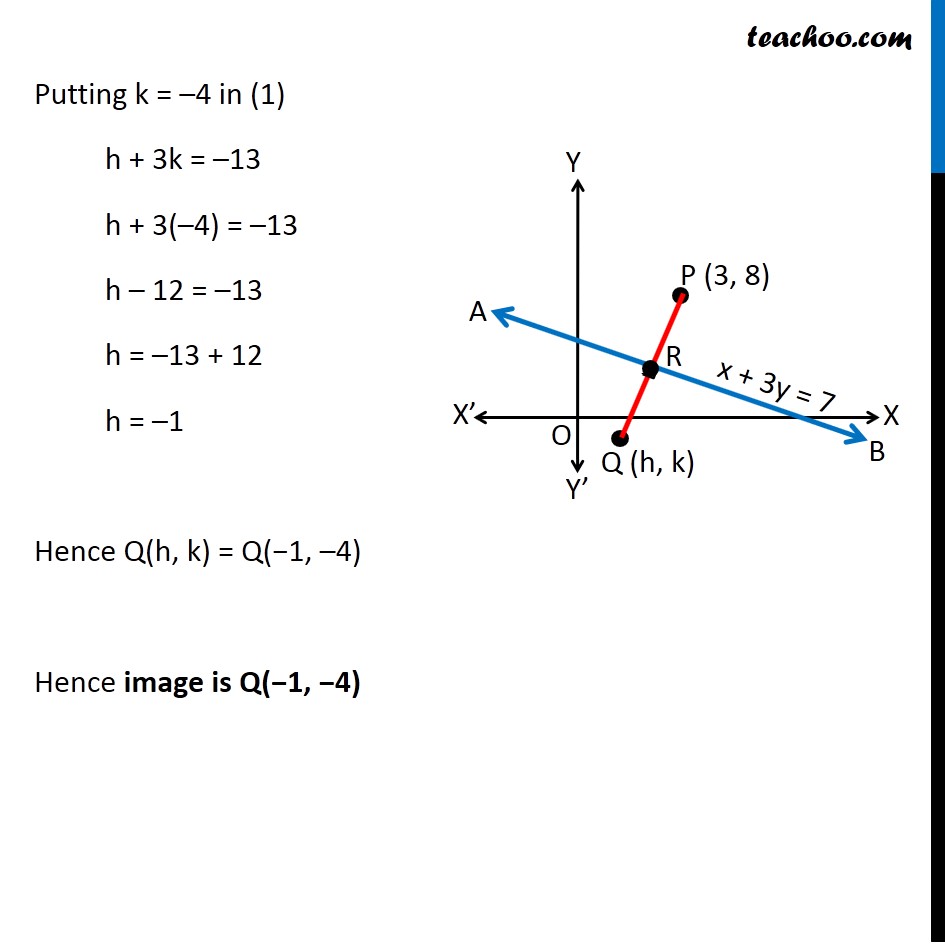
Misc 17 Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror. Let line AB be x + 3y = 7 & point P be (3, 8) Let Q (h, k) be the image of point P (3, 8) in the line AB x + 3y = 7 Since line AB is mirror Point P & Q are at equal distance from line AB, i.e. PR = QR, i.e. R is the mid point of PQ Image is formed perpendicular to mirror i.e. line PQ is perpendicular to line AB Since R is the mid point of PQ We know that Mid point of a line joining (x1, y1) & (x2, y2) = ((𝑥_1+〖 𝑥〗_2)/2, (𝑦_1+ 𝑦_2)/2) Mid point of PQ joining (3, 8) & (h, k) is = ((3 + ℎ)/2 ", " (8 + 𝑘)/2) Coordinate of point R = ((3 + ℎ)/2 ", " (8 + 𝑘)/2) Since point R lies on the line AB It will satisfy the equation of line AB Putting x = (3 + ℎ)/2 & y = (8 + 𝑘)/2 in equation AB ((3 + ℎ)/2) + 3((8 + 𝑘)/2) = 7 (3 + ℎ + 3(8 + 𝑘))/2 = 7 3 + h + 24 + 3k = 7(2) h + 3k + 27 = 14 h + 3k = 14 − 27 h + 3k = −13 Also, PQ is perpendicular to AB We know that If two lines are perpendicular then product of their slope is equal to –1 ∴ Slope of AB × Slope of PQ = –1 Slope of PQ = (−1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) Finding slope of AB Equation of line AB is x + 3y = 7 3y = 7 − x y = (7 − 𝑥)/3 y = 7/3 − 𝑥/3 y = (−𝑥)/3 + 7/3 y = ((−1)/3)x + 7/3 Equation of line is of the form y = mx + c Where m is slope of line Hence ,Slope of line AB = (−1)/3 So, Slope of PQ = (−1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) = (−1)/((−1)/3) = 3 Now, Line PQ is joining point P(3, 8) & Q(h, k) Slope of PQ = (𝑦_2 −〖 𝑦〗_1)/(𝑥_2 − 𝑥_1 ) 3 = (𝑘 − 8)/(ℎ − 3) 3(h − 3) = k − 8 3h − 9 = k − 8 3h − k = − 8 + 9 3h − k = 1 Now, our equations are h + 3k = – 13 3h – k = 1 From (1) h + 3k = –13 h = – 13 – 3k Putting value of h in (2) 3h – k = 1 3(–13 – 3k) – k = 1 –39 – 9k – k = 1 –9k – k = 1 + 39 –10k = 40 k = 40/(−10) k = –4 Putting k = –4 in (1) h + 3k = –13 h + 3(–4) = –13 h – 12 = –13 h = –13 + 12 h = –1 Hence Q(h, k) = Q(−1, –4) Hence image is Q(−1, −4)