Misc 21 - Chapter 9 Class 11 Straight Lines

Transcript

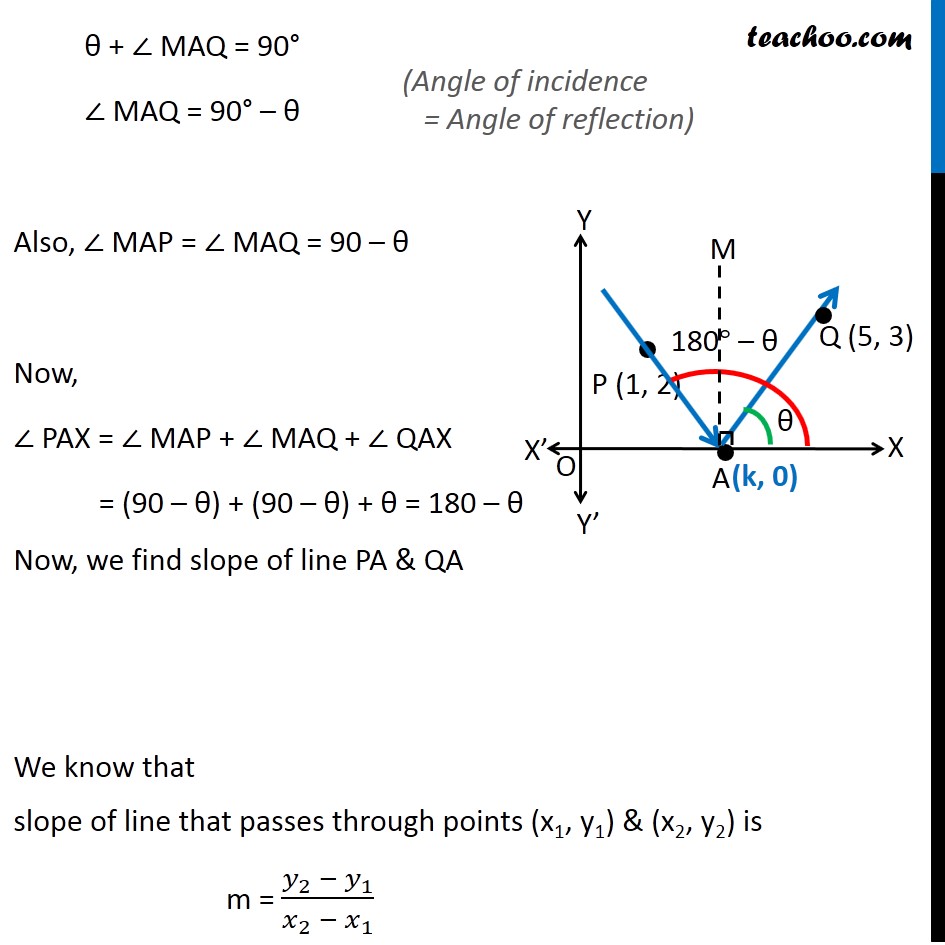
Misc 21 A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A. There is a point A on x-axis on which ray reflects A ray passing through P(1, 2) reflects on point A On reflection, the ray passes through point Q(5, 3) We need to find coordinate of A θ + ∠ MAQ = 90° ∠ MAQ = 90° – θ Also, ∠ MAP = ∠ MAQ = 90 – θ Now, ∠ PAX = ∠ MAP + ∠ MAQ + ∠ QAX = (90 – θ) + (90 – θ) + θ = 180 – θ Now, we find slope of line PA & QA We know that slope of line that passes through points (x1, y1) & (x2, y2) is m = (𝑦_2 − 𝑦_1)/(𝑥_2 − 𝑥_1 ) Line PA Slope of line PA passing through points (1, 2) & (k, 0) is Slope of PA = (0 − 2)/(𝑘 − 1) = ( −2)/(𝑘 − 1) But PA makes angle 180 – θ with positive x-axis Slope of PA = tan (180 – θ) = – tan θ So, – tan θ = ( −2)/(𝑘 − 1) tan θ = ( 2)/(𝑘 − 1) Line QA Slope of line QA passing through points (5, 3) & (k, 0) is Slope of QA = (0 − 3)/(𝑘 − 5) = ( −3)/(𝑘 − 5) But QA makes angle θ with positive x-axis Slope of QA = tan θ So, tan θ = ( −3)/(𝑘 − 5) From (1) & (2) 2/(𝑘 − 1) = ( −3)/(𝑘 − 5) 2(k − 5) = −3(k − 1) 2k − 10 = −3k + 3 2k + 3k = 3 + 10 5k = 13 k = 13/5 Hence point A (𝟏𝟑/𝟓 ", 0" )