



Last updated at Dec. 16, 2024 by Teachoo





Transcript
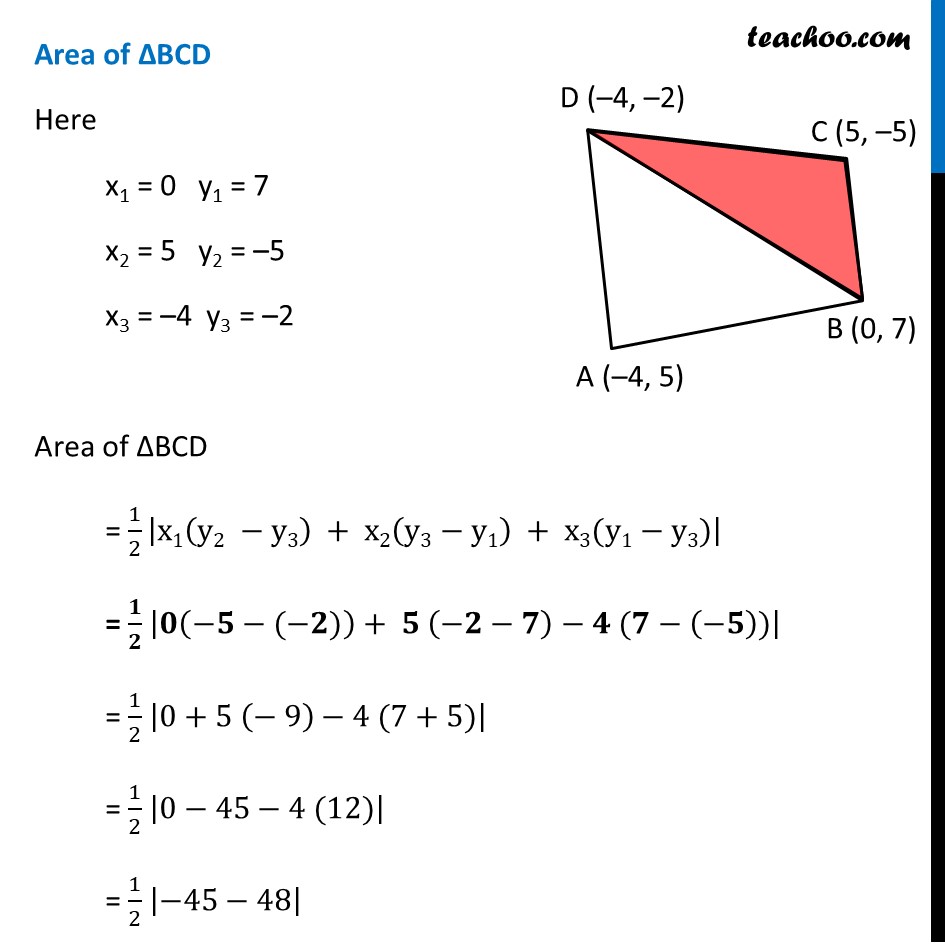
Ex 9.1, 1 Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7), (5, – 5) and (– 4, –2). Also, find its area Let points be A (–4, 5), B (0, 7), C (5, –5), D (–4, –2) Area of quadrilateral ABCD = Area of Δ ABD + Area of ΔBCD Finding Area of Δ ABD & Area of ΔBCD separately Calculating area of ∆ ABD Here x1 = –4, y1 = 5 x2 = 0, y2 = 7 x3 = –4, y3 = –2 Area of ∆ABD = 1/2 |𝑥_1 (𝑦_2−𝑦_3 )+𝑥_2 (𝑦_3−𝑦_1 )+𝑥_3 (𝑦_1−𝑦_3)| = 1/2 |−4(7−(−2))+0(−2−5)+(−4)(5−7)| = 1/2 |−4(7+2)+0−(4)(−2)| = 1/2 |−4(9)+8| = 1/2 |−28| = 1/2 × 28 = 14 Area of ΔBCD Here x1 = 0 y1 = 7 x2 = 5 y2 = –5 x3 = –4 y3 = –2 Area of ΔBCD = 1/2 |x1(y2 −y3) + x2(y3−y1) + x3(y1−y3)| = 1/2 |0(−5−(−2))+ 5 (−2−7)−4 (7−(−5))| = 1/2 |0+5 (− 9)−4 (7+5)| = 1/2 |0−45−4 (12)| = 1/2 |−45−48| = 1/2 | −93| = 93/2 Now, Area of quadrilateral ABCD = Area of Δ ABD + Area of ΔBCD = 14 + 93/2 = (14 × 2 + 93)/2 = (28 + 93)/2 = 121/2 = 60.5 square units Hence area of quadrilateral is 60.5 sq. unit