





Miscellaneous
Misc 2 Important
Misc 3
Misc 4
Misc 5 Important
Misc 6
Misc 7 Important
Misc 8 Important
Misc 9
Misc 10 Important
Misc 11 Important
Misc 12
Misc 13
Misc 14 Important
Misc 15 Important
Misc 16
Misc 17 Important You are here
Misc 18 Important
Misc 19 Important
Misc 20 Important
Misc 21 Important
Misc 22
Misc 23 Important
Question 1 Important Deleted for CBSE Board 2024 Exams
Last updated at April 16, 2024 by Teachoo








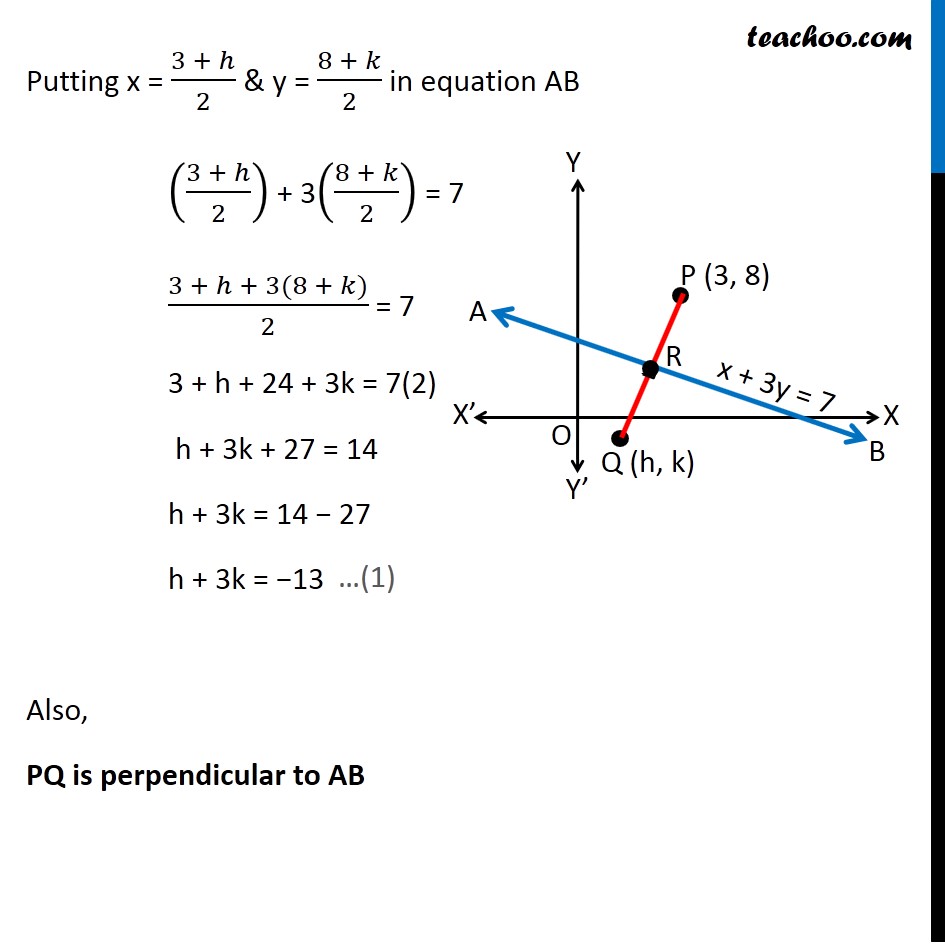
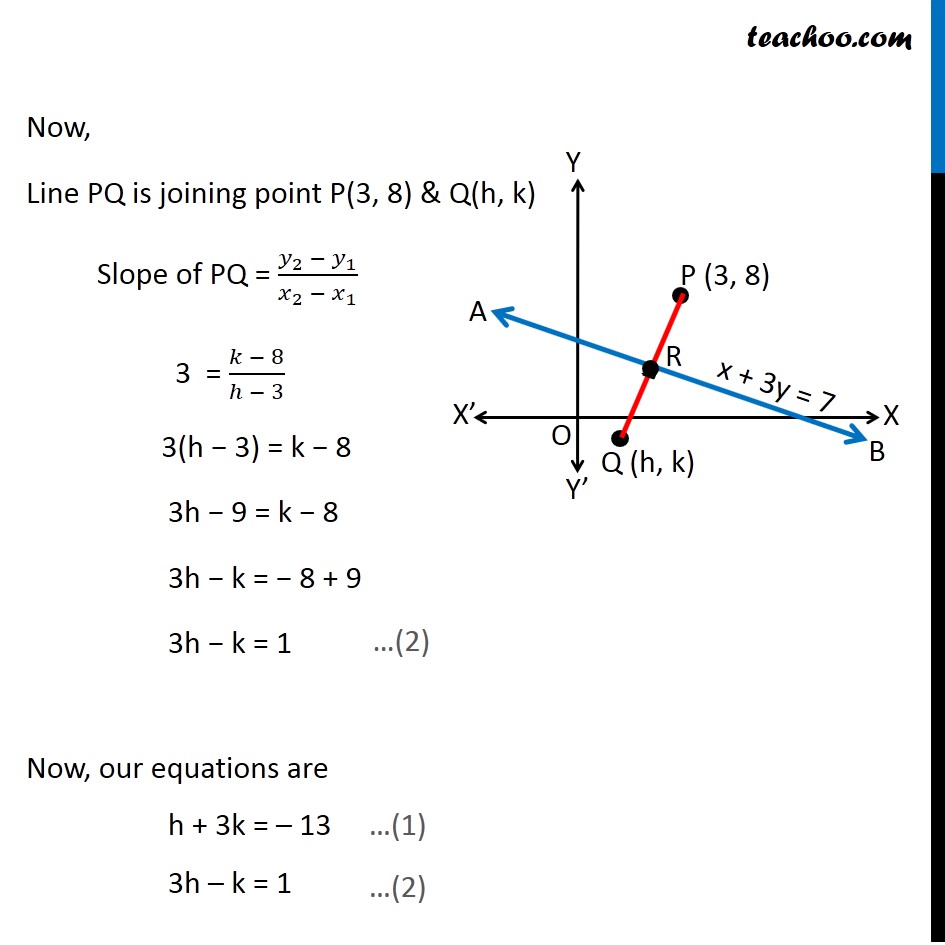
Misc 17 Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror. Let line AB be x + 3y = 7 & point P be (3, 8) Let Q (h, k) be the image of point P (3, 8) in the line AB x + 3y = 7 Since line AB is mirror Point P & Q are at equal distance from line AB, i.e. PR = QR, i.e. R is the mid point of PQ Image is formed perpendicular to mirror i.e. line PQ is perpendicular to line AB Since R is the mid point of PQ We know that Mid point of a line joining (x1, y1) & (x2, y2) = ((𝑥_1+〖 𝑥〗_2)/2, (𝑦_1+ 𝑦_2)/2) Mid point of PQ joining (3, 8) & (h, k) is = ((3 + ℎ)/2 ", " (8 + 𝑘)/2) Coordinate of point R = ((3 + ℎ)/2 ", " (8 + 𝑘)/2) Since point R lies on the line AB It will satisfy the equation of line AB Putting x = (3 + ℎ)/2 & y = (8 + 𝑘)/2 in equation AB ((3 + ℎ)/2) + 3((8 + 𝑘)/2) = 7 (3 + ℎ + 3(8 + 𝑘))/2 = 7 3 + h + 24 + 3k = 7(2) h + 3k + 27 = 14 h + 3k = 14 − 27 h + 3k = −13 Also, PQ is perpendicular to AB We know that If two lines are perpendicular then product of their slope is equal to –1 ∴ Slope of AB × Slope of PQ = –1 Slope of PQ = (−1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) Finding slope of AB Equation of line AB is x + 3y = 7 3y = 7 − x y = (7 − 𝑥)/3 y = 7/3 − 𝑥/3 y = (−𝑥)/3 + 7/3 y = ((−1)/3)x + 7/3 Equation of line is of the form y = mx + c Where m is slope of line Hence ,Slope of line AB = (−1)/3 So, Slope of PQ = (−1)/(𝑆𝑙𝑜𝑝𝑒 𝑜𝑓 𝐴𝐵) = (−1)/((−1)/3) = 3 Now, Line PQ is joining point P(3, 8) & Q(h, k) Slope of PQ = (𝑦_2 −〖 𝑦〗_1)/(𝑥_2 − 𝑥_1 ) 3 = (𝑘 − 8)/(ℎ − 3) 3(h − 3) = k − 8 3h − 9 = k − 8 3h − k = − 8 + 9 3h − k = 1 Now, our equations are h + 3k = – 13 3h – k = 1 From (1) h + 3k = –13 h = – 13 – 3k Putting value of h in (2) 3h – k = 1 3(–13 – 3k) – k = 1 –39 – 9k – k = 1 –9k – k = 1 + 39 –10k = 40 k = 40/(−10) k = –4 Putting k = –4 in (1) h + 3k = –13 h + 3(–4) = –13 h – 12 = –13 h = –13 + 12 h = –1 Hence Q(h, k) = Q(−1, –4) Hence image is Q(−1, −4)