CBSE Class 12 Sample Paper for 2026 Boards
You are here
CBSE Class 12 Sample Paper for 2026 Boards
Last updated at Sept. 2, 2025 by Teachoo
This question is similar to Chapter 8 Class 12 Application of Integrals - Miscellaneous
Please check the question here
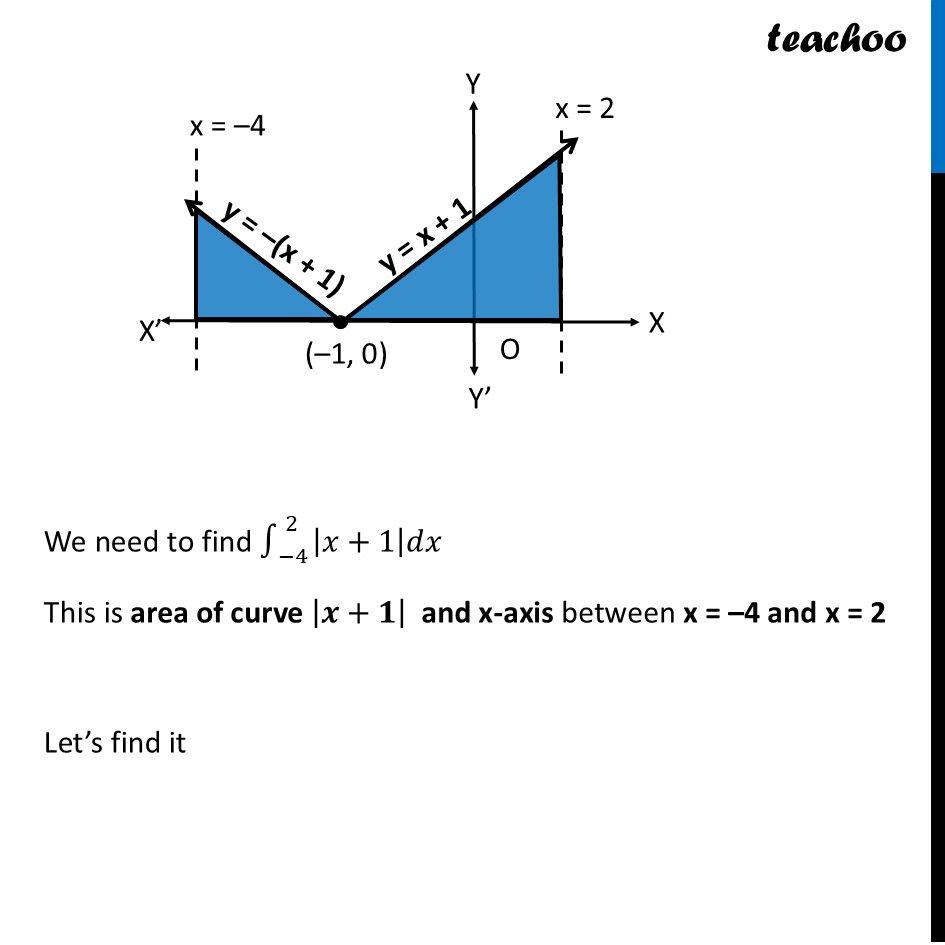
Transcript
Question 28 (A) Sketch the graph π¦=|π₯+1|. Evaluate β«_(β4)^2β|π₯+1|ππ₯. What does the value of this integral represent on the graph? |π₯+1|= {β( (π₯+1) ππ π₯+1β₯0@β(π₯+1) ππ π₯+1<0)β€ = {β((π₯+1) ππ π₯β₯β1@β(π₯+1) ππ π₯<β1)β€ Letβs Draw the graph y = |π+π| We need to find β«_(β4)^2β|π₯+1|ππ₯ This is area of curve |π+π| and x-axis between x = β4 and x = 2 Letβs find it Now, β«_(βπ)^πβγβπ+πβ π πγ =β«_(β4)^(β1)βγβπ₯+1β ππ₯γ+β«_(β1)^2βγβπ₯+1β ππ₯γ =β«_(βπ)^(βπ)βγβ(π+π) π π +β«_(βπ)^πβγ(π+π) π πγγ =[βπ₯^2/2βπ₯]_(β4)^(β1) +[π₯^2/2+π₯]_(β1)^( 2) =[(β(β1)^2)/( 2)β (β1)]β[(β(β4)^2)/( 2)β(β4)] +[2^2/2+ 2]β[(β1)^2/2+ (β1)] =[(β1)/( 2)+1]β[(β16)/( 2)+4]+[2+2]β[1/2β1] =[1/( 2)]β[β8+4]+[4]β[(β1)/2] =[1/( 2)]β[β4]+[4]β[(β1)/2] =1/2+4+4+1/2 =1/2+1/2+8 =1+8 =π
