CBSE Class 12 Sample Paper for 2023 Boards
You are here
CBSE Class 12 Sample Paper for 2023 Boards
Last updated at Dec. 13, 2024 by Teachoo
![[Class 12] Define relation R in set 𝑁 × 𝑁 as follows: For (a, b), (c - CBSE Class 12 Sample Paper for 2023 Boards](https://cdn.teachoo.com/ec1c414c-764c-4db1-980b-df9721356c50/slide15.jpg)
Transcript
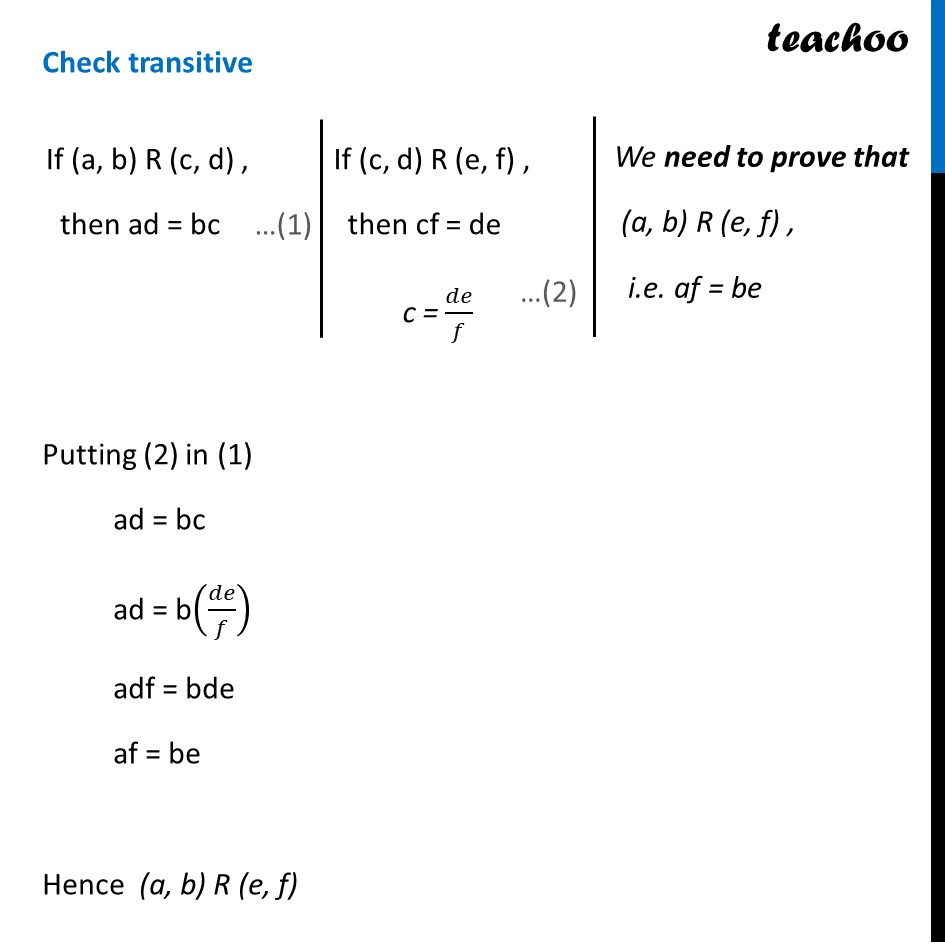
Question 33 (Choice 1) Define the relation R in the set 𝑁 × 𝑁 as follows: For (a, b), (c, d) ∈ 𝑁 × 𝑁, (a, b) R (c, d) iff ad = bc. Prove that R is an equivalence relation in 𝑁 × 𝑁.If (a, b) R (c, d) , then ad = bc Check Reflexive If (a, b) R (a, b), then ab = ba Since, ab = ba Hence , R is reflexive. Check symmetric If (a, b) R (c, d) , then ad = bc Now, If (c, d) R (a, b) , then cb = da Since, ad = bc, da = cb ∴ cb = da So, if (a, b) R (c, d) , then (c, d) R (a, b) So, R is symmetric. Check transitive Putting (2) in (1) ad = bc ad = b(𝑑𝑒/𝑓) adf = bde af = be Hence (a, b) R (e, f) If (a, b) R (c, d) , then ad = bc If (c, d) R (e, f) , then cf = de c = 𝑑𝑒/𝑓 We need to prove that (a, b) R (e, f) , i.e. af = be So, if (a, b) R (c, d) & (c, d) R (e, f) , then (a, b) R (e, f) Thus R is transitive. Thus, R is an equivalence relation.
