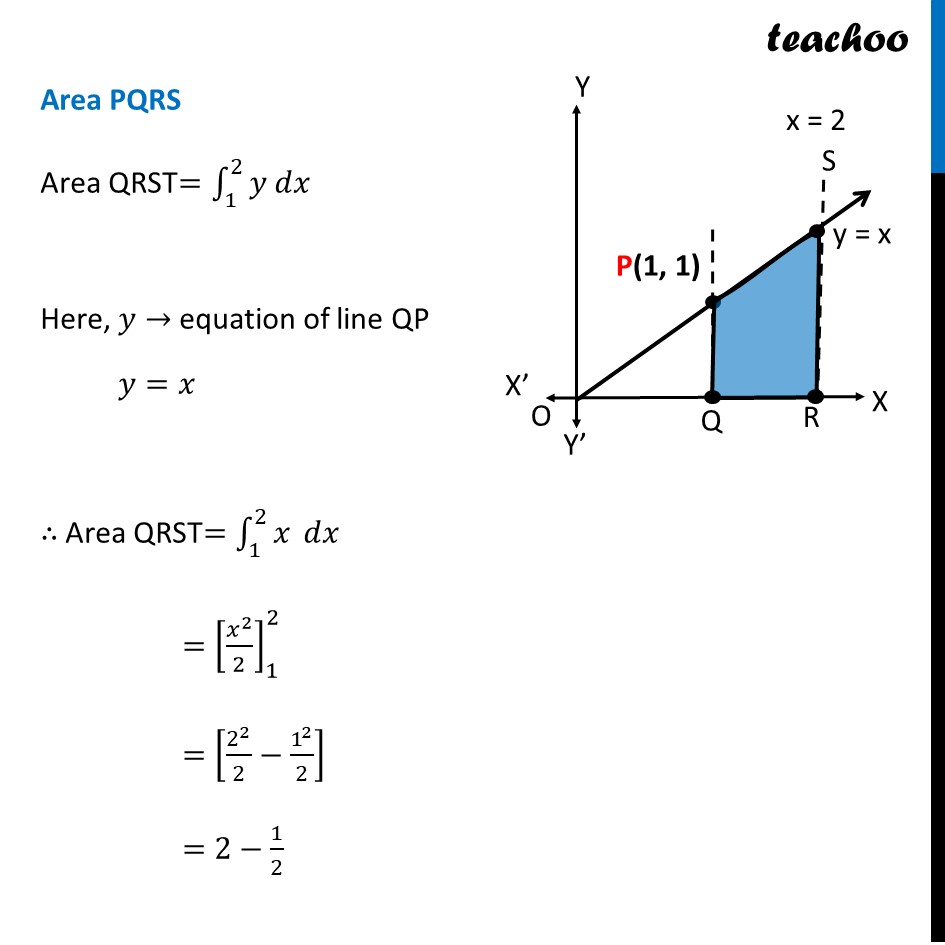
Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ x^2, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integration
![[Class 12] Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥^2 - CBSE Class 12 Sample Paper for 2023 Boards](https://cdn.teachoo.com/137ed61b-144d-44d0-8c2f-14458a820990/slide6.jpg)


CBSE Class 12 Sample Paper for 2023 Boards
CBSE Class 12 Sample Paper for 2023 Boards
Last updated at December 13, 2024 by Teachoo
![[Class 12] Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥^2 - CBSE Class 12 Sample Paper for 2023 Boards](https://cdn.teachoo.com/137ed61b-144d-44d0-8c2f-14458a820990/slide6.jpg)








Transcript
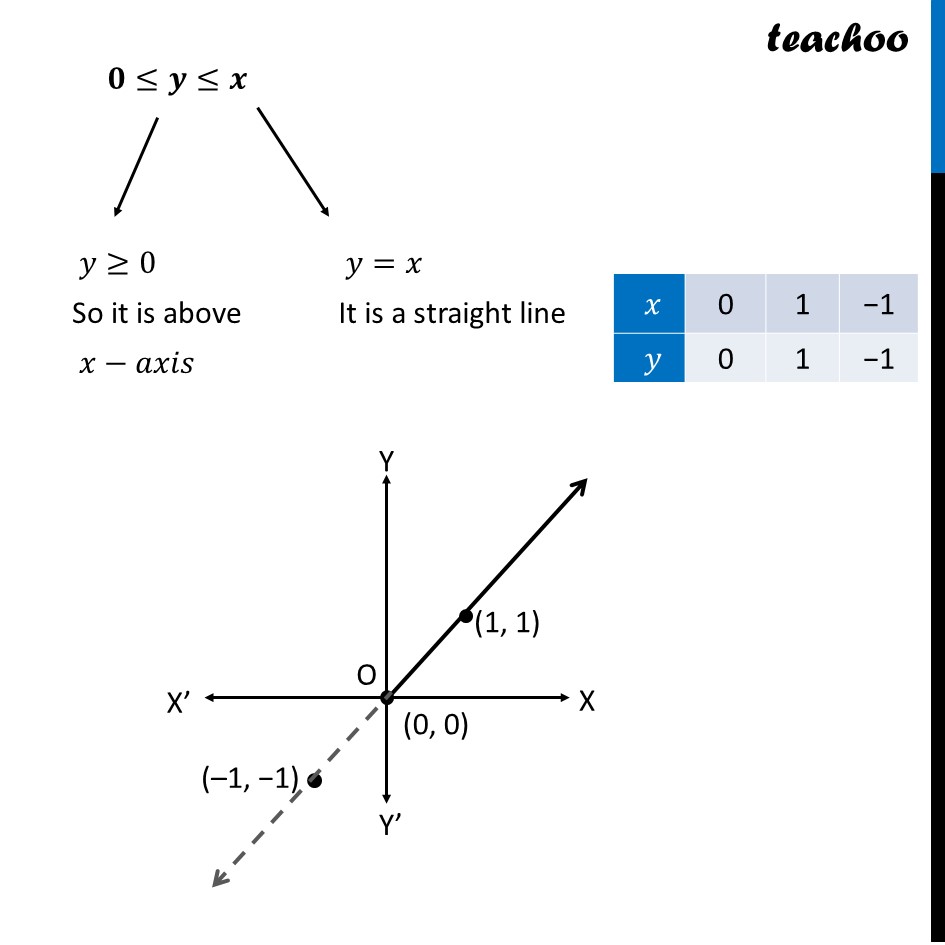
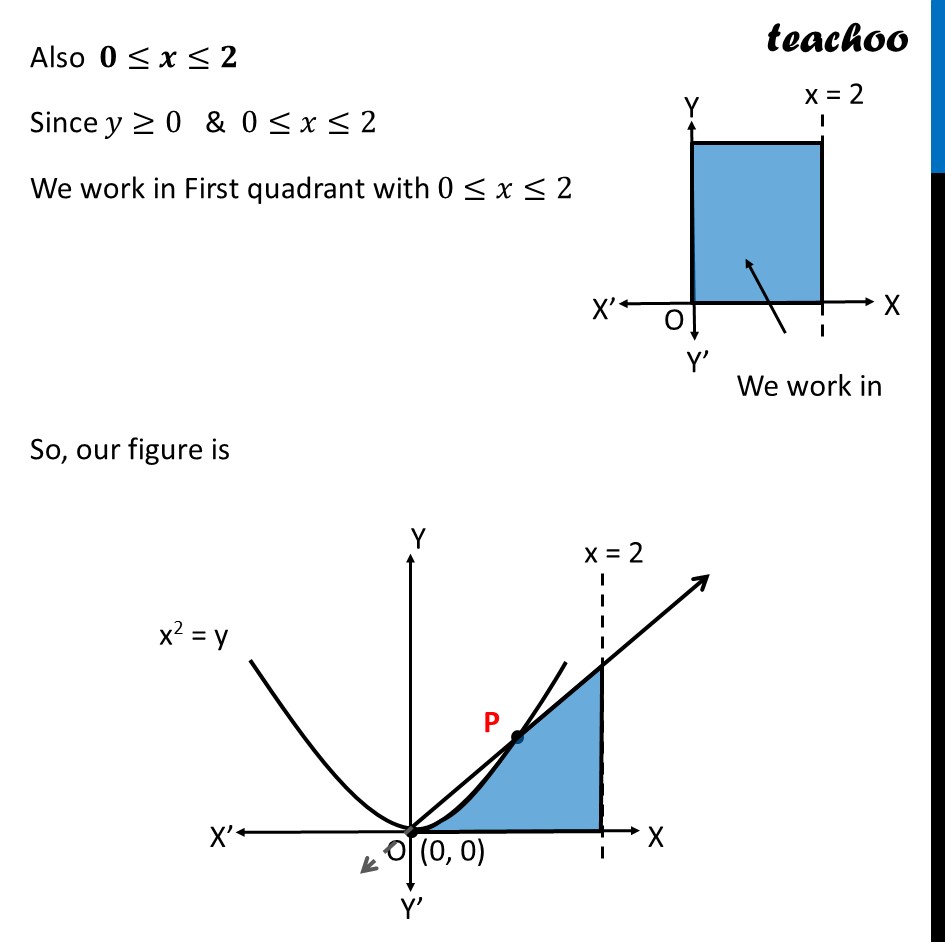
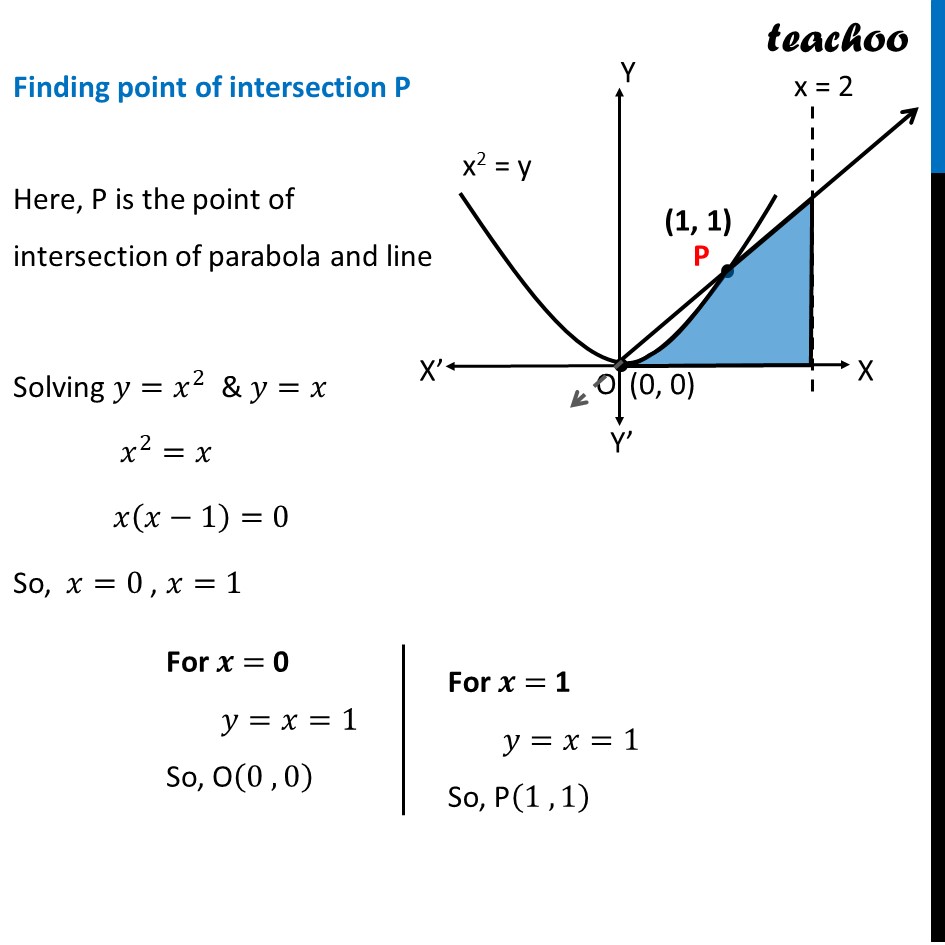
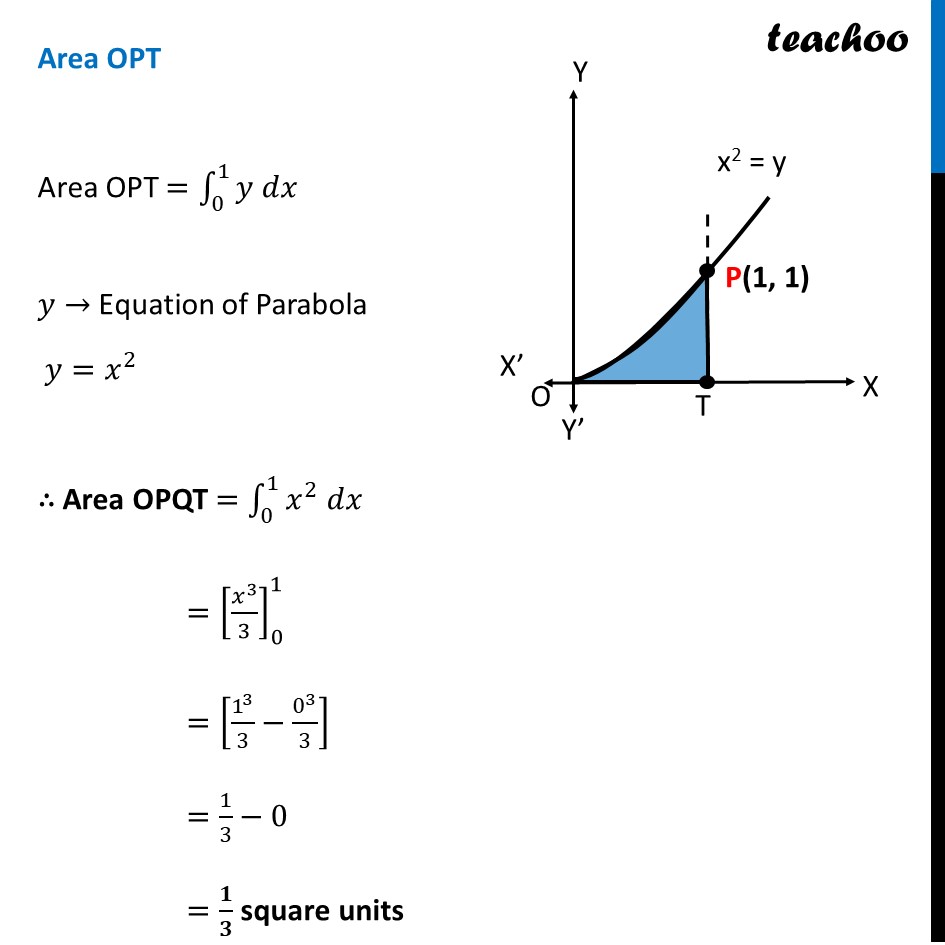
Question 32 Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥^2, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integrationHere, 𝟎≤𝒚≤𝒙^𝟐 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥^2 i.e. 𝑥^2=𝑦 So, it is a parabola 𝟎≤𝒚≤𝒙 𝑦≥0 So it is above 𝑥−𝑎𝑥𝑖𝑠 𝑦=𝑥 It is a straight line Also 𝟎≤𝒙≤𝟐 Since 𝑦≥0 & 0≤𝑥≤2 We work in First quadrant with 0≤𝑥≤2 So, our figure is Finding point of intersection P Here, P is the point of intersection of parabola and line Solving 𝑦=𝑥^2 & 𝑦=𝑥 𝑥^2=𝑥 𝑥(𝑥−1)=0 So, 𝑥=0 , 𝑥=1 For 𝒙 = 0 𝑦=𝑥=1 So, O(0 , 0) For 𝒙 = 1 𝑦=𝑥=1 So, P(1 , 1) Finding area Area required = Area OPQRST Area OPSRQ = Area OPT + Area PQRS Area OPT Area OPT =∫_0^1▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of Parabola 𝑦=𝑥^2 ∴ Area OPQT =∫_0^1▒〖𝑥^2 𝑑𝑥〗 =[𝑥^3/3]_0^1 =[1^3/3−0^3/3] =1/3−0 =𝟏/𝟑 square units Area PQRS Area QRST=∫_1^2▒〖𝑦 𝑑𝑥〗 Here, 𝑦→ equation of line QP 𝑦=𝑥 ∴ Area QRST=∫_1^2▒𝑥 𝑑𝑥 =[𝑥^2/2]_1^2 =[2^2/2−1^2/2] =2−1/2=𝟑/𝟐 square units Thus, Area Required = Area OPQT + Area QPST = 1/3+3/2 = (2 + 9)/6 = 𝟏𝟏/𝟔 square units