NCERT Exemplar - MCQs
You are here
You are here
Last updated at August 14, 2026 by Teachoo
Transcript
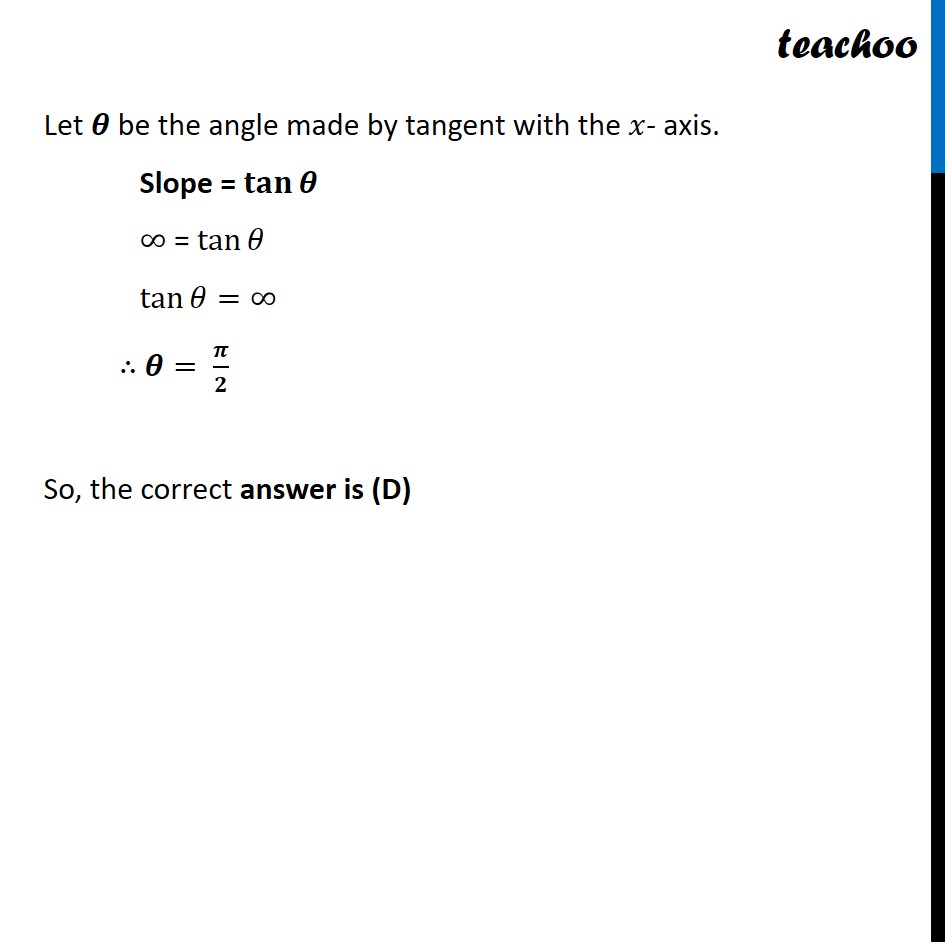
Question 3 The tangent to the curve given by x = et . cost, y = et . sint at t = 𝜋/4 makes with x-axis an angle: 0 (B) 𝜋/4 (C) 𝜋/3 (D) 𝜋/2 Given curve 𝒙=𝒆^𝒕.𝒄𝒐𝒔𝒕 and 𝒚=𝒆^𝒕.𝒔𝒊𝒏𝒕 Finding slope of tangent 𝒅𝒚/𝒅𝒙=(𝒅𝒚/𝒅𝒕)/(𝒅𝒙/𝒅𝒕) 𝒙=𝒆^𝒕.𝒄𝒐𝒔𝒕 Differentiating 𝑥 𝑤.𝑟.𝑡 𝑡 𝑑𝑥/𝑑𝑡=𝑒^𝑡 𝑐𝑜𝑠𝑡−𝑒^𝑡 𝑠𝑖𝑛𝑡 𝒅𝒙/𝒅𝒕=𝑒^𝑡 (𝑐𝑜𝑠𝑡−𝑠𝑖𝑛𝑡) 𝒚=𝒆^𝒕.𝒔𝒊𝒏𝒕 Differentiating y 𝑤.𝑟.𝑡 𝑑𝑦/𝑑𝑡=𝑒^𝑡 𝑠𝑖𝑛𝑡+𝑒^𝑡 𝑐𝑜𝑠𝑡 𝒅𝒚/𝒅𝒕=𝑒^𝑡 (𝑠𝑖𝑛𝑡\+𝑐𝑜𝑠𝑡) Now, 𝒅𝒚/𝒅𝒙=(𝒅𝒚/𝒅𝒕)/(𝒅𝒙/𝒅𝒕) 𝑑𝑦/𝑑𝑥=(𝑒^𝑡 (𝑠𝑖𝑛𝑡\+𝑐𝑜𝑠𝑡)" " )/(𝑒^𝑡 (𝑐𝑜𝑠𝑡−𝑠𝑖𝑛𝑡)" " ) 𝑑𝑦/𝑑𝑥=( (𝒔𝒊𝒏𝒕\+𝒄𝒐𝒔𝒕)" " )/( (𝒄𝒐𝒔𝒕−𝒔𝒊𝒏𝒕)" " ) Putting 𝐭=𝛑/𝟒 ├ 𝒅𝒚/𝒅𝒙┤|_(𝒕=𝝅/𝟒)=( (𝑠𝑖𝑛 𝜋/4 \+ 𝑐𝑜𝑠 𝜋/4)" " )/( (𝑐𝑜𝑠 𝜋/4 − 𝑠𝑖𝑛 𝜋/4)" " ) = (1/√2+1/√2)/(1/√2−1/√2) = (2/(√2))/0 = ∞ Let 𝜽 be the angle made by tangent with the 𝑥- axis. Slope = 𝐭𝐚𝐧𝜽 ∞ = tan𝜃 tan〖𝜃=∞〗 ∴ 𝜽= 𝝅/𝟐 So, the correct answer is (D)
