Misc 12 - Chapter 6 Class 12 Application of Derivatives

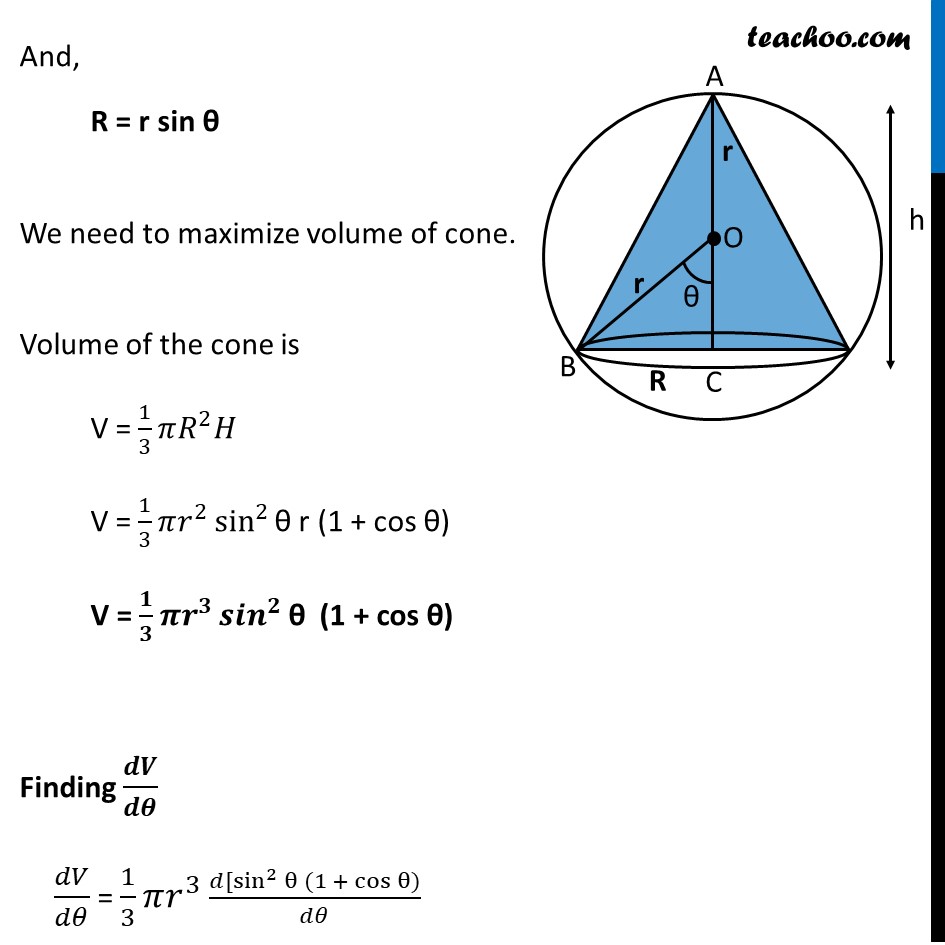
Transcript

Misc 12 Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4𝑟/3 . Given, Radius of sphere = r Let R be the radius of the cone and H be its height. Let ∠ BOC = θ Now, AC = AO + OC H = r + r cos θ H = r (1 + cos θ) And, R = r sin θ We need to maximize volume of cone. Volume of the cone is V = 1/3 𝜋𝑅^2 𝐻 V = 1/3 𝜋𝑟^2 sin^2⁡"θ" r (1 + cos θ) V = 𝟏/𝟑 𝝅𝒓^𝟑 〖𝒔𝒊𝒏〗^𝟐⁡"θ" (1 + cos θ) Finding 𝒅𝑽/𝒅𝜽 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 (𝑑[sin^2⁡〖θ 〗 (1 + cos⁡θ))/𝑑𝜃 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 [2 sin⁡〖"θ" cos⁡〖"θ" (1+cos⁡〖"θ" )+sin^2⁡〖"θ" (−sin⁡〖"θ" )〗 〗 〗 〗 〗 ] 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 (2 sin⁡〖"θ" cos⁡〖"θ" (1+cos⁡〖"θ" )−sin^3⁡"θ" 〗 〗 〗 ) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 (2 sin⁡〖"θ" cos⁡〖"θ" (1+cos⁡〖"θ" )−sin^3⁡"θ" 〗 〗 〗 ) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (2 cos⁡〖"θ" +〖2 cos^2〗⁡〖"θ" −〖𝒔𝒊𝒏〗^𝟐⁡"θ" 〗 〗 ) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (2 cos⁡〖"θ" +〖2 cos^2〗⁡〖"θ" −(𝟏−〖𝒄𝒐𝒔〗^𝟐⁡"θ" 〗 〗)) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (𝟑 〖𝒄𝒐𝒔〗^𝟐⁡〖"θ" +〖𝟐 𝒄𝒐𝒔〗⁡〖"θ" −𝟏〗 〗 ) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (𝟑 〖𝒄𝒐𝒔〗^𝟐⁡〖"θ" +〖𝟑 𝒄𝒐𝒔〗⁡𝜽 〗 −𝒄𝒐𝒔⁡𝜽 −𝟏) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (3 〖𝑐𝑜𝑠 〗⁡"θ" (cos⁡𝜃+1)−1(cos⁡𝜃+1)) 𝑑𝑉/𝑑𝜃 = 1/3 𝜋𝑟^3 sin θ (3 𝑐𝑜𝑠⁡〖"θ" −1〗 )(𝑐𝑜𝑠⁡〖"θ" +1〗 ) Putting 𝒅𝑽/𝒅𝜽 = 0 1/3 𝜋𝑟^3 sin θ (𝑐𝑜𝑠⁡〖"θ" +1〗 ) (3 𝑐𝑜𝑠⁡〖"θ" −1〗 ) = 0 𝐬𝐢𝐧 θ (cos θ + 1) (3 cos "θ" − 1) = 0 𝐜𝐨𝐬 θ + 1 = 0 cos θ = −1 For cone, 0° < θ < 90° & cos θ is negative in 2nd & 3rd quadrant. So cos θ = −1 is not possible 𝟑 𝐜𝐨𝐬 θ − 1 = 0 cos θ = 1/3 θ = cos−1 1/3 cos θ = 𝟏/𝟑 is possible So, 𝒄𝒐𝒔⁡"θ" = 𝟏/𝟑 Thus, H = r (1 + cos θ) H = r ("1 + " 1/3) H = 𝟒𝒓/𝟑 Finding (𝒅^𝟐 𝑽)/(𝒅𝜽^𝟐 ) 𝑑𝑉/𝑑𝜃 = (1/3 𝜋𝑟^3 sin⁡𝜃 (3 cos2 𝜃 + 2 cos⁡𝜃− 1)) = 1/3 𝜋𝑟^3 [cos⁡𝜃 (3 cos^2⁡𝜃+2 cos⁡𝜃−1)+sin⁡𝜃 (6 cos⁡𝜃 (−𝑠𝑖𝑛)−2 sin⁡𝜃 )] = 1/3 𝜋𝑟^3 [3 cos^3⁡𝜃+2 cos^2⁡𝜃−cos⁡𝜃+sin⁡𝜃 (−6 cos⁡𝜃 sin⁡𝜃−2 sin⁡𝜃 )] = 1/3 𝜋𝑟^3 [3 cos^2⁡𝜃+2 cos^2⁡𝜃−cos⁡𝜃−6 sin^2⁡𝜃 cos⁡𝜃−2 sin^2⁡𝜃 ] Now, 𝐜𝐨𝐬⁡𝜽=𝟏/𝟑 And sin2 "θ" = 1 − cos2 "θ" = 1 − (1/3)^2= 1 − 1/9 = 𝟖/𝟗 Putting values in (𝒅^𝟐 𝑽)/(𝒅𝜽^𝟐 ) (𝑑^2 𝑉)/(𝑑𝜃^2 ) = 1/3 𝜋𝑟^3 [3(1/3)^3+2(1/3)^2−1/3−6(1/3)(8/9)−2(8/9)] = 1/3 𝜋𝑟^3 [3(1/27)+2(1/9)−1/3−6(8/27)−2(8/9)] = 1/3 𝜋𝑟^3 [1/9+ 2/9−1/3−16/9−16/9] = 1/3 𝜋𝑟^3 [(−32)/9] = (−𝟑𝟐𝝅𝒓^𝟑)/𝟐𝟕 Thus, (𝑑^2 𝑉)/(𝑑𝜃^2 ) < 0 for 𝐜𝐨𝐬⁡𝜽=𝟏/𝟑 So, V is maximum for 𝐜𝐨𝐬⁡𝜽=𝟏/𝟑 Hence, altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 𝟒𝒓/𝟑 .