Misc 2 - Chapter 6 Class 12 Application of Derivatives

Transcript

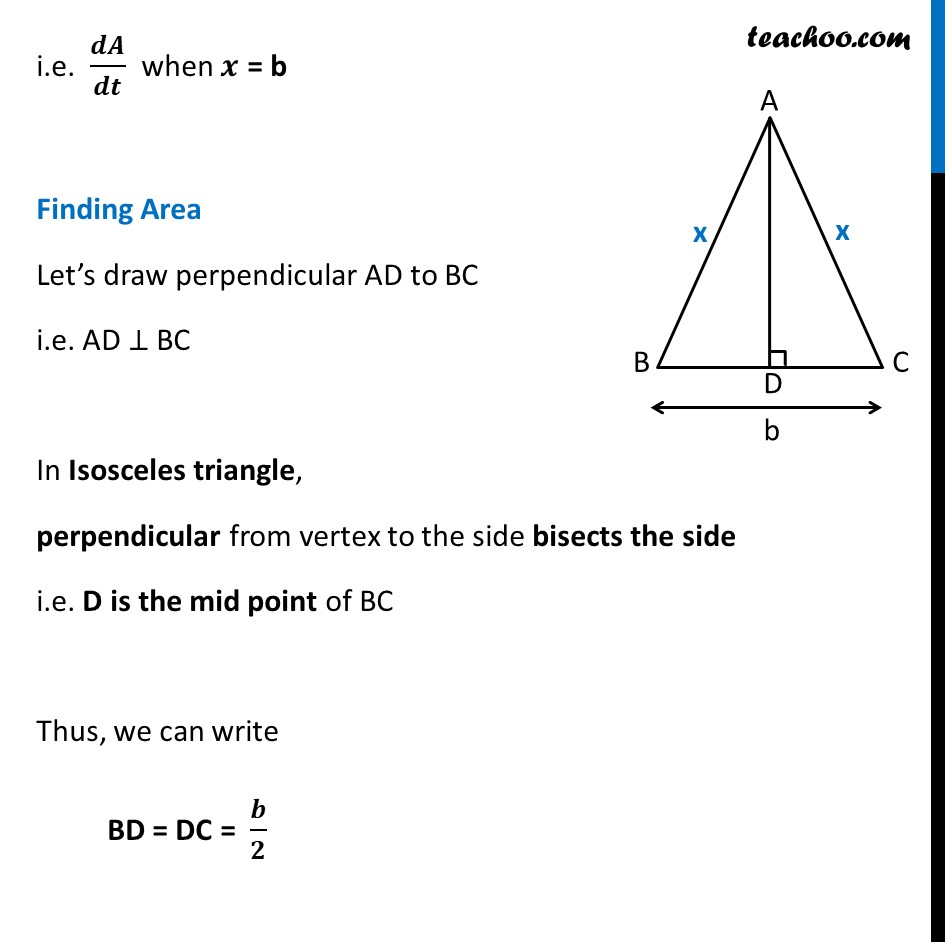
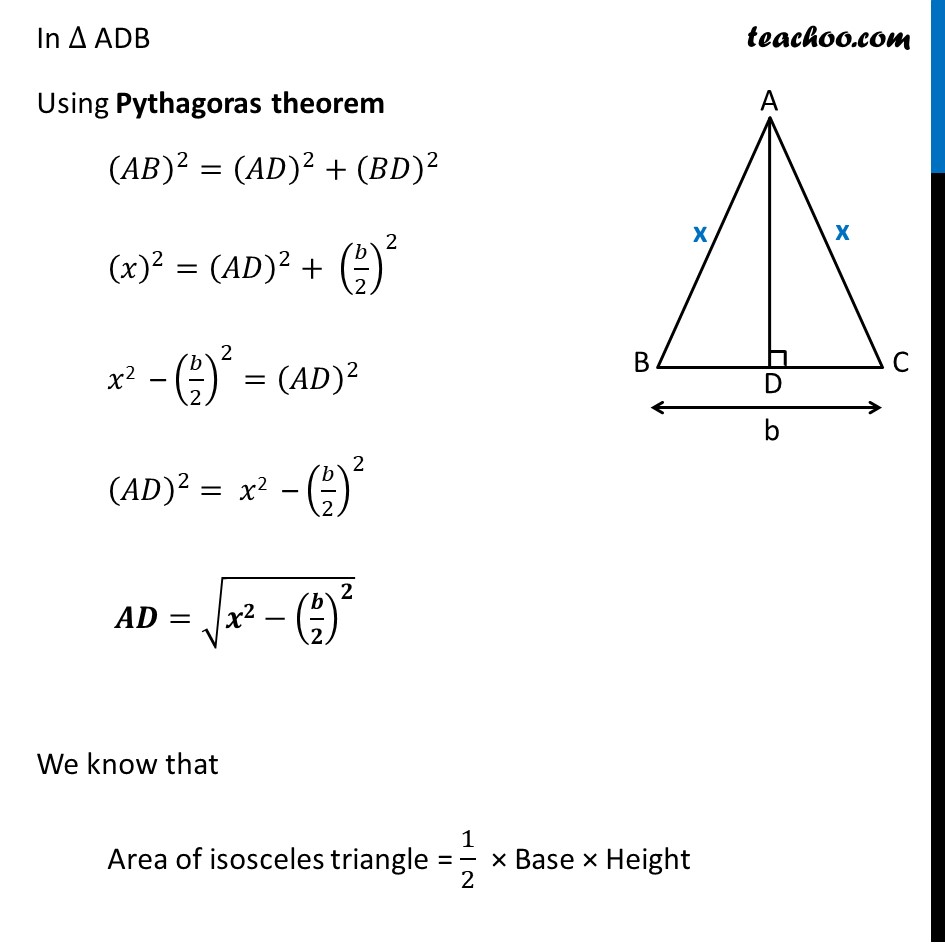
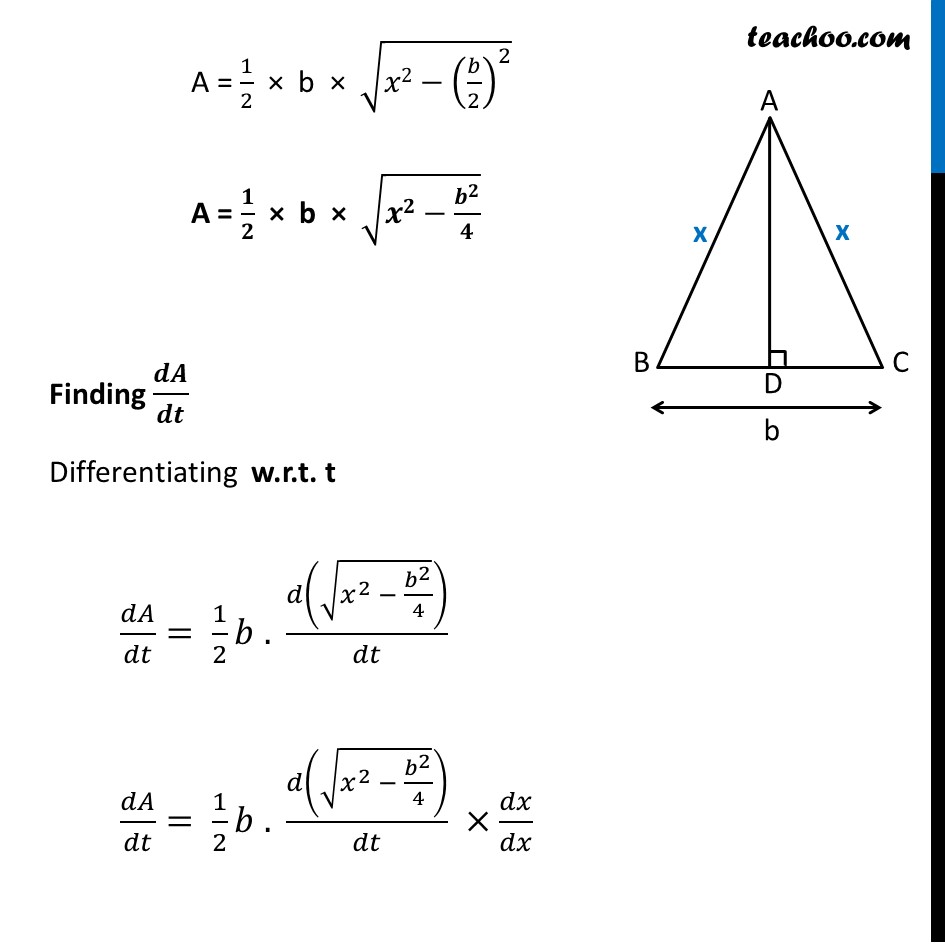
Misc 2 The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base ?Let x be the equal sides of isosceles triangle i.e. AB = AC = 𝒙 And, Base = BC = b Given that equal side of Triangle decreasing at 3 cm per second i.e. 𝑑𝑥/𝑑𝑡= − 3 cm/sec. We need to find how fast is the area decreasing when the two equal sides are equal to the base i.e. 𝒅𝑨/𝒅𝒕 when 𝒙 = b Finding Area Let’s draw perpendicular AD to BC i.e. AD ⊥ BC In Isosceles triangle, perpendicular from vertex to the side bisects the side i.e. D is the mid point of BC Thus, we can write BD = DC = 𝒃/𝟐 In ∆ ADB Using Pythagoras theorem (𝐴𝐵)^2=(𝐴𝐷)^2+(𝐵𝐷)^2 (𝑥)^2=(𝐴𝐷)^2+ (𝑏/2)^2 𝑥2 – (𝑏/2)^2=(𝐴𝐷)^2 (𝐴𝐷)^2 = 𝑥2 – (𝑏/2)^2 𝑨𝑫=√(𝒙𝟐−(𝒃/𝟐)^𝟐 ) We know that Area of isosceles triangle = 1/2 × Base × Height A = 1/2 × b × √(𝑥2−(𝑏/2)^2 ) A = 𝟏/𝟐 × b × √(𝒙𝟐−𝒃^𝟐/𝟒) Finding 𝒅𝑨/𝒅𝒕 Differentiating w.r.t. t 𝑑𝐴/𝑑𝑡= 1/2 𝑏 . 𝑑(√(𝑥^2 − 𝑏^2/4))/𝑑𝑡 𝑑𝐴/𝑑𝑡= 1/2 𝑏 . 𝑑(√(𝑥^2 − 𝑏^2/4))/𝑑𝑡 ×𝑑𝑥/𝑑𝑥 𝑑𝐴/𝑑𝑡= 1/2 𝑏 . 𝑑(√(𝑥^2 − 𝑏^2/4))/𝑑𝑥 ×𝒅𝒙/𝒅𝒕 𝑑𝐴/𝑑𝑡= 1/2 𝑏 . 𝑑(√(𝑥^2 − 𝑏^2/4))/𝑑𝑥 × 𝟑 𝑑𝐴/𝑑𝑡= 1/2 𝑏 [1/(2√(𝑥2 − 𝑏^2/4)) × 𝑑(𝑥^2 − 𝑏^2/4)/𝑑𝑥]× 3" " 𝑑𝐴/𝑑𝑡= 1/2 𝑏 [1/(2√(𝑥2 − 𝑏^2/4)) ×(2𝑥−0)]× 3" " 𝒅𝑨/𝒅𝒕= 𝟑𝒃𝒙/(𝟐√(𝒙𝟐 − 𝒃^𝟐/𝟒)) Finding 𝒅𝑨/𝒅𝒕 at 𝒙 = b ├ 𝑑𝐴/𝑑𝑡┤|_(𝑥 = 𝑏)=(3𝑏^2)/(2√(𝑏^2 − 𝑏^2/4)) = (6𝑏^2)/(4√((4𝑏^2 − 𝑏^2)/4))= (6𝑏^2)/(4√((3𝑏^2)/4))= (6𝑏^2)/((4√3 𝑏)/2)= (6𝑏^2)/(2√3 𝑏)= 3𝑏/√3 =𝑏√3 Since dimension of area is cm2 and time is seconds ∴ 𝑑𝐴/𝑑𝑡 = 𝒃√𝟑 cm2/s