







Miscellaneous
Last updated at April 16, 2024 by Teachoo









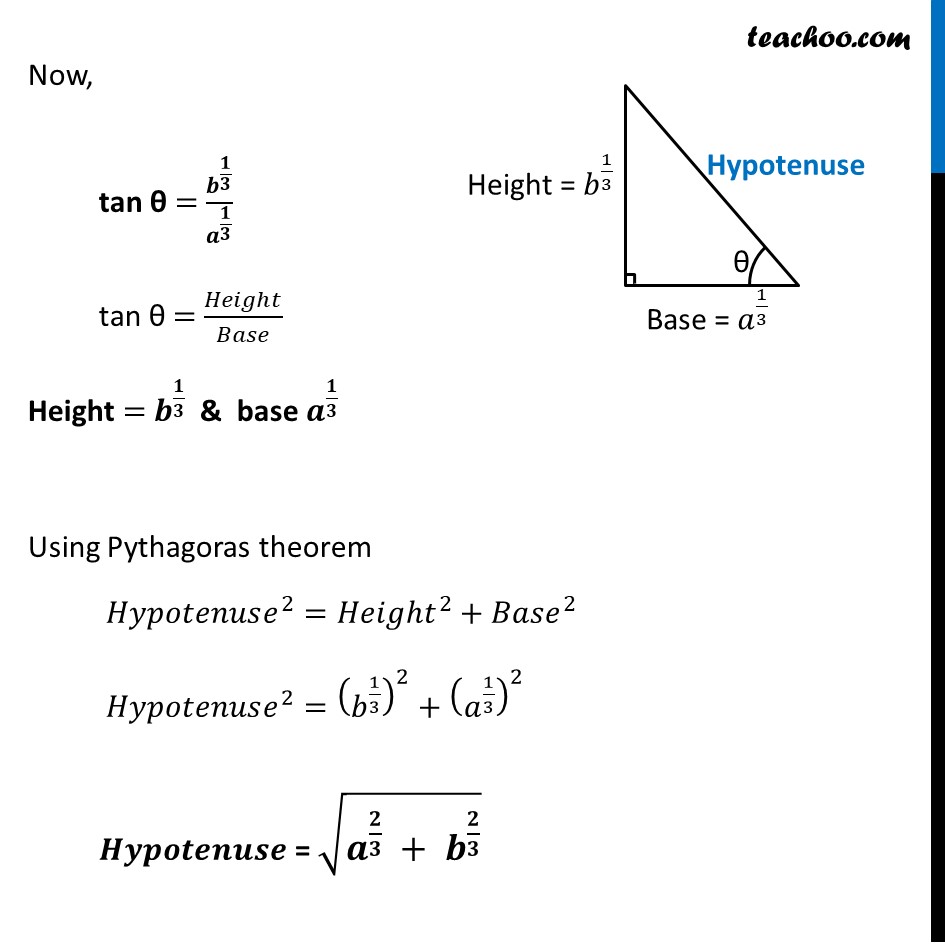
Misc 9 A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is 〖〖(𝑎〗^(2/3) + 𝑏^(2/3)) 〗^(3/2)Let P be the point on the hypotenuse AC Given point P is at distance a & b from sides of triangle Let’s construct PL ⊥ AB & PM ⊥ BC ∴ PL = a & PM = b Let ∠ ACB = θ Thus, ∠ APL = θ We need to find maximum length of the hypotenuse Let l be the length of the hypotenuse , ∴ l = AP + PC In ∆ 𝑨𝑷𝑳 cos θ = (𝑆𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝜃 )/(𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 ) cos θ = 𝑃𝐿/𝐴𝑃 cos θ = 𝑎/𝐴𝑃 AP = 𝑎/cos𝜃 AP = 𝒂 𝒔𝒆𝒄𝜽 In ∆ 𝑷𝑴𝑪 sin θ = (𝑆𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝜃)/(𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 ) sin θ = 𝑃𝑀/𝑃𝐶 sin θ = (𝑏 )/𝑃𝐶 PC = 𝑏/sin𝜃 PC = 𝒃 𝒄𝒐𝒔𝒆𝒄 𝜽 Now, l = AP + PC l = a sec θ + b cosec θ Differentiating w.r.t θ 𝒅𝒍/𝒅𝜽=𝑑(𝑎 sec〖𝜃 + 𝑏 𝑐𝑜𝑠𝑒𝑐 𝜃〗 )/𝑑𝜃 𝑑𝑙/𝑑𝜃= a sec θ tan θ – b cosec θ cot θ Putting 𝒅𝒍/𝒅𝜽=𝟎 a sec θ tan θ – b cosec θ cot θ = 0 a 1/cos𝜃 . sin𝜃/〖 cos〗𝜃 −𝑏 . 1/sin〖𝜃 〗 × cos𝜃/sin𝜃 =0 (𝑎 sin𝜃)/cos^2𝜃 −(𝑏 cos𝜃)/sin^2𝜃 =0 (𝑎 sin𝜃)/cos^2𝜃 = (𝑏 cos𝜃)/sin^2𝜃 a sin θ × sin2 θ = b cos θ cos2 θ a sin3 θ = b cos3 θ sin^3𝜃/cos^3𝜃 = 𝑏/𝑎 tan3 θ = 𝑏/𝑎 tan θ = (𝒃/𝒂)^(𝟏/𝟑) Finding (𝒅^𝟐 𝒍)/(𝒅^𝟐 𝜽) 𝑑𝑙/𝑑𝜃=𝑎 sec〖θ tan𝜃−𝑏 𝑐𝑜𝑠𝑒𝑐 𝜃 cot𝜃 〗 Differentiating w.rt θ (𝑑^2 𝑙)/(𝑑^2 𝜃)= 𝑑(𝑎 sec〖𝜃 tan〖𝜃 − 𝑏 𝑐𝑜𝑠𝑒𝑐𝜃 cot𝜃 〗 〗 )/𝑑𝜃 = a 𝑑(sec〖𝜃 tan𝜃 〗 )/𝑑𝜃−𝑏 𝑑(𝑐𝑜𝑠𝑒𝑐 𝜃 cot𝜃 )/𝑑𝜃 = a((sec𝜃 )^′ tan𝜃+(tan𝜃 )^′ sec𝜃 )−𝑏((𝑐𝑜𝑠𝑒𝑐 𝜃)^′ cot𝜃+(cot𝜃 )^′ 𝑐𝑜𝑠𝑒𝑐 𝜃) = a (sec𝜃.tan〖𝜃.tan𝜃+sec^2〖𝜃.sec𝜃 〗 〗 )−𝑏((−𝑐𝑜𝑠𝑒𝑐 𝜃.cot𝜃 ) cot𝜃+(−𝑐𝑜𝑠𝑒𝑐^2 𝜃).𝑐𝑜𝑠𝑒𝑐 𝜃) = a(sec〖𝜃 tan^2〖𝜃+sec^3𝜃 〗 〗 )−𝑏(−𝑐𝑜𝑠𝑒𝑐 𝜃 cot^2〖𝜃−𝑐𝑜𝑠𝑒𝑐^3 𝜃〗 ) = a sec θ (〖𝒕𝒂𝒏〗^𝟐〖𝜽+〖𝒔𝒆𝒄〗^𝟐𝜽 〗 )+𝑏 𝑐𝑜𝑠𝑒𝑐 𝜃(〖〖𝒄𝒐𝒕〗^𝟐 𝜽〗〖+𝒄𝒐𝒔𝒆𝒄^𝟐 𝜽〗 ) Here, square terms – (〖𝒕𝒂𝒏〗^𝟐〖𝜽+〖𝒔𝒆𝒄〗^𝟐𝜽 〗 ) (〖〖𝒄𝒐𝒕〗^𝟐 𝜽〗〖+𝒄𝒐𝒔𝒆𝒄^𝟐 𝜽〗 ) are always positive And Since θ is acute, i.e. 0 < θ < 𝜋/2 ∴ θ lies in 1st quadrant So, sec θ & cosec θ will be positive Thus, (𝒅^𝟐 𝒍)/(𝒅^𝟐 𝜽) > 0 at tan θ = (𝑏/𝑎)^(1/3) ∴ l is least when tan θ = (𝑏/𝑎)^(1/3) Now, tan θ = 𝒃^(𝟏/𝟑)/𝒂^(𝟏/𝟑) tan θ = 𝐻𝑒𝑖𝑔ℎ𝑡/𝐵𝑎𝑠𝑒 Height = 𝒃^(𝟏/𝟑) & base 𝒂^(𝟏/𝟑) Using Pythagoras theorem 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒^2=𝐻𝑒𝑖𝑔ℎ𝑡^2+𝐵𝑎𝑠𝑒^2 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒^2=(𝑏^(1/3) )^2+(𝑎^(1/3) )^2 𝑯𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆 = √(𝒂^(𝟐/𝟑) + 𝒃^(𝟐/𝟑) ) Least value of l Least value of l = a sec θ + b cosec θ = a × (𝑯𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆 )/(𝑩𝒂𝒔𝒆 )+𝒃 "× " (𝑯𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆 )/(𝑯𝒆𝒊𝒈𝒉𝒕 ) = a × √(𝑎^(2/3) + 𝑏^(2/3) )/𝑎^(1/3) +b ×√(𝑎^(2/3) + 𝑏^(2/3) )/𝑏^(1/3) l = √(𝑎^(2/3)+𝑏^(2/3) ) (𝑎^(1 − 1/3)+𝑏^(1 − 1/3) ) l = √(𝑎^(2/3)+𝑏^(2/3) ) (𝑎^(2/3)+𝑏^(2/3) ) l = (𝑎^(2/3)+𝑏^(2/3) )^(1/2 + 1) l = (𝒂^(𝟐/𝟑)+𝒃^(𝟐/𝟑) )^(𝟑/𝟐) Hence l = (𝒂^(𝟐/𝟑)+𝒃^(𝟐/𝟑) )^(𝟑/𝟐) Hence proved..