Question 7 - Examples - Chapter 9 Class 11 Straight Lines

Transcript

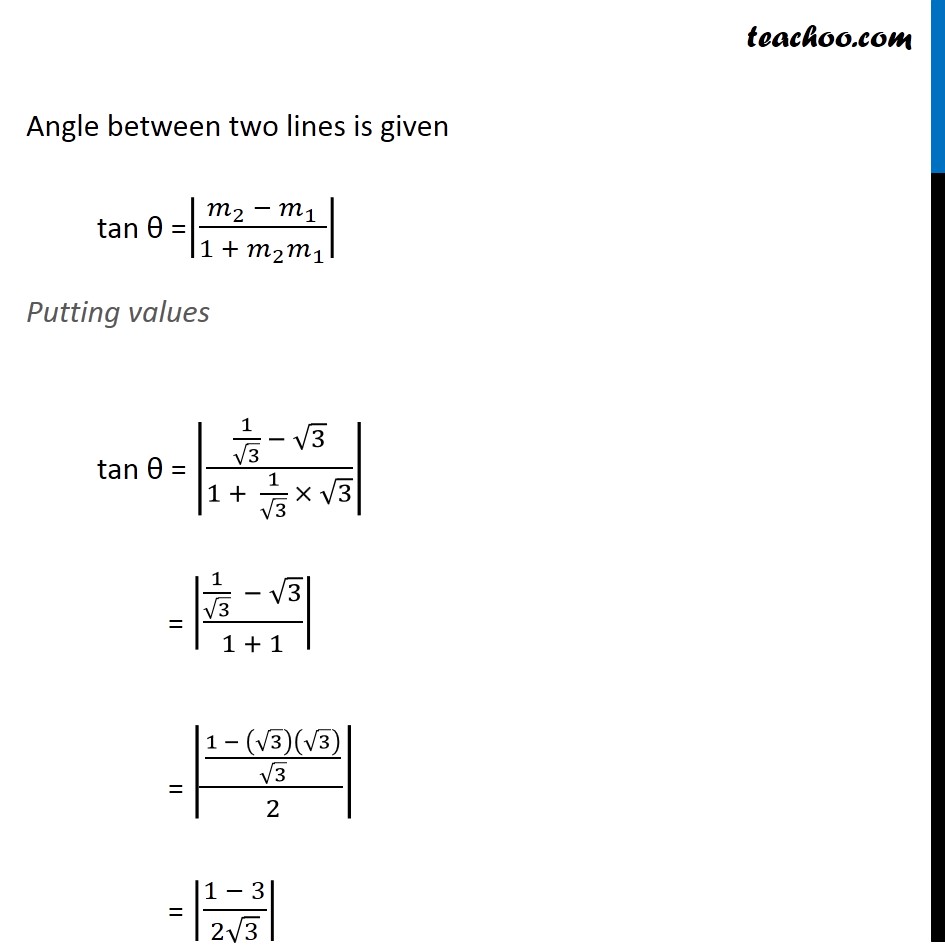
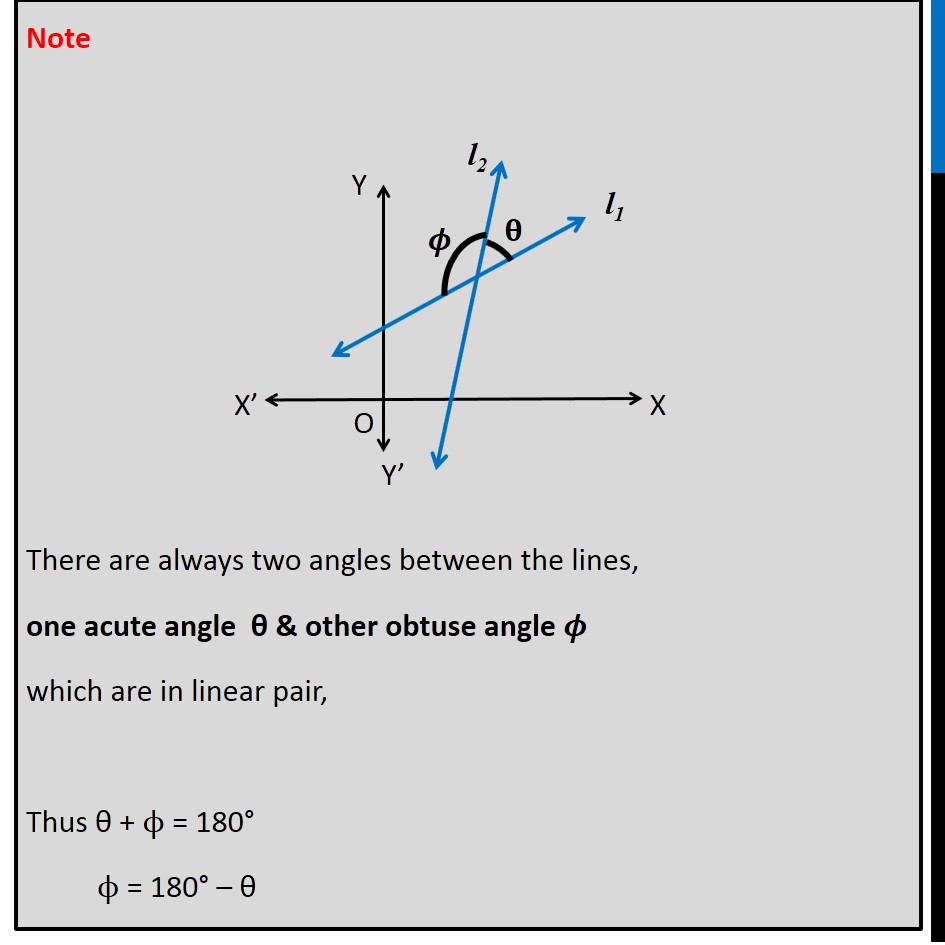
Question 7 Find the angle between the lines y − √3x − 5 = 0 and √3y − x + 6 = 0 . Let the lines be y − √3 x − 5 = 0 √3 y − x + 6 = 0 We know that angle between 2 lines (θ) can be found by using formula tan θ =|(𝑚_2 − 𝑚_1)/(1 + 𝑚_2 𝑚_1 )| Let the slope of line (1) be m1 & slope of line (2) be m2 Calculating m1 From (1) y – √3x – 5 = 0 y = √3x + 5 The above equation is of the form y = mx + c where m is the slope Thus, m1 = √𝟑 Calculating m1 From (2) √3 y – x + 6 = 0 √3 y = x − 6 y = (𝑥 − 6)/√3 y = 1/√3x − 6/√3 The above equation is of the form y = mx + c where m is the slope Thus, m2 = 𝟏/√𝟑 Angle between two lines is given tan θ =|(𝑚_2 − 𝑚_1)/(1 + 𝑚_2 𝑚_1 )| Putting values tan θ = |(1/√3 − √3)/(1 + 1/√3 × √3)| = |(1/√3 − √3)/(1 + 1)| = |((1 − (√3)(√3))/√3)/2| = |(1 − 3)/(2√3)| = |( −2)/(2√3)| = |( −1)/√3| = 1/√3 Thus, tan θ = 1/√3 We know that tan 30° = 1/√3 So, tan θ = tan 30° θ = 30° Thus, the acute angle between the lines (1) & (2) is θ = 30° & obtuse angle between (say ϕ) these two lines is ϕ = 180 − θ ϕ = 180 − 30° ϕ = 150° Thus, the required angle between lines is 30° or 150° Note There are always two angles between the lines, one acute angle θ & other obtuse angle 𝝓 which are in linear pair, Thus θ + ϕ = 180° ϕ = 180° – θ