Question 28 (B) - CBSE Class 12 Sample Paper for 2026 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Transcript

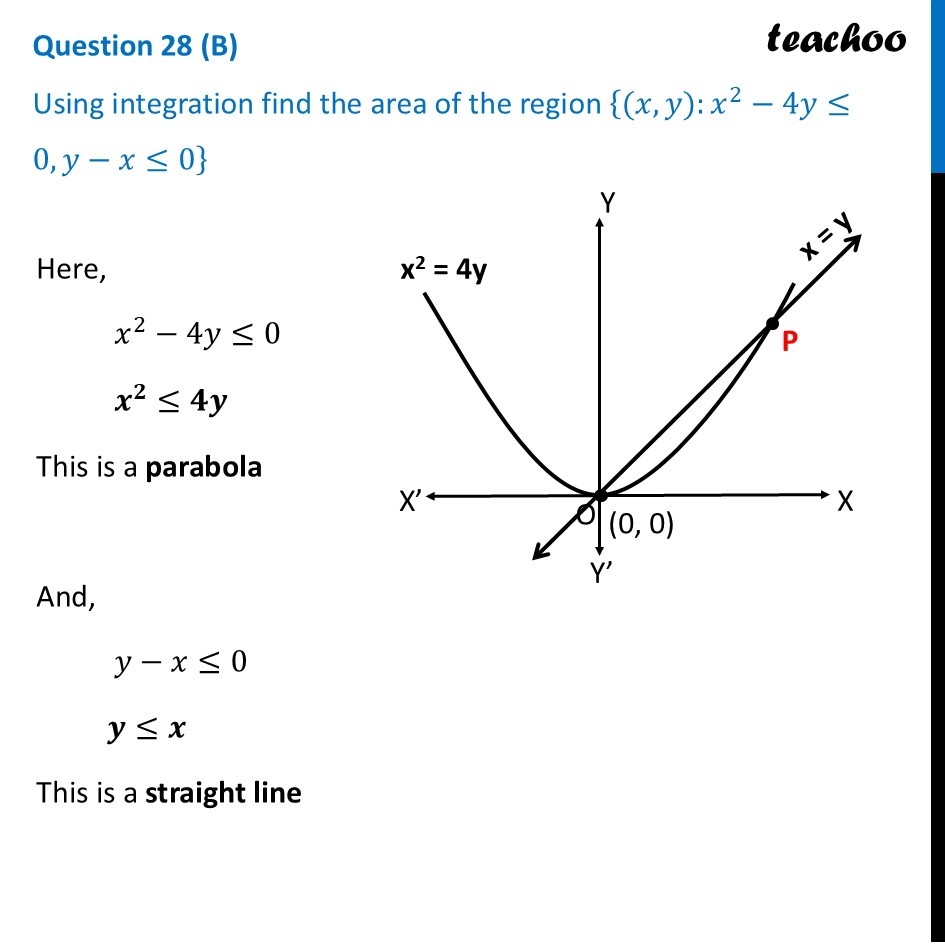
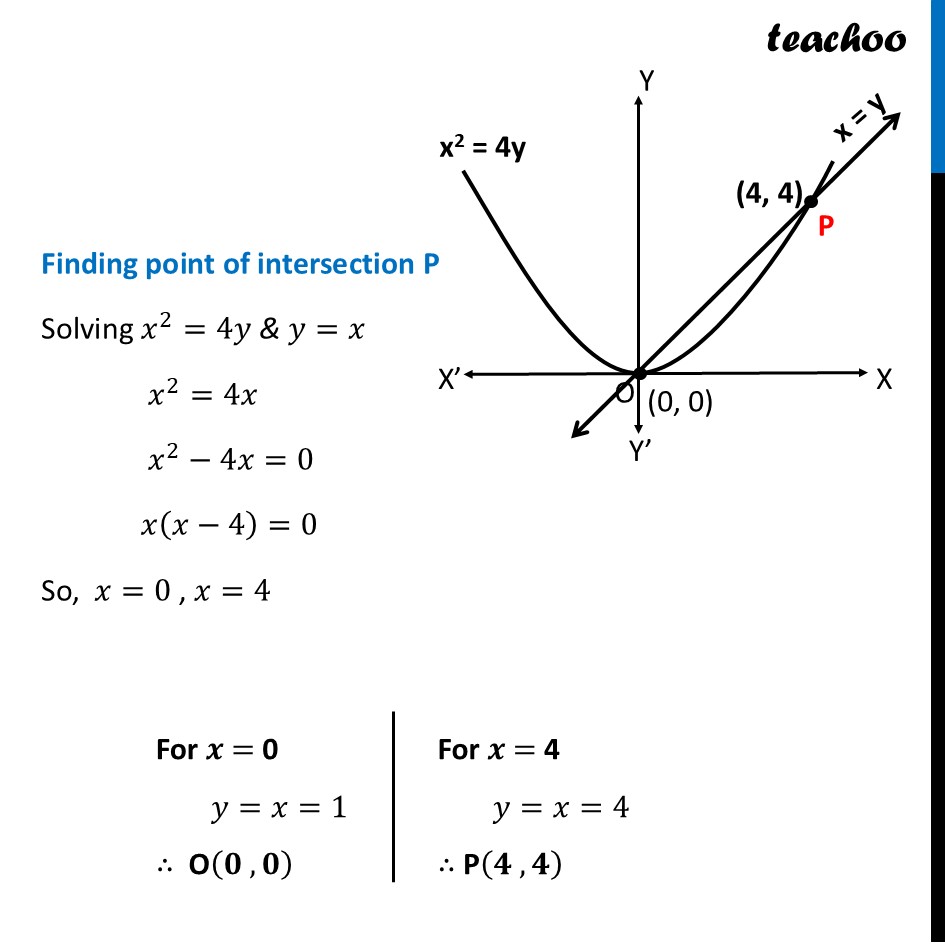
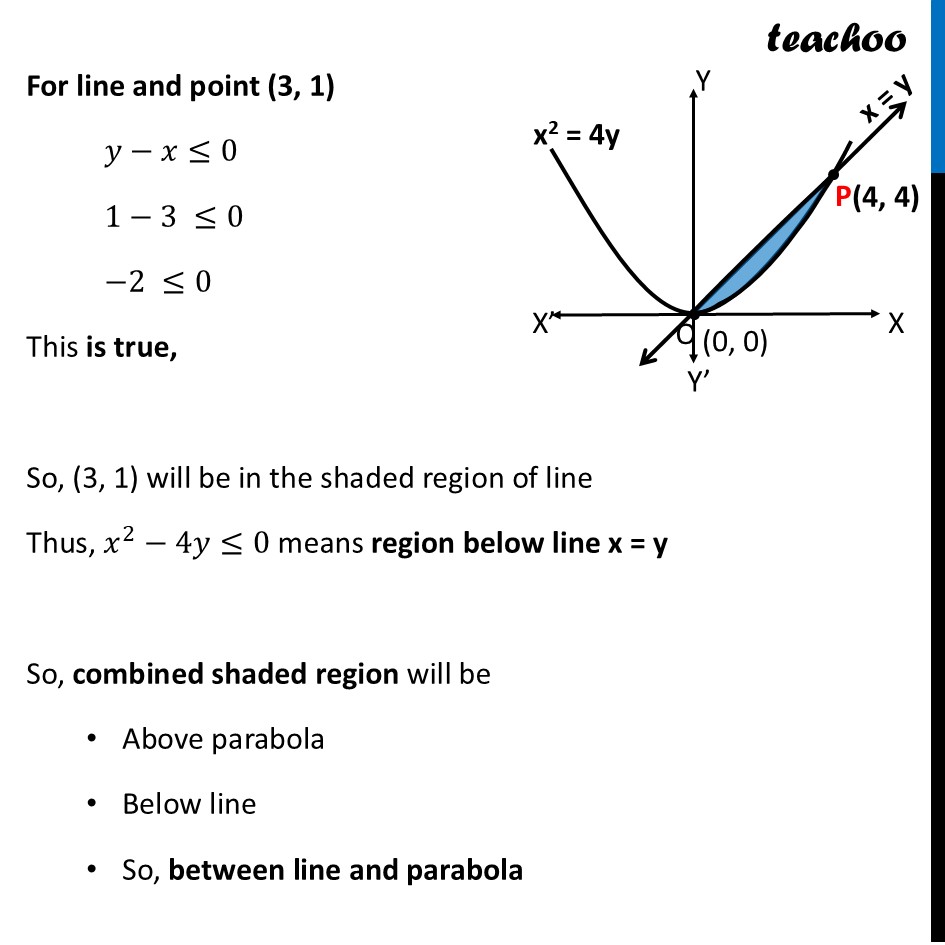
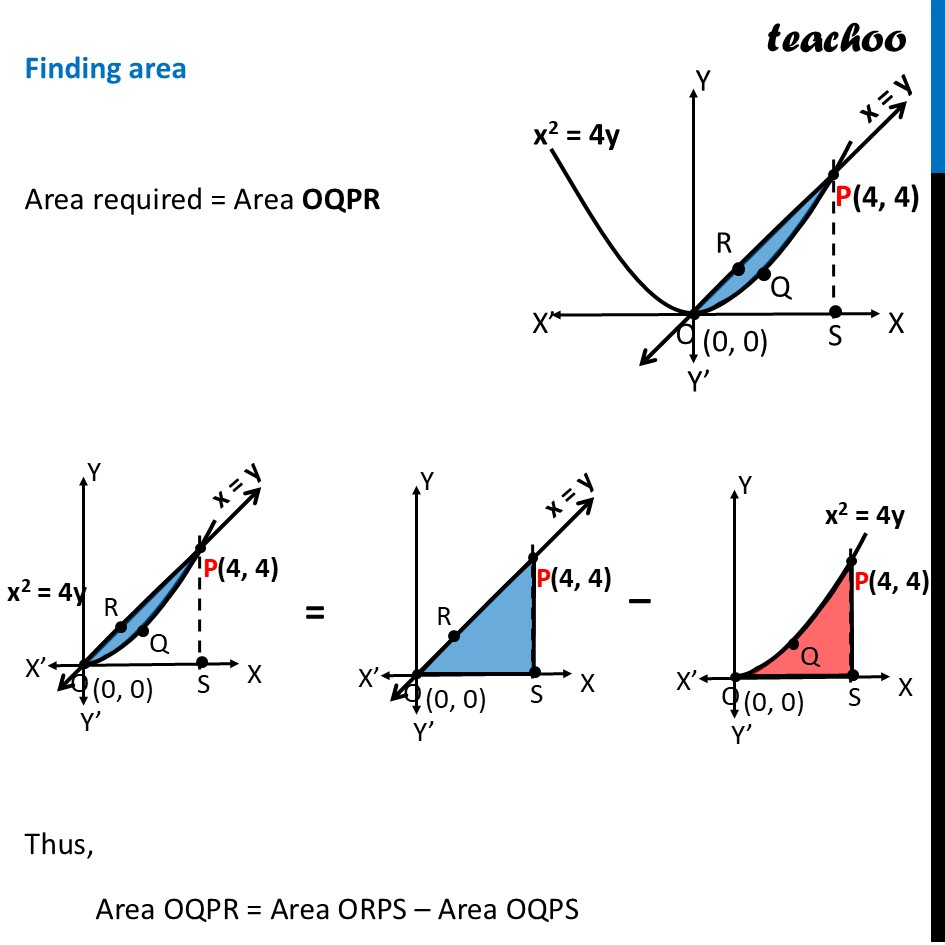
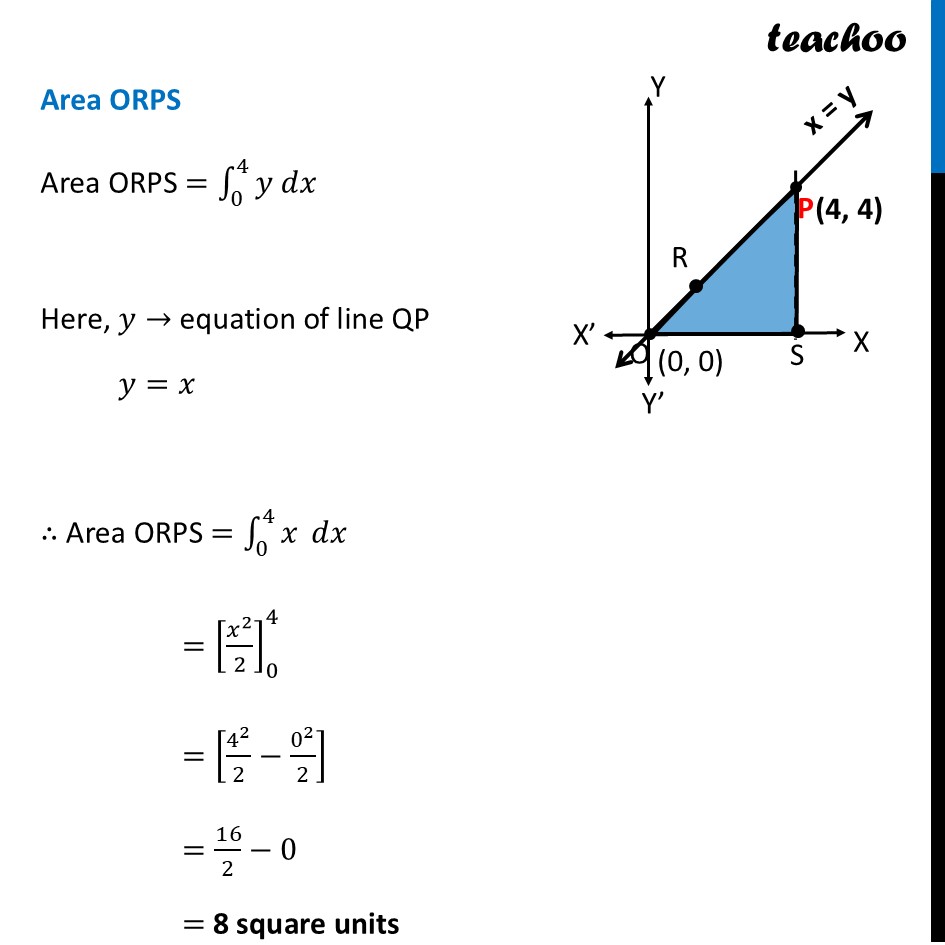
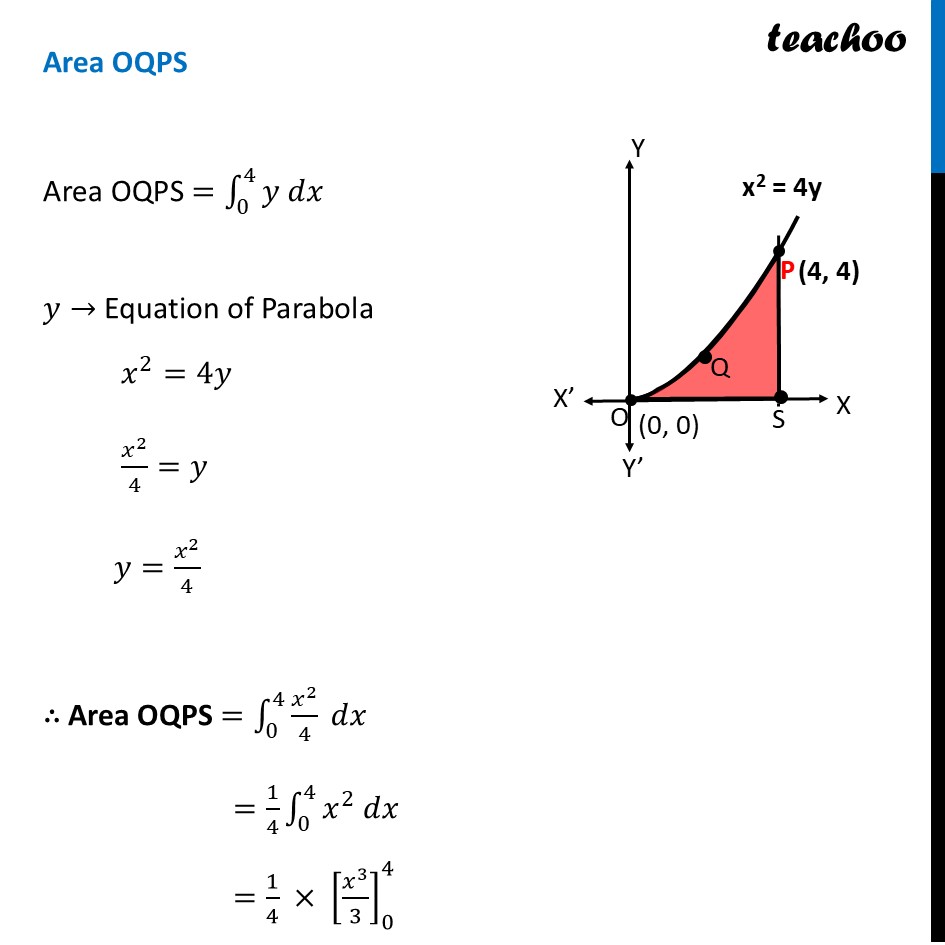
Question 28 (B) Using integration find the area of the region {(𝑥,𝑦):𝑥^2−4𝑦≤0,𝑦−𝑥≤0}Here, 𝑥^2−4𝑦≤0 𝒙^𝟐≤𝟒𝒚 This is a parabola And, 𝑦−𝑥≤0 𝒚≤𝒙 This is a straight line Finding point of intersection P Solving 𝑥^2=4𝑦 & 𝑦=𝑥 𝑥^2=4𝑥 𝑥^2−4𝑥=0 𝑥(𝑥−4)=0 So, 𝑥=0 , 𝑥=4 For 𝒙 = 0 𝑦=𝑥=1 ∴ O(𝟎 , 𝟎) For 𝒙 = 4 𝑦=𝑥=4 ∴ P(𝟒 , 𝟒) Finding Area to be shaded Now, our region is {(𝑥,𝑦):𝑥^2−4𝑦≤0,𝑦−𝑥≤0} Let’s take point (3, 1) – which is below parabola and line For parabola and point (3, 1) 𝑥^2−4𝑦≤0 3^2−4(1) ≤0 9−5 ≤0 4 ≤0 This is not true, So, (3, 1) will not be in the shaded region of parabola Thus, 𝑥^2−4𝑦≤0 means region above parabola x2 = 4y For line and point (3, 1) 𝑦−𝑥≤0 1−3 ≤0 −2 ≤0 This is true, So, (3, 1) will be in the shaded region of line Thus, 𝑥^2−4𝑦≤0 means region below line x = y So, combined shaded region will be Above parabola Below line So, between line and parabola Finding area Area required = Area OQPR Thus, Area OQPR = Area ORPS – Area OQPS Area ORPS Area ORPS =∫_0^4▒〖𝑦 𝑑𝑥〗 Here, 𝑦→ equation of line QP 𝑦=𝑥 ∴ Area ORPS =∫_0^4▒𝑥 𝑑𝑥 =[𝑥^2/2]_0^4 =[4^2/2−0^2/2] =16/2−0 = 8 square units Area OQPS Area OQPS =∫_0^4▒〖𝑦 𝑑𝑥〗 𝑦→ Equation of Parabola 𝑥^2=4𝑦 𝑥^2/4=𝑦 𝑦=𝑥^2/4 ∴ Area OQPS =∫_0^4▒〖𝑥^2/4 𝑑𝑥〗 =1/4 ∫_0^4▒〖𝑥^2 𝑑𝑥〗 =1/4 × [𝑥^3/3]_0^4 =1/4 × [4^3/3−0^3/3] =4^2/3 =𝟏𝟔/𝟑 square units Thus, Area Required = Area ORPS – Area OQPS = 8−16/3 = (8 × 3 − 16)/3 = (24 − 16)/3 = 𝟖/𝟑 square units