CBSE Class 12 Sample Paper for 2026 Boards
You are here
CBSE Class 12 Sample Paper for 2026 Boards
Last updated at September 2, 2025 by Teachoo
This question is similar to Chapter 8 Class 12 Application of Integrals - Ex 8.1
Please check the question here
Β
![[SPQ 12] Find out the area of shaded region in the enclosed figure - CBSE Class 12 Sample Paper for 2026 Boards](https://cdn.teachoo.com/c64cb239-446c-40d0-82d2-5ba714ed5bc0/slide13.jpg)
Transcript
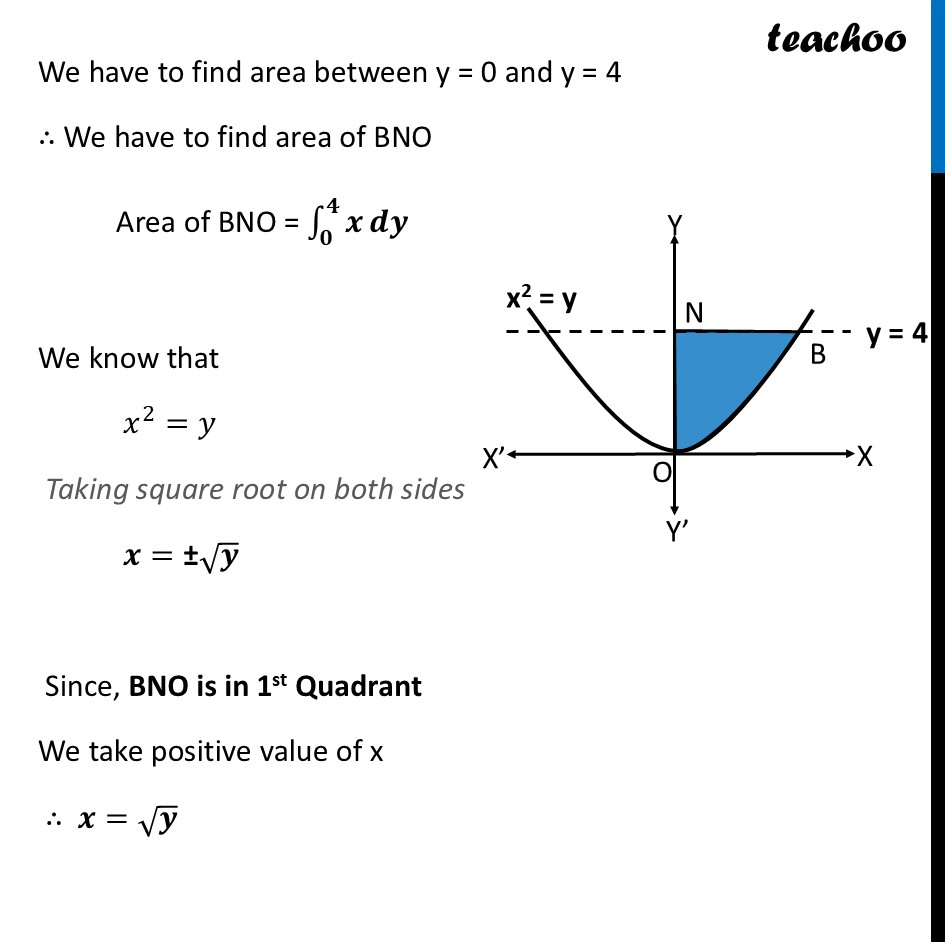
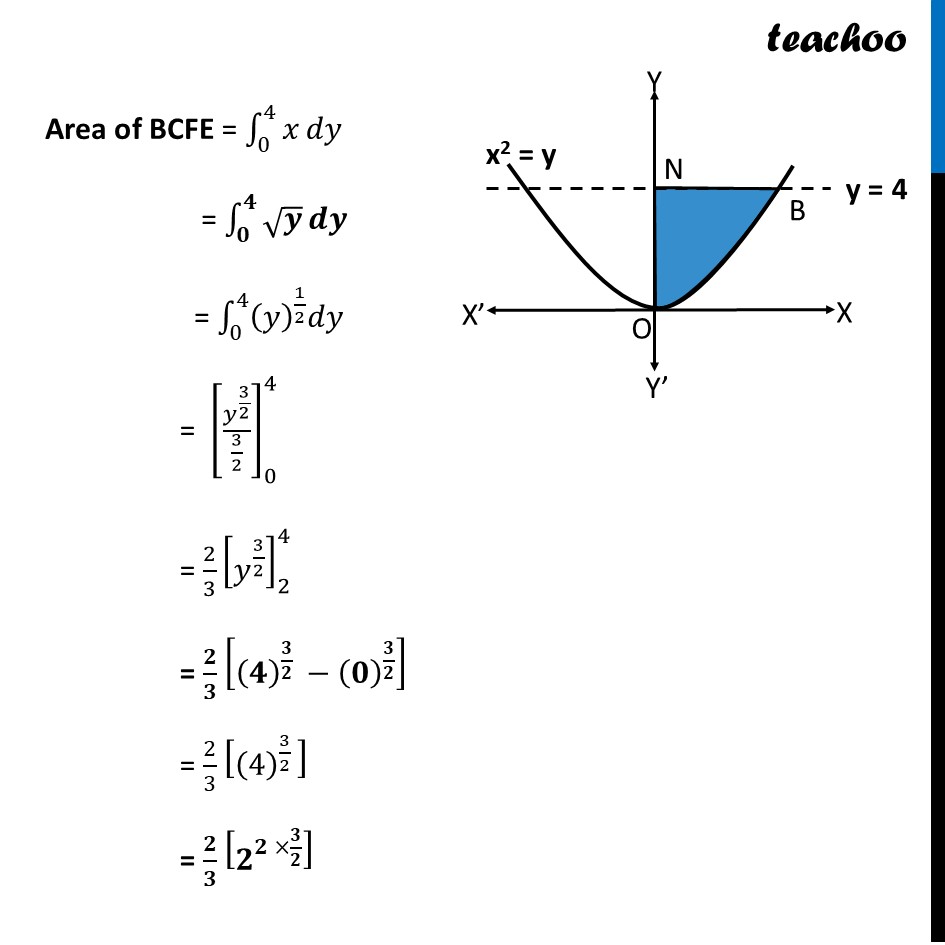
Question 23 (B) Find out the area of shaded region in the enclosed figure. Letβs redraw the figure The curve is π^π=π We have to find area between y = 0 and y = 4 β΄ We have to find area of BNO Area of BNO = β«_π^πβπ π π We know that π₯^2=π¦ Taking square root on both sides π="Β±" βπ Since, BNO is in 1st Quadrant We take positive value of x β΄ π=βπ Area of BCFE = β«_0^4βπ₯ ππ¦ = β«_π^πββπ π π = β«_0^4βγ(π¦)^(1/2) ππ¦γ = [π¦^(3/2)/(3/2)]_0^4 = 2/3 [π¦^(3/2) ]_2^4 = π/π [(π)^(π/π )β(π)^(π/π) ] = 2/3 [(4)^(3/2 ) ] = π/π [π^(π Γπ/π) ] = 2/3 Γ 2^3 = (2 Γ 8)/3 = ππ/π Thus, Area = ππ/π square units Area of BCFE = β«_0^4βπ₯ ππ¦ = β«_π^πββπ π π = β«_0^4βγ(π¦)^(1/2) ππ¦γ = [π¦^(3/2)/(3/2)]_0^4 = 2/3 [π¦^(3/2) ]_2^4 = π/π [(π)^(π/π )β(π)^(π/π) ] = 2/3 [(4)^(3/2 ) ] = π/π [π^(π Γπ/π) ]
