Question 9 - The value of 𝛼 if angle between 𝑝⃗ = 2𝛼2𝑖̂ − 3𝛼𝑗̂ +

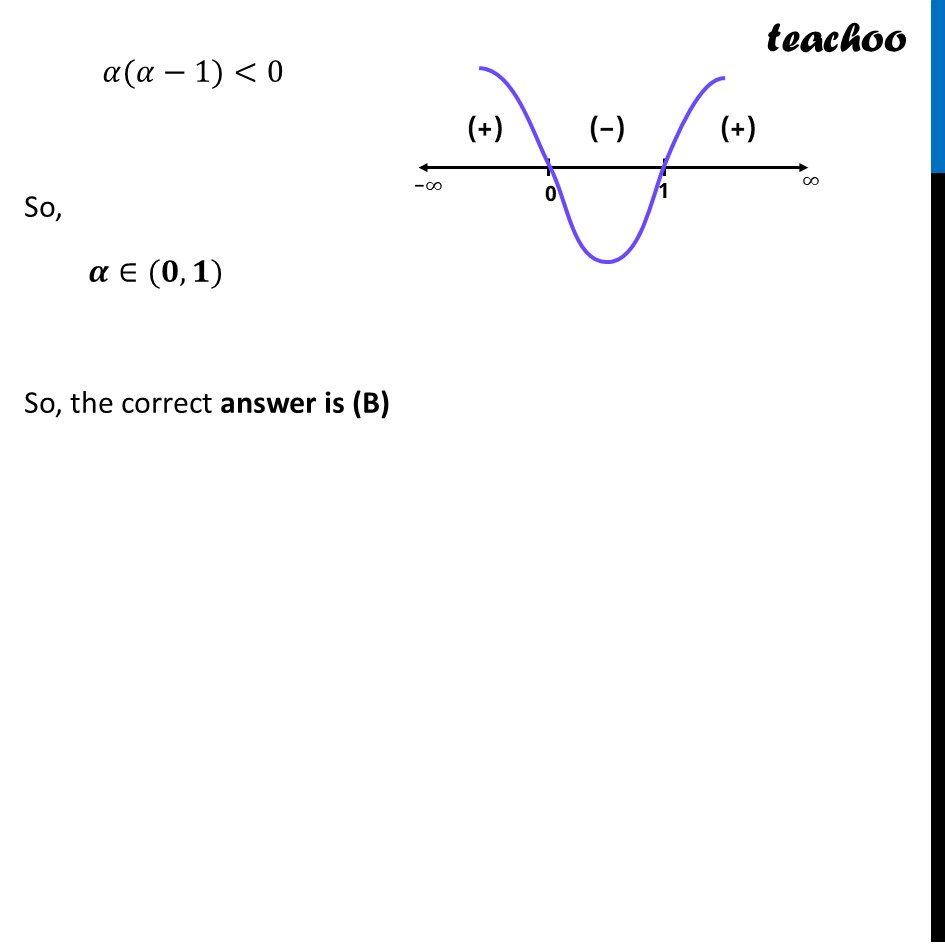
Question 9 The value of 𝛼 if the angle between 𝑝 ⃗=2𝛼^2 ı ˆ−3𝛼ȷ ˆ+𝑘 ˆ and 𝑞 ⃗=ı ˆ+ȷ ˆ+𝛼𝑘 ˆ is obtuse, is (A) 𝑅−[0,1] (B) (0,1) (C) [0,∞) (D) [1,∞) Angle between two vectors is found using dot product We know that 𝑝 ⃗ . 𝑞 ⃗ = "|" 𝑝 ⃗"|" "|" 𝑞 ⃗"|" cos θ cos θ = (𝒑 ⃗" . " 𝒒 ⃗)/(|𝒑 ⃗ |" " |𝒒 ⃗|) where θ is the angle between 𝑝 ⃗ and 𝑞 ⃗ Since angle between 𝑝 ⃗ and 𝑞 ⃗ is obtuse cos θ < 0 Putting values (𝑝 ⃗" . " 𝑞 ⃗)/(|𝑝 ⃗ |" " |𝑞 ⃗|)<0 Since "|" 𝑝 ⃗"|" "|" 𝑞 ⃗"|" is a number, we can multiply it to right side 𝑝 ⃗" . " 𝑞 ⃗<0 ×|𝑝 ⃗ |" "|𝑞 ⃗| 𝒑 ⃗" . " 𝒒 ⃗<𝟎 (2𝛼^2 ı ˆ−3𝛼ȷ ˆ+𝑘 ˆ ).(ı ˆ+ȷ ˆ+𝛼𝑘 ˆ )<0 2𝛼^2 × 1−3𝛼 × 1+1 × 𝛼<0 2𝛼^2 −3𝛼+ 𝛼<0 2𝛼^2 −2𝛼<0 2𝛼(𝛼−1)<0 𝜶(𝜶−𝟏)<𝟎 So, the correct answer is (B) 𝛼(𝛼−1)<0 So, 𝜶∈(𝟎, 𝟏) So, the correct answer is (B)

Question 9 - CBSE Class 12 Sample Paper for 2025 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular