Ex 6.3,23 - Chapter 6 Class 12 Application of Derivatives

Transcript

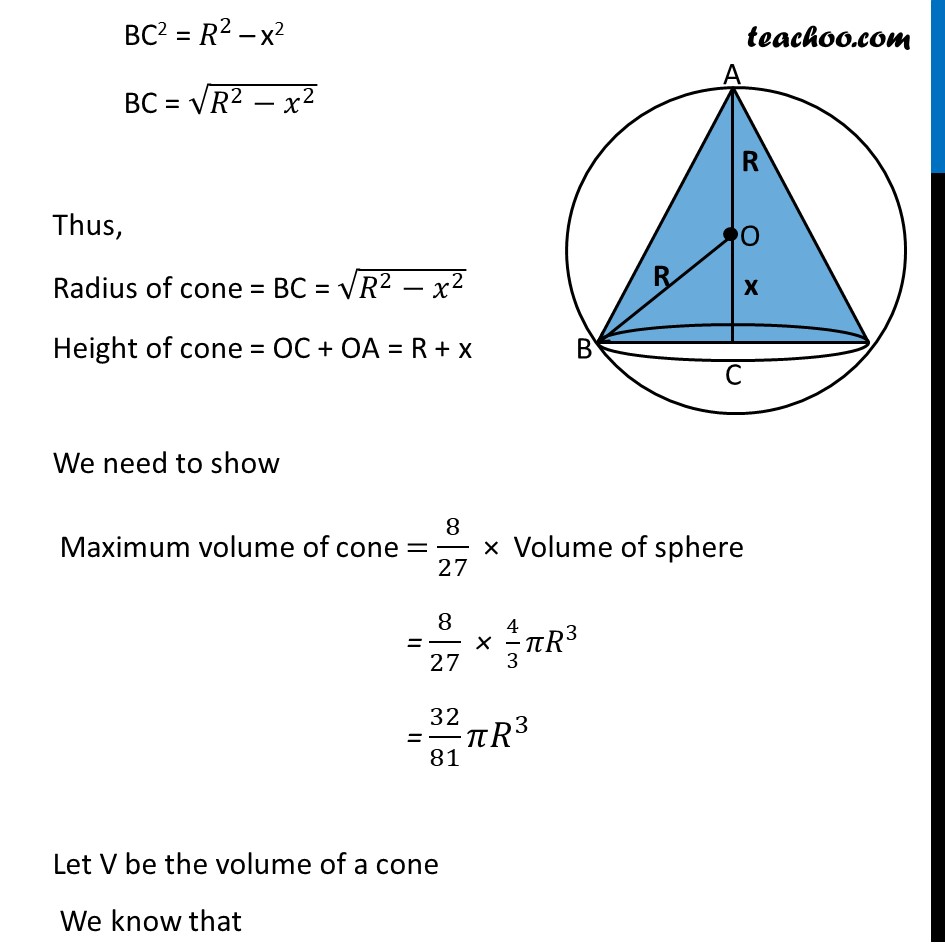
Ex 6.3, 23 Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.Cone of largest volume inscribed in the sphere of radius R Let OC = x Radius of cone = BC Height of cone = h = OC + OA Finding OC Δ BOC is a right angled triangle Using Pythagoras theorem in ∆BOC 〖𝑂𝐵〗^2=〖𝐵𝐶〗^2+〖𝑂𝐶〗^2 R2 =〖𝐵𝐶〗^2+𝑥^2 BC2 = 𝑅^2 – x2 BC = √(𝑅^2−𝑥^2 ) Thus, Radius of cone = BC = √(𝑅^2−𝑥^2 ) Height of cone = OC + OA = R + x We need to show Maximum volume of cone = 8/27 × Volume of sphere = 8/27 × 4/3 𝜋𝑅^3 = 32/81 𝜋𝑅^3 Let V be the volume of a cone We know that Volume of a cone = 1/3 𝜋(𝑟𝑎𝑑𝑖𝑢𝑠 )^2 (ℎ𝑒𝑖𝑔ℎ𝑡 ) V = 1/3 𝜋(√(𝑅^2−𝑥^2 ))^2 (𝑅+𝑥) V = 1/3 𝜋(𝑅^2−𝑥^2 )(𝑅+𝑥) V = 1/3 𝜋(𝑅^2 (𝑅+𝑥)−𝑥^2 (𝑅+𝑥)) V = 1/3 𝜋(𝑅^(3 )+𝑅^2 𝑥−𝑥^2 𝑅−𝑥^3 ) Diff w.r.t 𝒙 𝑑𝑉/𝑑𝑥=𝑑/𝑑𝑥 [1/3 𝜋(𝑅^(3 )+𝑅^2 𝑥−𝑥^2 𝑅−𝑥^3 )] 𝑑𝑉/𝑑𝑥=𝜋/3 [𝑑/𝑑𝑥 (𝑅^(3 )+𝑅^2 𝑥−𝑥^2 𝑅−𝑥^3 )] 𝑑𝑉/𝑑𝑥=𝜋/3 (0+𝑅^2.1−𝑅 ×2𝑥−3𝑥^2 ) 𝑑𝑉/𝑑𝑥=𝜋/3 (𝑅^2−2𝑅𝑥−3𝑥^2 ) Putting 𝒅𝑽/𝒅𝒙=𝟎 1/3 𝜋(𝑅^2−2𝑅𝑥−3𝑥^2 )=0 𝑅^2−2𝑅𝑥−3𝑥^2=0 𝑅^2−3𝑅𝑥+𝑅𝑥−3𝑥^2=0 R(𝑅−3𝑥)+𝑥(𝑅−3𝑥)=0 (𝑅+𝑥)(𝑅−3𝑥)=0 So, x = –R & 𝑥=𝑅/3 Since x cannot be negative 𝑥=𝑅/3 Finding (𝒅^𝟐 𝒗)/(𝒅𝒙^𝟐 ) 𝑑𝑣/𝑑𝑥=1/3 𝜋(𝑅^2−2𝑅𝑥−3𝑥^2 ) (𝑑^2 𝑣)/(𝑑𝑥^2 )=𝜋/3 𝑑/𝑑𝑥 (𝑅^2−2𝑅𝑥−3𝑥^2 ) (𝑑^2 𝑣)/(𝑑𝑥^2 )=𝜋/3 (0−2𝑅−6𝑥) (𝑑^2 𝑣)/(𝑑𝑥^2 )=(−𝜋)/3 (2𝑅+6𝑥) Putting 𝒙=𝑹/𝟑 〖(𝑑^2 𝑣)/(𝑑𝑥^2 )│〗_(𝑥 = 𝑅/3) =(−𝜋)/3 (2𝑅+6(𝑅/3)) =(−𝜋)/3 (2𝑅+2𝑅) =(−𝜋)/3 (4𝑅) =(−4𝜋𝑅)/3 < 0 Thus (𝑑^2 𝑣)/(𝑑𝑥^2 )<0 when 𝑥=𝑅/3 ∴ Volume is Maximum when 𝑥=𝑅/3 Finding maximum volume From (1) Volume of cone = 1/3 𝜋(𝑅^2−𝑥^2 )(𝑅+𝑥) Putting 𝑥 = 𝑅/3 = 1/3 𝜋(𝑅^2−(𝑅/3)^2 )(𝑅+𝑅/3) = 1/3 𝜋(𝑅^2−𝑅^2/9)((3𝑅 + 𝑅)/3) = 1/3 𝜋((9𝑅^2− 𝑅^2)/9)(4𝑅/3) = 𝟑𝟐/𝟖𝟏 𝝅𝑹^𝟑 Hence proved