Ex 9.2, 18 - Chapter 9 Class 11 Straight Lines

Transcript

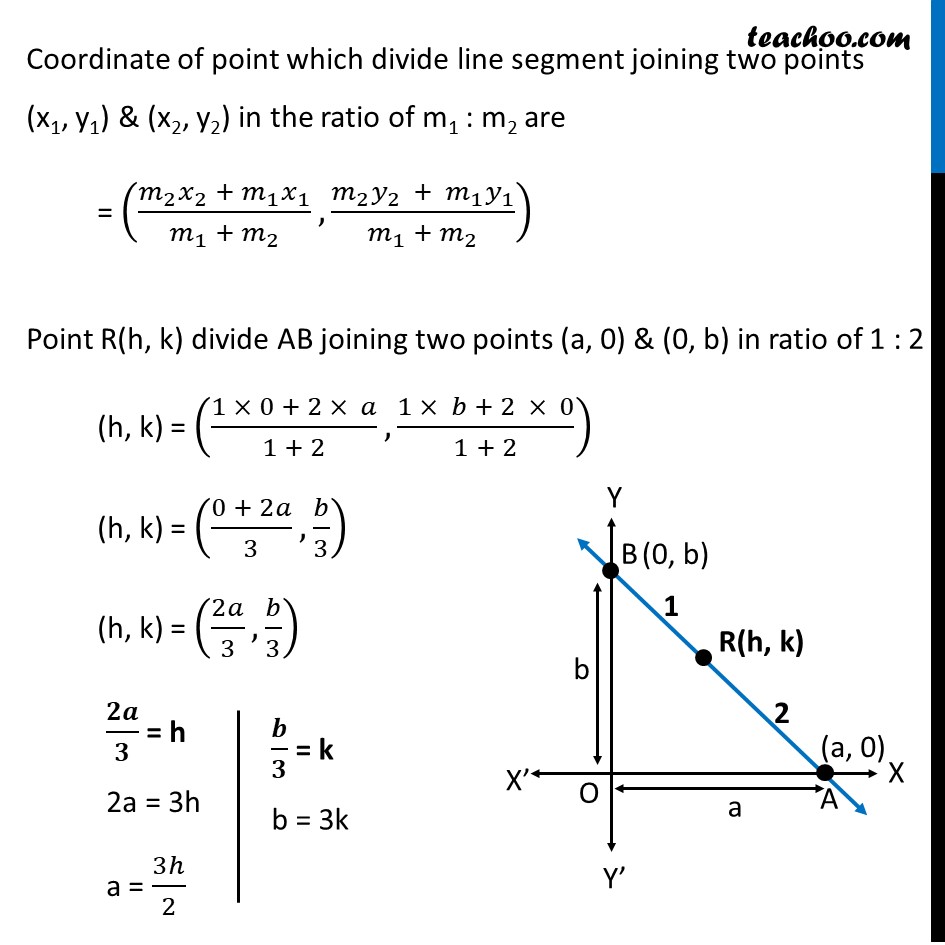
Ex 9.2, 18 Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find equation of the line. Let the AB be a line between axis & point R(h, k) divides AB in the ratio 1: 2 Let AB make x-intercept a & y-intercept b Point A = (a, 0) & B = (0, b) So, equation of line AB by intercept form is 𝑥/𝑎 + (𝑦 )/𝑏 = 1 Coordinate of point which divide line segment joining two points (x1, y1) & (x2, y2) in the ratio of m1 : m2 are = ((𝑚_2 𝑥_2 + 𝑚_1 𝑥_1)/(𝑚_1 + 𝑚_2 ),(𝑚_2 𝑦_(2 ) + 𝑚_1 𝑦_1)/(𝑚_1 + 𝑚_2 )) Point R(h, k) divide AB joining two points (a, 0) & (0, b) in ratio of 1 : 2 (h, k) = ((1 × 0 + 2 × 𝑎)/(1 + 2), (1 × 𝑏 + 2 × 0)/(1 + 2)) (h, k) = ((0 + 2𝑎)/3, 𝑏/3) (h, k) = (2𝑎/3, 𝑏/3) 𝟐𝒂/𝟑 = h 2a = 3h a = 3ℎ/2 𝒃/𝟑 = k b = 3k Putting value of a & b in (1) 𝑥/𝑎 + (𝑦 )/𝑏 = 1 𝑥/(3ℎ/2) + (𝑦 )/3𝑘 = 1 2𝑥/3ℎ + (𝑦 )/3𝑘 = 1 1/3 (2𝑥/ℎ+ (𝑦 )/𝑘) = 1 (2𝑥(𝑘) + 𝑦(ℎ))/ℎ𝑘 = 1 × 3 (2𝑘𝑥 + ℎ𝑦)/(ℎ𝑘 ) = 3 2kx + hy = 3hk Which is the required equation