Ex 9.2, 14 - Chapter 9 Class 11 Straight Lines

Transcript

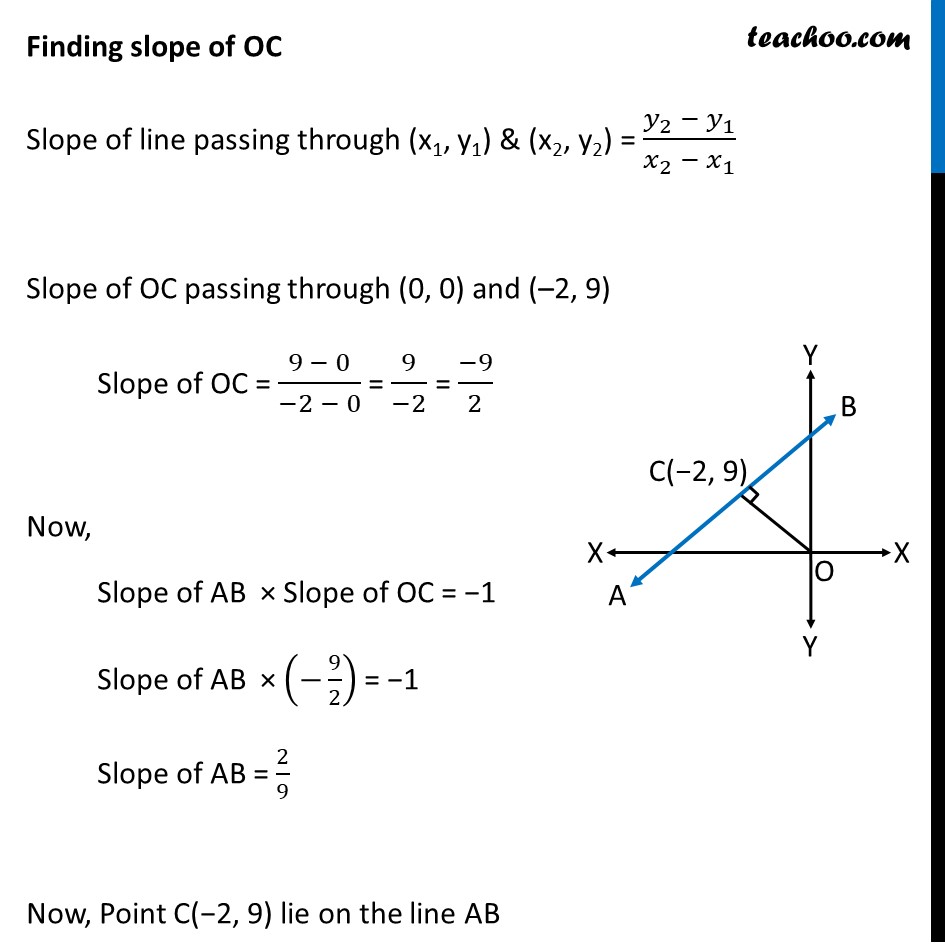
Ex 9.2, 14 The perpendicular from the origin to a line meets it at the point (– 2, 9), find the equation of the line. Let line OC be perpendicular to line AB at point C (–2, 9) i.e. OC perpendicular AB We know that If two lines are perpendicular then product of their slopes is equal to −1 ∴ Slope of OC × Slope of AB = −1 Finding slope of OC Slope of line passing through (x1, y1) & (x2, y2) = (𝑦_2 − 𝑦_1)/(𝑥_2 − 𝑥_1 ) Slope of OC passing through (0, 0) and (–2, 9) Slope of OC = (9 − 0)/(−2 − 0) = 9/(−2) = (−9)/2 Now, Slope of AB × Slope of OC = −1 Slope of AB × (−9/2) = −1 Slope of AB = 2/9 Now, Point C(−2, 9) lie on the line AB Hence line AB passes through C(−2, 9) with slope 2/9 We know that equation of line passing through (x0, y0) & having slope m is (y – y0) = m (x – x0) Equation of line AB passing through (−2, 9)& having slope 2/9 (y – 9) = 2/9 (x – (−2)) y – 9 = 2/9 (x + 2) 9(y – 9) = 2(x + 2) 9y – 81 = 2x + 4 9y – 2x – 81 – 4 = 0 9y – 2x – 85 = 0 0 = 2x – 9y + 85 2x – 9y + 85 = 0 Which is the required equation of AB