Ex 11.2, 3 - Chapter 11 Class 12 Three Dimensional Geometry

Transcript

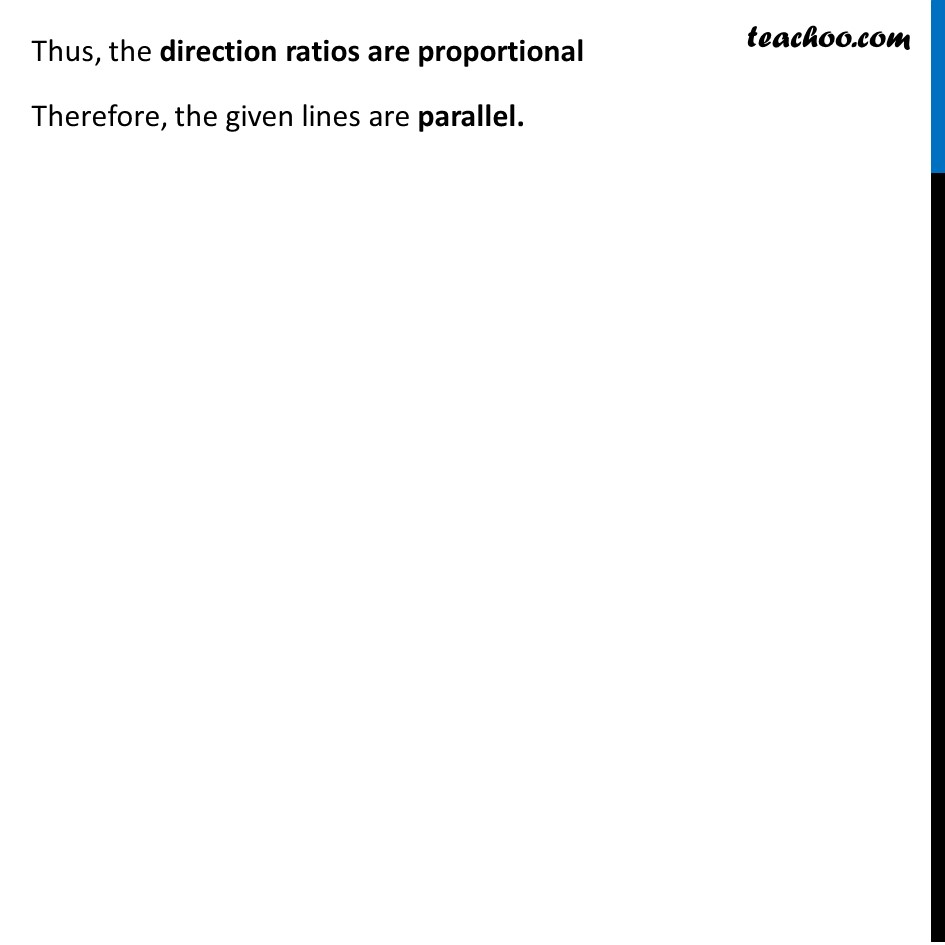
Ex 11.2, 3 Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).Two lines having direction ratios 𝑎1, b1, c1 and 𝑎2, b2, c2 are parallel if 𝒂𝟏/𝒂𝟐 = 𝒃𝟏/𝒃𝟐 = 𝒄𝟏/𝒄𝟐 Also, a line passing through (x1, y1, z1) and (x2, y2, z2) has the direction ratios (x2 − x1), (y2 − y1), (z2 − z1) A (4, 7, 8), B (2, 3, 4) Direction ratios = 2 − 4, 3 − 7, 4 − 8 = −2, −4, −4 ∴ 𝒂𝟏 = −2, 𝒃𝟏 = −4, 𝒄𝟏 = −4 C (−1, −2, 1), D (1, 2, 5) Direction ratios = 1 − (−1), 2 − (−2), 5 − 1 = 2, 4, 4 ∴ 𝒂𝟐 = 2, 𝒃𝟐 = 4, 𝒄𝟐 = 4 Now, 𝒂𝟏/𝒂𝟐 = (−2)/2 = –1 𝒃𝟏/𝒃𝟐 = (−4)/4 = –1 𝒄𝟏/𝒄𝟐 = (−4)/4 = –1 Since 𝑎1/𝑎2 = 𝑏1/𝑏2 = 𝑐1/𝑐2 = −1 Thus, the direction ratios are proportional Therefore, the given lines are parallel.