If 𝑥^𝑦=𝑒^(𝑥−𝑦) prove that 𝑑𝑦/𝑑𝑥=(log 𝑥)/((log (𝑥𝑒))^2 )

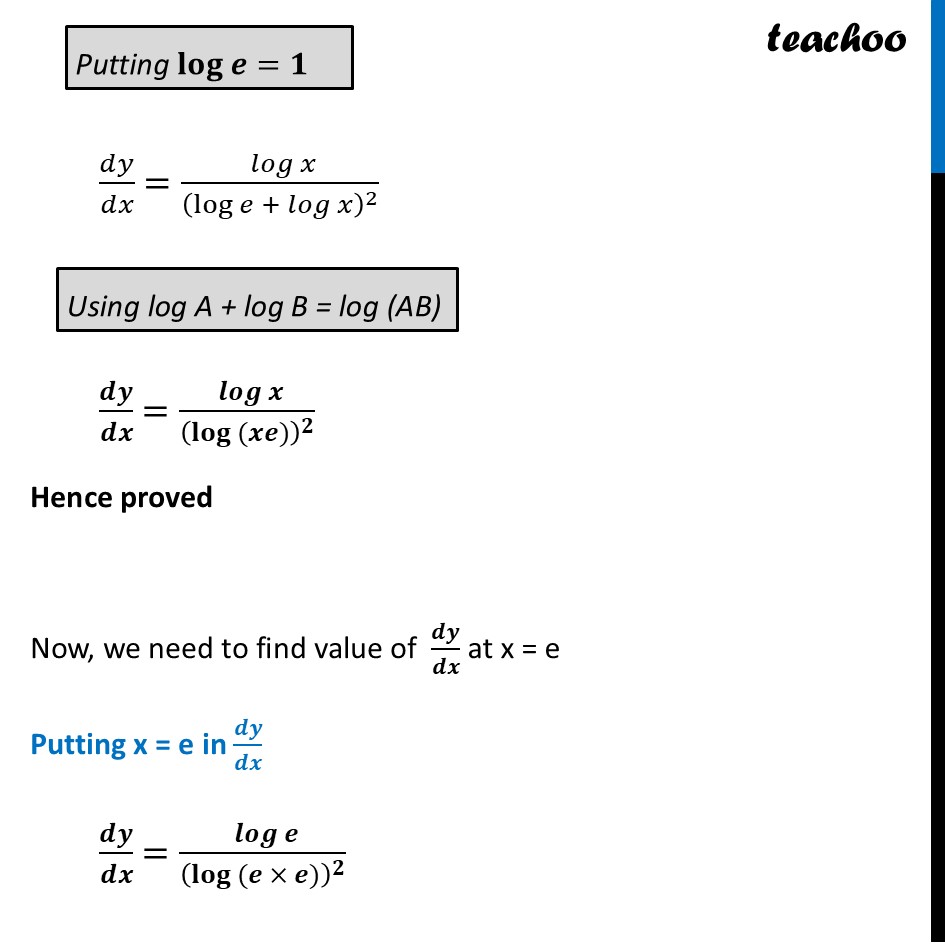
Question 26 (A) If 𝑥^𝑦=𝑒^(𝑥−𝑦) prove that 𝑑𝑦/𝑑𝑥=(log 𝑥)/((log (𝑥𝑒))^2 ) and hence find its value at 𝑥=𝑒.Given, 𝑥^𝑦=𝑒^(𝑥−𝑦) Taking log both sides log (𝑥^𝑦 ) = log (𝑒^(𝑥 − 𝑦) ) 𝑦 × log 𝑥=(𝑥−𝑦) × log⁡𝑒 𝒚 × 𝐥𝐨𝐠 𝒙=(𝒙−𝒚) Differentiating both sides 𝑤.𝑟.𝑡.𝑥. 𝑑(𝑦.〖 log〗⁡𝑥 )/𝑑𝑥=(𝑑(𝑥 − 𝑦))/𝑑𝑥 (As 𝑙𝑜𝑔⁡(𝑎^𝑏 )=𝑏 . 𝑙𝑜𝑔⁡𝑎) (Since 𝑙𝑜𝑔⁡𝑒=1) Using product Rule As (𝑢𝑣)’ = 𝑢’𝑣 + 𝑣’𝑢 𝑑(𝑦)/𝑑𝑥 " ". log 𝑥 + 𝑑(log⁡𝑥 )/𝑑𝑥 . 𝑦 =𝑑(𝑥)/𝑑𝑥−(𝑑(𝑦))/𝑑𝑥 𝒅𝒚/𝒅𝒙 𝒍𝒐𝒈 𝒙 + 𝟏/𝒙 . 𝒚 =𝟏−𝒅𝒚/𝒅𝒙 𝑑𝑦/𝑑𝑥 log 𝑥 + 𝑦/𝑥 =1−𝑑𝑦/𝑑𝑥 𝑑𝑦/𝑑𝑥 log 𝑥 + 𝑑𝑦/𝑑𝑥 =1−𝑦/𝑥 𝒅𝒚/𝒅𝒙 (𝒍𝒐𝒈 𝒙+𝟏) =((𝒙 − 𝒚)/𝒙) Since 𝒚 𝐥𝐨𝐠 𝒙=(𝒙−𝒚) 𝑦 𝑙𝑜𝑔 𝑥+𝑦=𝑥 𝑥=𝑦 𝑙𝑜𝑔 𝑥+𝑦 𝒙=𝒚 (𝟏+ 𝐥𝐨𝐠 𝒙) 𝑑𝑦/𝑑𝑥 (𝑙𝑜𝑔 𝑥+1) =(𝒚(𝟏 + 𝒍𝒐𝒈 𝒙) − 𝑦)/(𝒚(𝟏 + 𝒍𝒐𝒈 𝒙)) 𝑑𝑦/𝑑𝑥 (𝑙𝑜𝑔 𝑥+1) =(𝑦 + 𝑦𝑙𝑜𝑔 𝑥 − 𝑦)/(𝑦(1 + 𝑙𝑜𝑔 𝑥)) 𝑑𝑦/𝑑𝑥 (𝑙𝑜𝑔 𝑥+1) =( 𝑦𝑙𝑜𝑔 𝑥)/(𝑦(1 + 𝑙𝑜𝑔 𝑥)) 𝑑𝑦/𝑑𝑥 (𝑙𝑜𝑔 𝑥+1) =( 𝑙𝑜𝑔 𝑥)/((1 + 𝑙𝑜𝑔 𝑥)) 𝒅𝒚/𝒅𝒙 =( 𝒍𝒐𝒈 𝒙)/(𝟏 + 𝒍𝒐𝒈 𝒙)^𝟐 𝑑𝑦/𝑑𝑥 =( 𝑙𝑜𝑔 𝑥)/(log⁡𝑒 + 𝑙𝑜𝑔 𝑥)^2 𝒅𝒚/𝒅𝒙 =( 𝒍𝒐𝒈 𝒙)/(〖𝐥𝐨𝐠 〗⁡〖(𝒙𝒆〗))^𝟐 Hence proved Now, we need to find value of 𝒅𝒚/𝒅𝒙 at x = e Putting x = e in 𝒅𝒚/𝒅𝒙 𝒅𝒚/𝒅𝒙 =( 𝒍𝒐𝒈 𝒆)/(〖𝐥𝐨𝐠 〗⁡〖(𝒆 × 𝒆〗))^𝟐 𝑑𝑦/𝑑𝑥 =( 𝑙𝑜𝑔 𝑒)/(〖𝑙𝑜𝑔 〗⁡〖(𝑒^2 〗))^2 𝑑𝑦/𝑑𝑥 =( 𝑙𝑜𝑔 𝑒)/(2 × 〖𝑙𝑜𝑔 〗⁡𝑒 )^2 𝑑𝑦/𝑑𝑥 =1/(2 × 1)^2 𝑑𝑦/𝑑𝑥 =1/2^2 𝒅𝒚/𝒅𝒙 =𝟏/𝟒

Question 26 (A) - CBSE Class 12 Sample Paper for 2026 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular