The two vectors ı ˆ+ȷ ˆ+𝑘 ˆ and (3ı) ̂−ȷ ˆ+3𝑘 ˆ represent the two

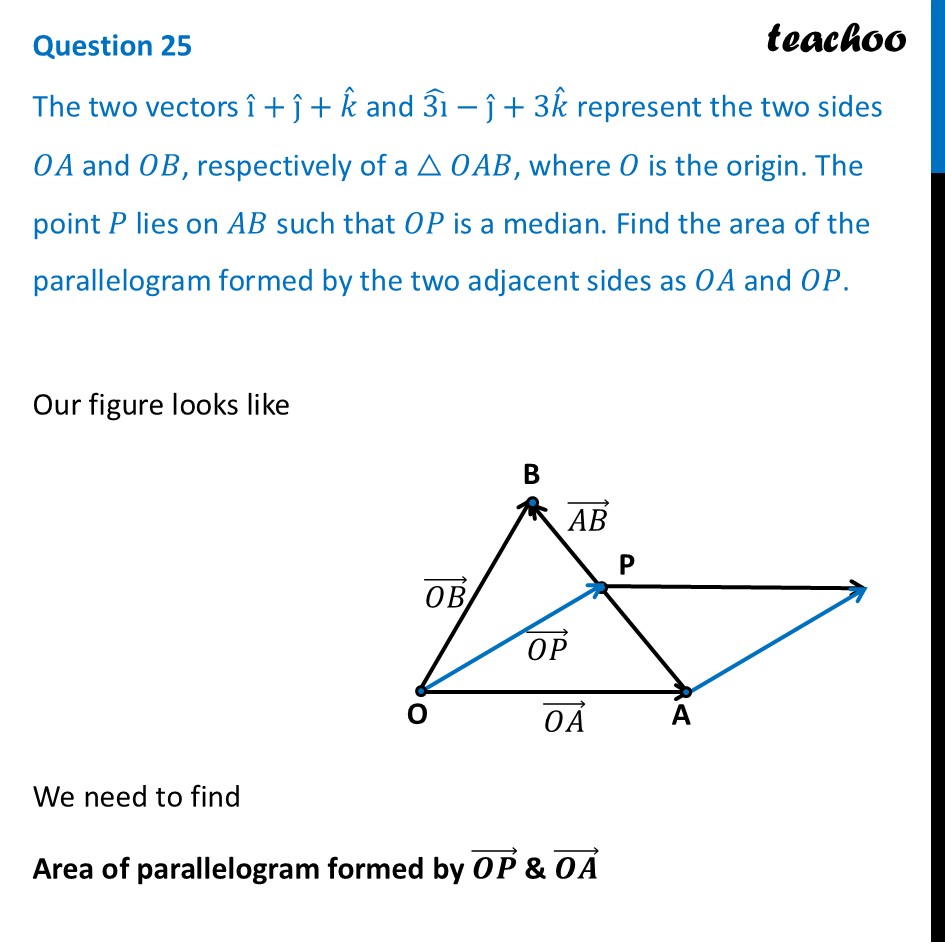
Question 25 The two vectors ı ˆ+ȷ ˆ+𝑘 ˆ and (3ı) ̂−ȷ ˆ+3𝑘 ˆ represent the two sides 𝑂𝐴 and 𝑂𝐵, respectively of a △𝑂𝐴𝐵, where 𝑂 is the origin. The point 𝑃 lies on 𝐴𝐵 such that 𝑂𝑃 is a median. Find the area of the parallelogram formed by the two adjacent sides as 𝑂𝐴 and 𝑂𝑃.Our figure looks like We need to find Area of parallelogram formed by (𝑶𝑷) ⃗ & (𝑶𝑨) ⃗ We need to find (𝑂𝑃) ⃗ first Finding (𝑶𝑷) ⃗ (𝑶𝑷) ⃗ is the position vector of Point P Since point P is mid-point of AB Position vector of P = ((𝑶𝑨) ⃗ + (𝑶𝑩) ⃗)/𝟐 (𝑂𝑃) ⃗ = ((𝑖 ̂ + 𝑗 ̂ + 𝑘 ̂ ) + (3𝑖 ̂ − 𝑗 ̂ + 3𝑘 ̂))/2 (𝑂𝑃) ⃗ = ((1 + 3) 𝑖 ̂ + (1 − 1) 𝑗 ̂ + (1 + 3)𝑘 ̂)/2 (𝑂𝑃) ⃗ = (4𝑖 ̂ + 4𝑘 ̂)/2 (𝑂𝑃) ⃗ = (2(2𝑖 ̂ + 2𝑘 ̂))/2 (𝑂𝑃) ⃗ = 𝟐𝒊 ̂+𝟐𝒌 ̂ = √8 = 𝟐√𝟐 Area of parallelogram = |(𝑂𝑃) ⃗ × (𝑂𝐴) ⃗ | = 𝟐√𝟐 square units Therefore, the required area is 𝟐√𝟐 square units Finding Area of parallelogram made by (𝑶𝑷) ⃗ & (𝑶𝑨) ⃗ Area of parallelogram = |(𝑂𝑃) ⃗ × (𝑂𝐴) ⃗ | Now, (𝑶𝑷) ⃗ × (𝑶𝑨) ⃗ = |■8(𝑖 ̂&𝑗 ̂&𝑘 ̂@2&0&2@1&1&1)| = 𝑖 ̂ (0 × 1 – 1 × 2) − 𝑗 ̂ (2 × 1 – 1 × 2) + 𝑘 ̂ (2 × 1 − 1 × 0) = –2𝑖 ̂ − 𝑗 ̂ × 0 + 2𝑘 ̂ = –2𝒊 ̂ + 2𝒌 ̂ Magnitude of (𝑶𝑷) ⃗ × (𝑶𝑨) ⃗ = √((−2)2+(2)2) |(𝑶𝑷) ⃗ × (𝑶𝑨) ⃗ | = √(4+4)

Question 25 - CBSE Class 12 Sample Paper for 2026 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Davneet Singh

Class 6

Class 7

Class 8

Class 9

Class 10

Class 11

Class 12

Courses

Interesting

Popular